A block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
mg2m+M
2mgm+M
mgm+M
2mg2m+M
The correct Answer is:D
To find the acceleration of the block when released, we can follow these steps:
Step 1: Identify the Forces Acting on the Block
The forces acting on the block of mass m are:
- The gravitational force acting downward, which is mg.
- The tension T in the string acting upward.
Using Newton's second law, we can write the equation of motion for the block:
\( mg - T = ma \)
where a is the acceleration of the block.
Step 2: Analyze the Pulley
The pulley has a mass M and a radius R. The tension in the string creates a torque on the pulley. The torque τ due to the tension is given by:
\( τ = T \cdot R \)
The moment of inertia I of the pulley (assuming it's a solid disk) is:
\( I = \frac{1}{2} M R^2 \)
Using the relation between torque and angular acceleration, we have:
\( τ = I \cdot \alpha \)
where α is the angular acceleration of the pulley. Since the string does not slide over the pulley, the linear acceleration a of the block is related to the angular acceleration α of the pulley by:
\( a = R \cdot \alpha \)
Thus, we can express α as:
\( α = \frac{a}{R} \)
Step 3: Write the Equation for the Pulley
Substituting the expressions for torque and moment of inertia into the torque equation gives:
\( T \cdot R = \frac{1}{2} M R^2 \cdot \frac{a}{R} \)
Simplifying this, we get:
\( T = \frac{1}{2} M a \)
Step 4: Substitute Tension into the Block's Equation
Now we have two equations:
1. From the block: \( mg - T = ma \)
2. From the pulley: \( T = \frac{1}{2} M a \)
Substituting the expression for T from the pulley into the block's equation:
\( mg - \frac{1}{2} M a = ma \)
Step 5: Solve for Acceleration
Rearranging the equation gives:
\( mg = ma + \frac{1}{2} M a \)
\( mg = a \left( m + \frac{1}{2} M \right) \)
Now, solving for a:
\( a = \frac{mg}{m + \frac{1}{2} M} \)
Final Result
Thus, the acceleration of the block when released is:
\( a = \frac{mg}{m + \frac{1}{2} M} \)
---
The forces acting on the block of mass m are:
- The gravitational force acting downward, which is mg.
- The tension T in the string acting upward.
\( mg - T = ma \)
where a is the acceleration of the block.
The pulley has a mass M and a radius R. The tension in the string creates a torque on the pulley. The torque τ due to the tension is given by:
\( τ = T \cdot R \)
\( I = \frac{1}{2} M R^2 \)
\( τ = I \cdot \alpha \)
where α is the angular acceleration of the pulley. Since the string does not slide over the pulley, the linear acceleration a of the block is related to the angular acceleration α of the pulley by:
\( a = R \cdot \alpha \)
Thus, we can express α as:
\( α = \frac{a}{R} \)
Substituting the expressions for torque and moment of inertia into the torque equation gives:
\( T \cdot R = \frac{1}{2} M R^2 \cdot \frac{a}{R} \)
Simplifying this, we get:
\( T = \frac{1}{2} M a \)
Now we have two equations:
1. From the block: \( mg - T = ma \)
2. From the pulley: \( T = \frac{1}{2} M a \)
\( mg - \frac{1}{2} M a = ma \)
Rearranging the equation gives:
\( mg = ma + \frac{1}{2} M a \)
\( mg = a \left( m + \frac{1}{2} M \right) \)
Now, solving for a:
\( a = \frac{mg}{m + \frac{1}{2} M} \)
Thus, the acceleration of the block when released is:
\( a = \frac{mg}{m + \frac{1}{2} M} \)
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Solved Examples
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.1
6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
A block of mass m hangs by means of a string which goes over a pulley of mass m and moment of inertia l, as shown in the diagram. The string does not relative to the pulley. Find the frequency of small oscillations.
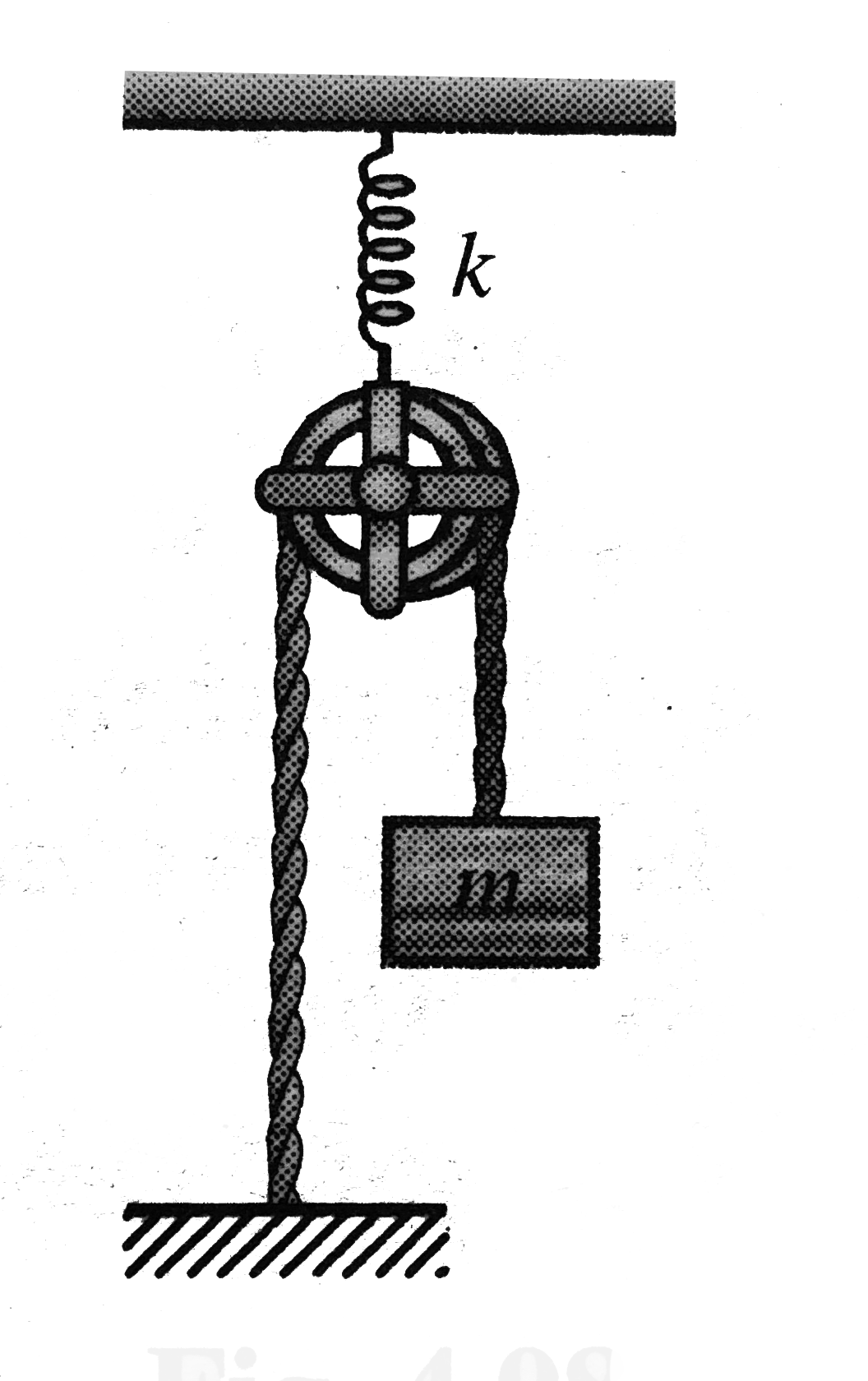
View SolutionTwo masses 2m and m are attached to the ends of the card which passes over a pulley of mass m and radius R. Calculate the tension in the wire on both sides of the pulley. Assume no slipping.
View Solution
Knowledge Check
A block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
Amg2m+MB2mgm+MCmgm+MD2mg2m+MThe ratio of acceleration of pulley to the acceleration of the block is (string is inextensible).
 A0.5B2C1DNone of these
A0.5B2C1DNone of theseTwo masses M1=5kg,M2=10kg are connected at the ends of an inextensible string passing over a frictionless pulley as shown. When masses are released, then acceleration of masses will be
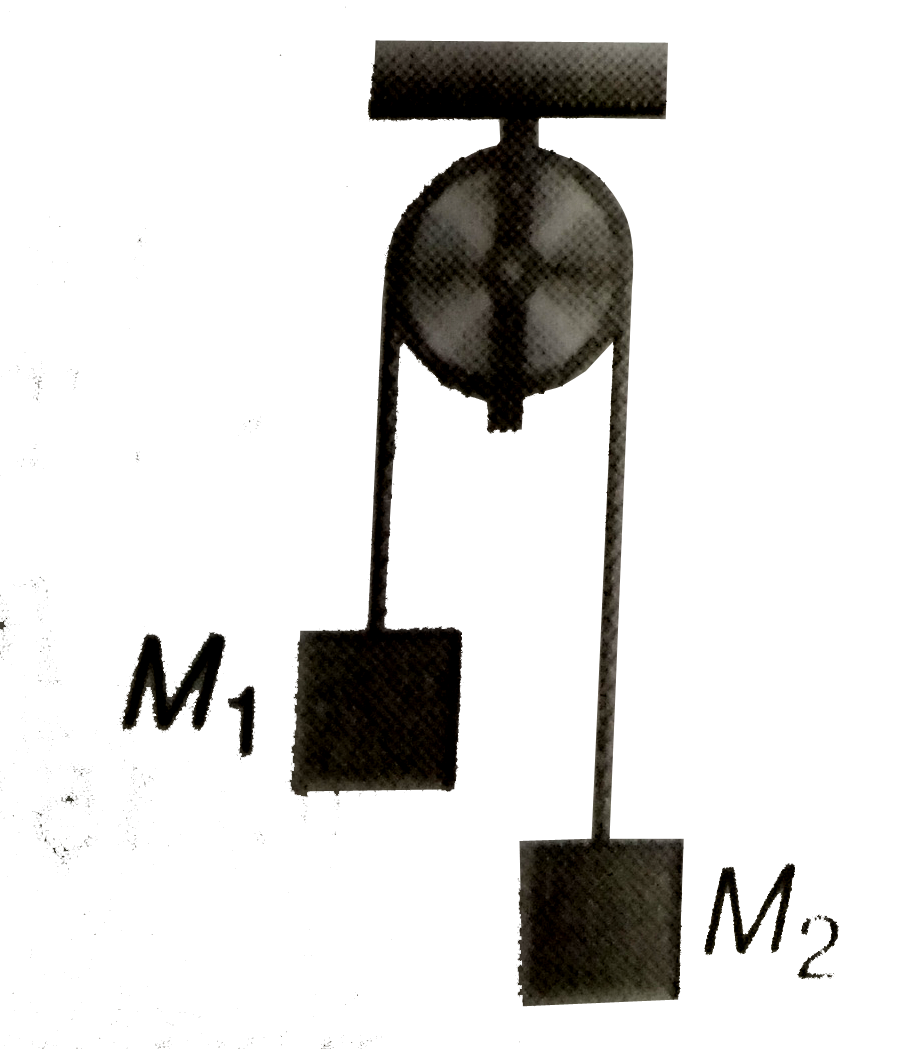 AgBg/2Cg/3Dg/4
AgBg/2Cg/3Dg/4
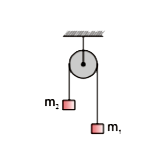
Two blocks of masses m1 and m2 are attached at the ends of an inextensible string which passes over a smooth massless pulley. If m1>m2, find :
(i) the acceleration of each block
(ii) the tension in the string.
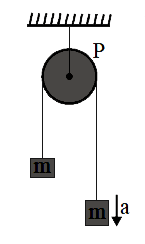
View SolutionIn the figure, the blocks unequal masses m1 and m2 (m1<m2).m2 has a downward acceleration a. The pulley P has a radius r, and some mass. The string does not slip on the pulley. Find the acceleration of block and angular acceleration of pulley. (I = momentum of inerita of pulley)
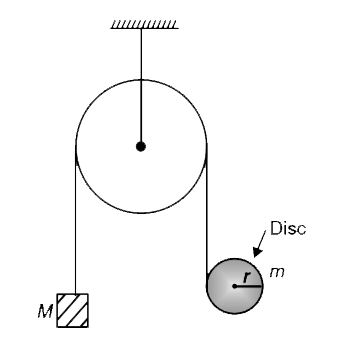
View SolutionA mass less string is wrapped around a uniform disc of mass m and radius r. The string passes over a mass less pulley and is tied to a block of mass M at its other end (see figure). The system is released from rest. Assume that the string does not slip with respect to the disc.
(a) Find the acceleration of the block for the case M=m
(b) Find Mm for which the block can accelerate upwards.
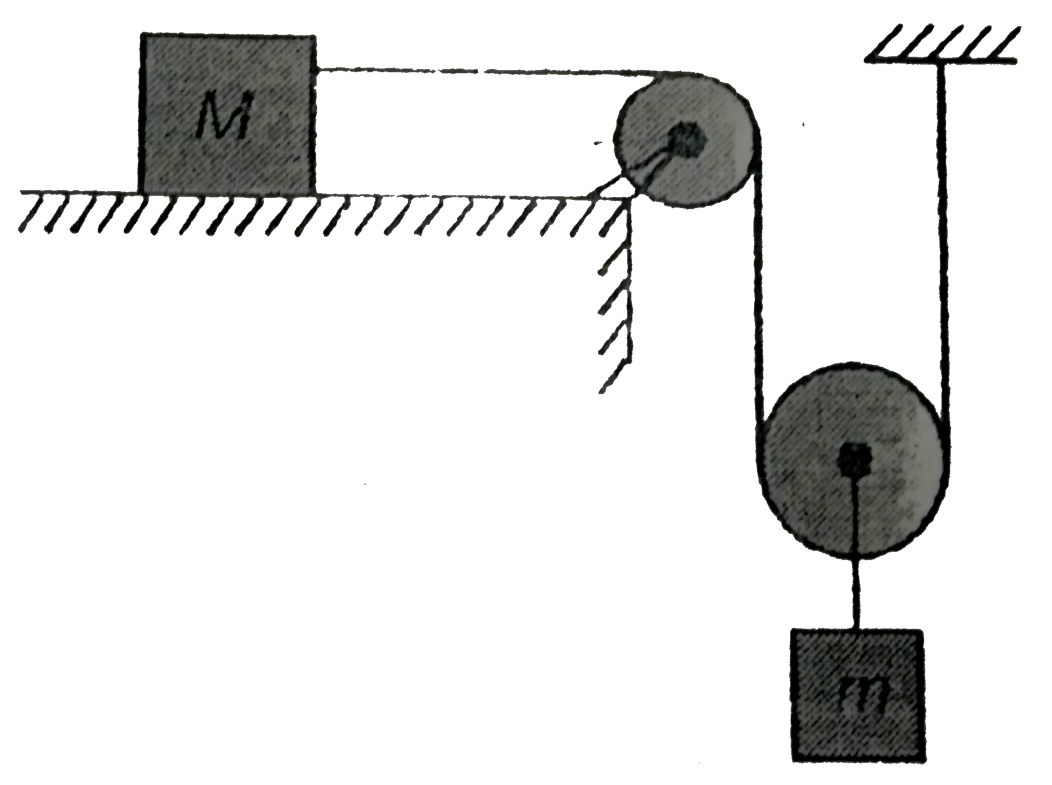
View SolutionA block of mass M is placed on a horizontal surface. It is tied with an inextensible string that passes through ideal pulleys. A mass m is connected to the pulley as shown. For what value of m, the block M will accelerate towards the fixed pulley ?
View SolutionA uniform solid cylinder of mass M and radius 2R rests on a horizontal table top. A string attached to it runs over a pulley (disc) of mass M and radius R thatis mounted on a frictionless axle through its centre. A block of mass M is suspended from the free end of the string. The string doesn't slip over the pulley surface, and the cylinder rolls without slipping on the, table top. Find the acceleration of the block.

[g/3]
View Solution
