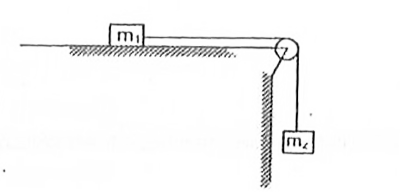
Two blocks of masses m1 and m2 are attached at the ends of an inextensible string which passes over a smooth massless pulley. If m1>m2, find :
(i) the acceleration of each block
(ii) the tension in the string.
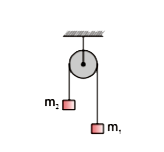
The block m1 is assumed to be moving downward and the block m2 is assumed to be moving upward, It is merely an assumption and it does not imply the real direction. If the values of a1 and a2 come out to be positive then body the assumed directions are correct, oherwise the body moves in the opposite direction. Since the pulley is smoth and massless, therefore, the tension on each side of the pulley is same. The free body diagram of each block is shown in the figure.
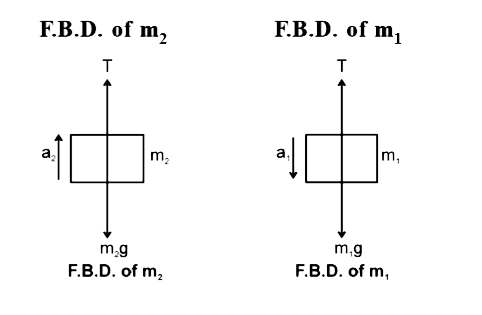
Fig. 1.1
Applying Newton's second Law on blocks m1 and m2
Block m1 m1g−T=m1a.........(1)
Block m2 −m2g+T=m2a2...........(2)
Number of unknowns : T, a1 and a2 (three)
Number of equations : only two
Obviously, we require one more equation to solve the problem Note that whenever one finds the number of equations less than the number of unknowns, one must think about the constraint relation. Now we are going to explain the mathematical procedure for this.
How to determine Constraint Relation ?
(1) Assume the direction of acceleration of each block e.g. a1 (downward) and a2 (upward) in this case.
(2) Locate the position of each block from a fixed point (depending on convenience), e.g. centre of the pulley in this case.
(3) Identify the constraint and write down the equation of constraint in terms of the distance assumed. For example, in the chosen problem, the length of string remains constant is the constraint or restriction.
Thus, x1+x2= constant
we get dx1dt+dx2dt=0
Each term on the left side represents the velocity of the blocks. Since we have to find a relation between acceletations, therefore we differntiate it once again w.r.t. time.

Thus d2x1dt2+d2x2dt2=0
Since, the block m1 is assumed to be moving downward (x1 is increasing with timw)
∴d2x1dt2=+a1
and block m2 is assumed to be moving upward (x2 is decreasing with time)
∴d2x2dt2=−a2
Thus a1−a2=0
or a1=a2=a (say) is the required constraint relation. Substituting a1=a2=a in equations (1) and (2) and solving them, we get
(i)a=[m1−m2m1+m2]g (ii) T=[2m1m2m1+m2]g
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - NEWTON'S LAWS OF MOTION & FRICTION EXERCISE - Problem26videos
NEWTON'S LAWS OF MOTION & FRICTION
- BOOK - MOTIONCHAPTER - NEWTON'S LAWS OF MOTION & FRICTION EXERCISE - Questions For Practice25videos
NEWTON'S LAWS OF MOTION & FRICTION
- BOOK - MOTIONCHAPTER - MODERN PHYSICS -1EXERCISE - EXERCISE-4 ( LEVEL- II)39videos
MODERN PHYSICS -1
- BOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - EXERCISE-4 ( LEVEL-II)15videos
NLM & FRICTION
Similar Questions
Two masses M and m are connected at the two ends of an inextensible string. The string passes over a smooth frictionless pulley. Calculate the acceleration of the masses and the tension in the string. Given M>m.
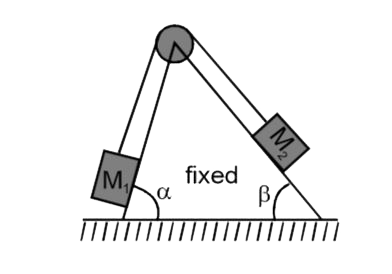
View SolutionTwo masses M1 and M2 are attached to the ends of a light string which passes over a massless pulley attached to the top of a double inclined smooth plane of angles of inclination α and β.The tension in the string is :
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
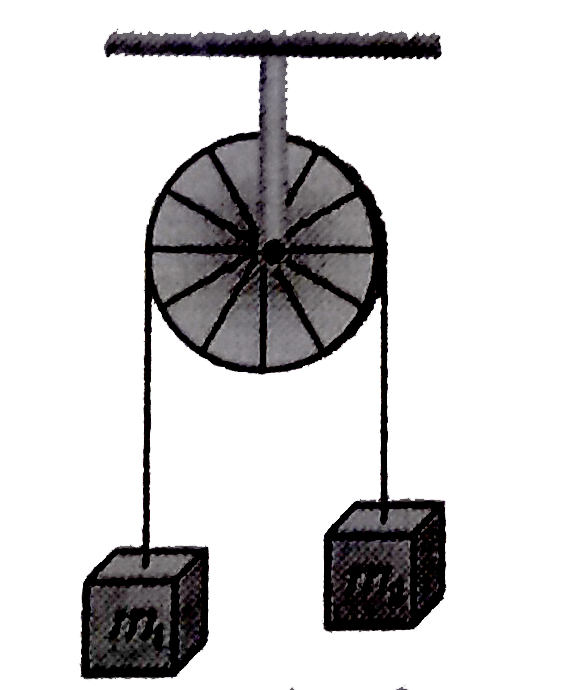
Two masses m1 and m2 are attached to a string which passes over a frictionless smooth pulley. When m1=10kg,m2=6kg, the acceleration of masses is
 A20m/s2B5m/s2C2.5m/s2D10m/s2
A20m/s2B5m/s2C2.5m/s2D10m/s2 - Question 2 - Select One
Two bodies of masses m1 and m2 are connected a light string which passes over a frictionless massless pulley. If the pulley is moving upward with uniform acceleration g2, then tension in the string will be
A3m1m2m1+m2gBm1+m24m1m2gC2m1m2m1+m2gDm1m2m1+m2g - Question 3 - Select One
Two blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
Ag, vertically downwardsBg5, vertically downwardsCg25, vertically downwardsDzero
Two masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.
View SolutionTwo mass m1andm2 are attached to a flexible inextensible massless rope, which passes over a frictionless and massless pully. Find the accelerations of the masses and tension in the rope.
 View Solution
View SolutionA block of mass m1=2 kg is kept on a smooth horizontal table. Another block of mass m2=1 kg is connected to m1 by a light inextensible string passing over a smooth pulley as shown in the figure. If the blocks are released, what will be the (a) acceleration of each block (b) tension in the string?
 View Solution
View SolutionTwo blocks are connected by an inextensible light string, the string is passing over smooth, light pulley as shown. Find the acceleration of blocks and tension in the string, reaction in pulley.
 View Solution
View SolutionTwo blocks of masses m1=4kg and m2=2kg are connected to the ends of a string which passes over a massless, frictionless pulley. The total downwards thrust on the pulley is nearly
 View Solution
View Solution

