A block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R figure a. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
To find the acceleration of the block when released, we can follow these steps:
Step 1: Identify the forces acting on the block
When the block of mass m is released, the forces acting on it are:
- The gravitational force downward: \( F_g = mg \)
- The tension in the string acting upward: \( T \)
Step 2: Write the equation of motion for the block
Using Newton's second law for the block, we can write:
\(
mg - T = ma \tag{1}
\)
where \( a \) is the acceleration of the block downward.
Step 3: Analyze the pulley
The pulley has a mass \( M \) and radius \( R \). The tension in the string creates a torque on the pulley. The torque \( \tau \) due to the tension is given by:
\(
\tau = T \cdot R
\)
This torque causes an angular acceleration \( \alpha \) of the pulley. According to the relation between torque and angular acceleration:
\(
\tau = I \cdot \alpha
\)
where \( I \) is the moment of inertia of the pulley. For a solid disk, the moment of inertia is:
\(
I = \frac{1}{2} M R^2
\)
Step 4: Relate linear and angular acceleration
Since the string does not slip over the pulley, we have the relationship between linear acceleration \( a \) and angular acceleration \( \alpha \):
\(
a = \alpha R \tag{2}
\)
Step 5: Substitute the angular acceleration
From equation (2), we can express \( \alpha \) in terms of \( a \):
\(
\alpha = \frac{a}{R}
\)
Substituting this into the torque equation gives:
\(
T \cdot R = \left(\frac{1}{2} M R^2\right) \cdot \left(\frac{a}{R}\right)
\)
Simplifying this, we get:
\(
T \cdot R = \frac{1}{2} M R a
\)
Dividing both sides by \( R \):
\(
T = \frac{1}{2} M a \tag{3}
\)
Step 6: Substitute equation (3) into equation (1)
Now we can substitute the expression for \( T \) from equation (3) back into equation (1):
\(
mg - \frac{1}{2} M a = ma
\)
Rearranging this gives:
\(
mg = ma + \frac{1}{2} M a
\)
Factoring out \( a \) on the right side:
\(
mg = a \left(m + \frac{1}{2} M\right)
\)
Step 7: Solve for acceleration \( a \)
Now we can solve for \( a \):
\(
a = \frac{mg}{m + \frac{1}{2} M}
\)
Final Result
Thus, the acceleration of the block when released is:
\(
a = \frac{2mg}{2m + M}
\)
When the block of mass m is released, the forces acting on it are:
- The gravitational force downward: \( F_g = mg \)
- The tension in the string acting upward: \( T \)
Using Newton's second law for the block, we can write:
\(
mg - T = ma \tag{1}
\)
where \( a \) is the acceleration of the block downward.
The pulley has a mass \( M \) and radius \( R \). The tension in the string creates a torque on the pulley. The torque \( \tau \) due to the tension is given by:
\(
\tau = T \cdot R
\)
This torque causes an angular acceleration \( \alpha \) of the pulley. According to the relation between torque and angular acceleration:
\(
\tau = I \cdot \alpha
\)
where \( I \) is the moment of inertia of the pulley. For a solid disk, the moment of inertia is:
\(
I = \frac{1}{2} M R^2
\)
Since the string does not slip over the pulley, we have the relationship between linear acceleration \( a \) and angular acceleration \( \alpha \):
\(
a = \alpha R \tag{2}
\)
From equation (2), we can express \( \alpha \) in terms of \( a \):
\(
\alpha = \frac{a}{R}
\)
Substituting this into the torque equation gives:
\(
T \cdot R = \left(\frac{1}{2} M R^2\right) \cdot \left(\frac{a}{R}\right)
\)
Simplifying this, we get:
\(
T \cdot R = \frac{1}{2} M R a
\)
Dividing both sides by \( R \):
\(
T = \frac{1}{2} M a \tag{3}
\)
Now we can substitute the expression for \( T \) from equation (3) back into equation (1):
\(
mg - \frac{1}{2} M a = ma
\)
Rearranging this gives:
\(
mg = ma + \frac{1}{2} M a
\)
Factoring out \( a \) on the right side:
\(
mg = a \left(m + \frac{1}{2} M\right)
\)
Now we can solve for \( a \):
\(
a = \frac{mg}{m + \frac{1}{2} M}
\)
Thus, the acceleration of the block when released is:
\(
a = \frac{2mg}{2m + M}
\)
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Solved Examples
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.1
6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
A block of mass m hangs by means of a string which goes over a pulley of mass m and moment of inertia l, as shown in the diagram. The string does not realtive to the pulley. Find the frequency of small oscillations.
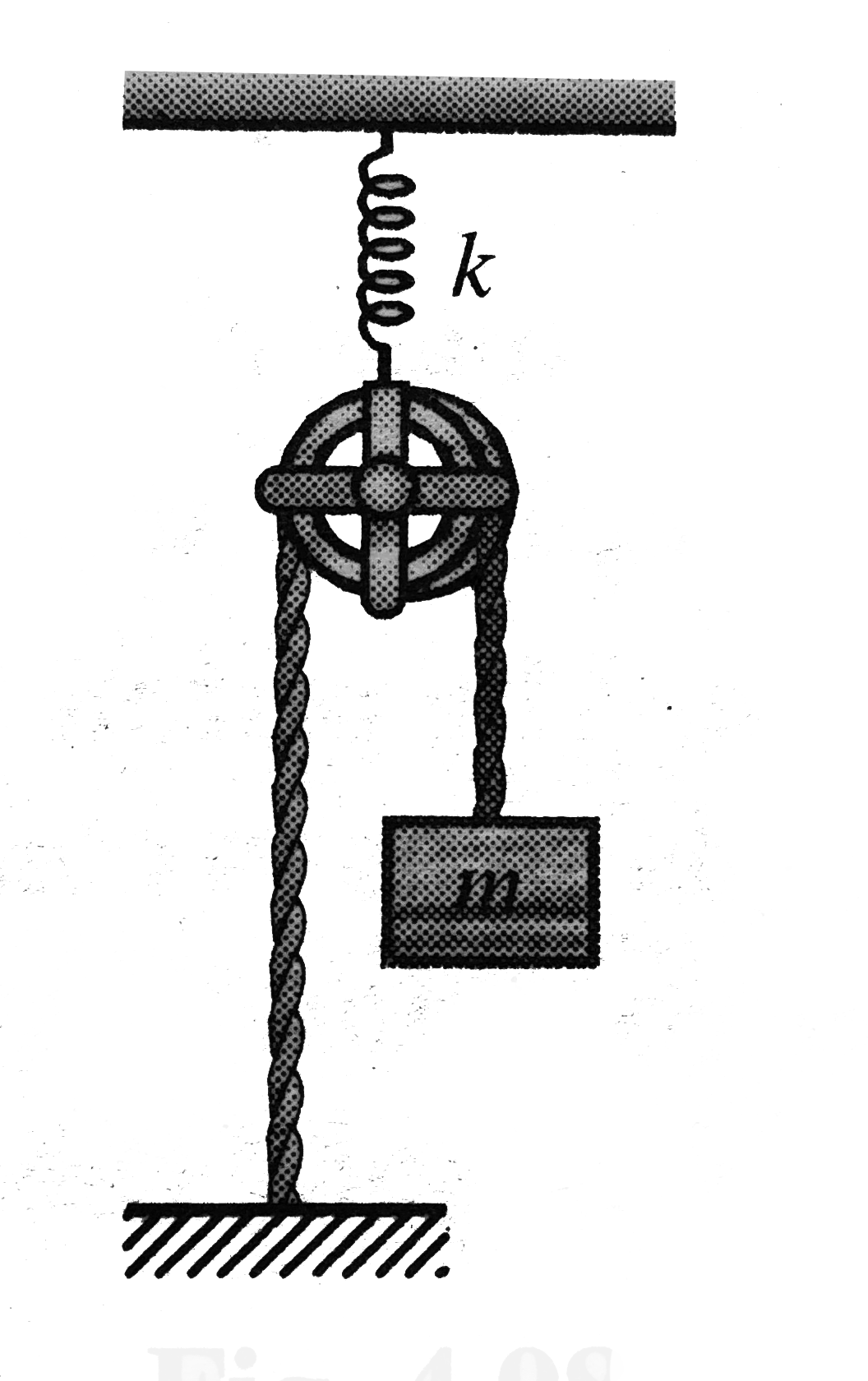
View Solutiontwo masses 2m and m are attached to the the ends of a string while passing over a smooth Pulley of mass m and radius R. The ratio of tensions in both the strings is
_PHY_E05_245_Q01.png)
View SolutionA uniform disc of radius R and mass M is free to rotate about a fixed horizontal axis perpendicular to its plane and passing through its centre. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The block is released from rest. If string does not slip on the rim then find the acceleration of the block. Neglect the mass of the string.
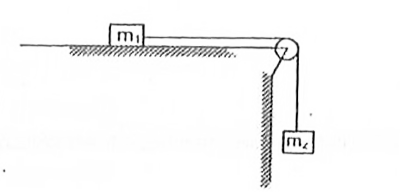
View SolutionA block of mass m1=2 kg is kept on a smooth horizontal table. Another block of mass m2=1 kg is connected to m1 by a light inextensible string passing over a smooth pulley as shown in the figure. If the blocks are released, what will be the (a) acceleration of each block (b) tension in the string?
View SolutionTwo masses M and M/ 2 are joint together by means of a light inextensible string passes over a frictionless pulley as shown in figure. When bigger mass is released the small one will ascend with an acceleration of
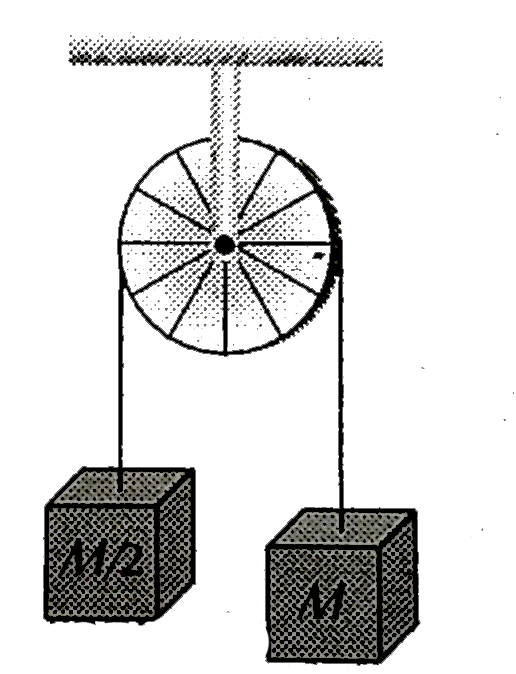
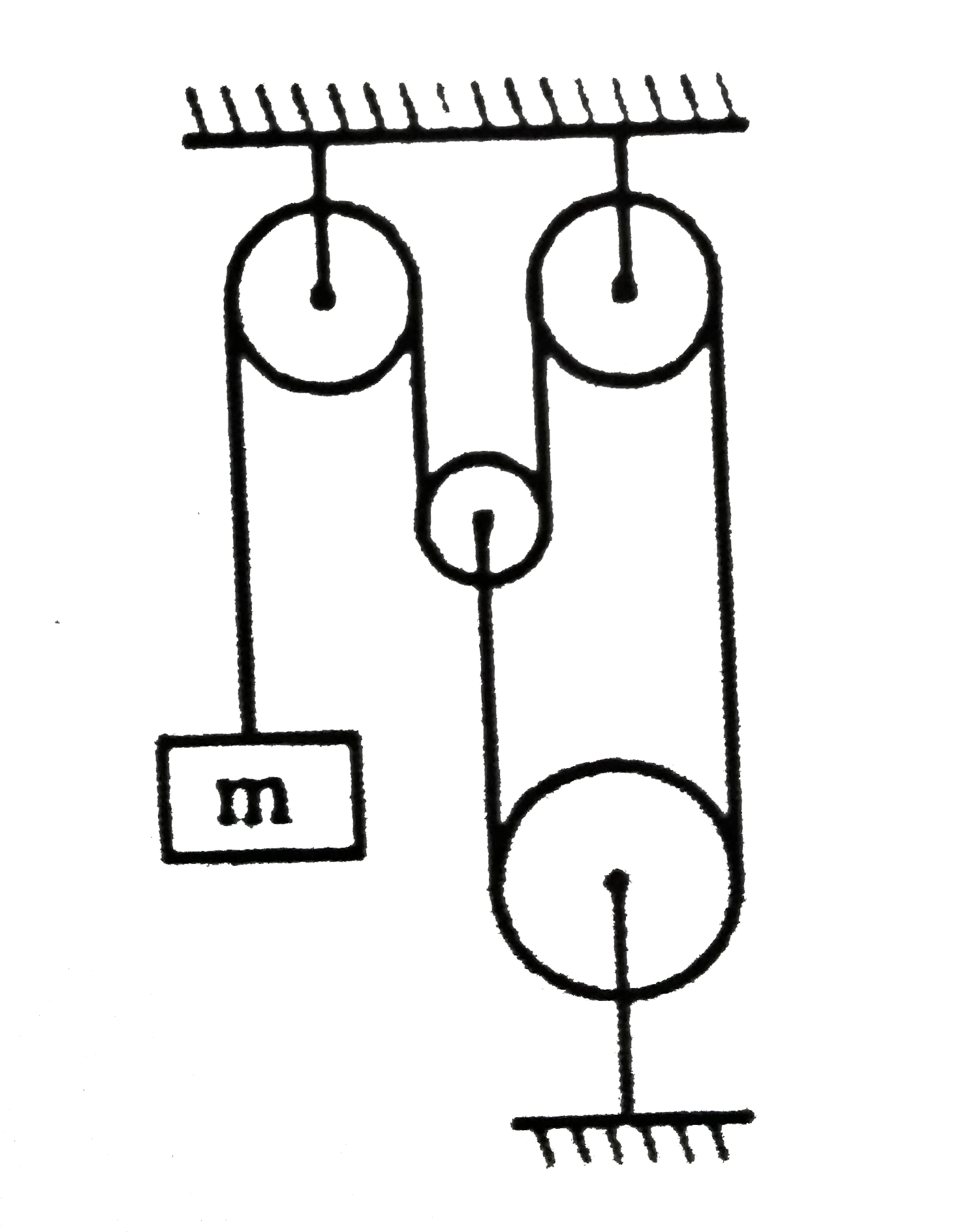
View SolutionIf the string & all the pulleys are ideal, acceleration of mass m is :-
View SolutionTwo masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.
View SolutionTwo unequal masses of 1 kg and 2 kg are attached at the two ends of a light inextensible string passing over a smooth pulley as shown in figure. If the system is released from rest, find the work done by string on both the blocks in 1 s. (Take g = 10 ms−2)

View Solution
In the shown mass pulley system, pulleys and string are massless. The one end of the string is pulleed by the force F=2mg. The acceleration of the block will be
View Solution
In the shown mass pulley system, pulleys and string are massless. The one end of the string is pulleed by the force F=2mg. The acceleration of the block will be
View Solution
