Two masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.
To solve the problem of two masses connected by a string over a frictionless pulley, we will follow these steps:
Step 1: Identify the masses and forces
We have two masses:
- Mass m1=2kg
- Mass m2=4kg
The gravitational force acting on each mass can be calculated using the formula F=m⋅g, where g≈9.8m/s2.
- For m1:
F1=m1⋅g=2⋅9.8=19.6N
- For m2:
F2=m2⋅g=4⋅9.8=39.2N
Step 2: Set up the equations of motion
When the masses are released, m2 (the heavier mass) will accelerate downward, and m1 will accelerate upward. We will denote the acceleration of the system as a and the tension in the string as T.
For mass m1 (2 kg):
T−F1=m1⋅a(1)
Substituting F1:
T−19.6=2a(1)
For mass m2 (4 kg):
F2−T=m2⋅a(2)
Substituting F2:
39.2−T=4a(2)
Step 3: Solve the equations simultaneously
We can solve equations (1) and (2) simultaneously. From equation (1), we can express T:
T=19.6+2a(3)
Substituting equation (3) into equation (2):
39.2−(19.6+2a)=4a
Simplifying this:
39.2−19.6−2a=4a
19.6=6a
a=19.66≈3.27m/s2
Step 4: Find the tension in the string
Now that we have the acceleration, we can substitute a back into equation (3) to find T:
T=19.6+2(19.66)
Calculating:
T=19.6+39.26=19.6+6.53≈26.13N
Final Results
- The acceleration of the masses is approximately 3.27m/s2.
- The tension in the string is approximately 26.13N.
We have two masses:
- Mass m1=2kg
- Mass m2=4kg
F1=m1⋅g=2⋅9.8=19.6N
- For m2:
F2=m2⋅g=4⋅9.8=39.2N
When the masses are released, m2 (the heavier mass) will accelerate downward, and m1 will accelerate upward. We will denote the acceleration of the system as a and the tension in the string as T.
T−F1=m1⋅a(1)
Substituting F1:
T−19.6=2a(1)
F2−T=m2⋅a(2)
Substituting F2:
39.2−T=4a(2)
We can solve equations (1) and (2) simultaneously. From equation (1), we can express T:
T=19.6+2a(3)
39.2−(19.6+2a)=4a
Simplifying this:
39.2−19.6−2a=4a
19.6=6a
a=19.66≈3.27m/s2
Now that we have the acceleration, we can substitute a back into equation (3) to find T:
T=19.6+2(19.66)
Calculating:
T=19.6+39.26=19.6+6.53≈26.13N
- The acceleration of the masses is approximately 3.27m/s2.
- The tension in the string is approximately 26.13N.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE69videos
LAWS OF MOTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-A)65videos
LAWS OF MOTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -J ) Aakash Challengers Questions12videos
LAWS OF MOTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions10videos
KINETIC THEORY
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)26videos
MAGNETISM AND MATTER
Similar Questions
Two masses 2 kg and 4 kg are connected at two ends of light inextensible string passing over a frictionless pulley . If the masses are released , then find the accelaration of the masses and the tension in the string .
View SolutionTwo masses of 3 kg and 4 kg are connected at the two ends of a light inextensible string that passes over a frictionless pulley. Find the acceleration of the masses and the tension in the string, when the masses are released.
View Solution
Knowledge Check
- Question 1 - Select One
Two masses 8 kg and 12 kg are connected at the two ends of a light in extensible string that passes over a friction less pulley Find the acceleration of the masses and tension in the string , when the masses are released
 . Ag4Bg5Cg8Dg6
. Ag4Bg5Cg8Dg6 - Question 2 - Select One
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
Two masses 8 kg and 12 kg are connected at the two ends of a light in extensible string that passes over a friction less pulley. Find the acceleration of the masses and tension in the string , when the masses are released
 . View Solution
. View SolutionTwo bodies of masses 1 kg and 2 kg are connected by a very light string passed over a clamped light smooth pulley. If the system is released from rest, find the acceleration of the two masses and the tension in the string
View SolutionTwo masses M1=5kg, M2=10kg are connected at the ends of an inextensible string passing over a frictionless pulley as shown. When masses are released, then acceleration of masses will be
(a) g (b) g2 (c) g3 (d) g4
 View Solution
View SolutionTwo masses 5 kg and 3 kg are suspended from the ends of an unstretchable light string passing over a frictionless pulley. When the masses are released, the thrust on the pulley is (g = 10ms−2)
View SolutionTwo blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
View SolutionTwo unequal masses of 1 kg and 2 kg are attached at the two ends of a light inextensible string passing over a smooth pulley as shown . If the system is released from rest, find the work done by string on both the blocks in 1 s.
(Take g=10m/s2).
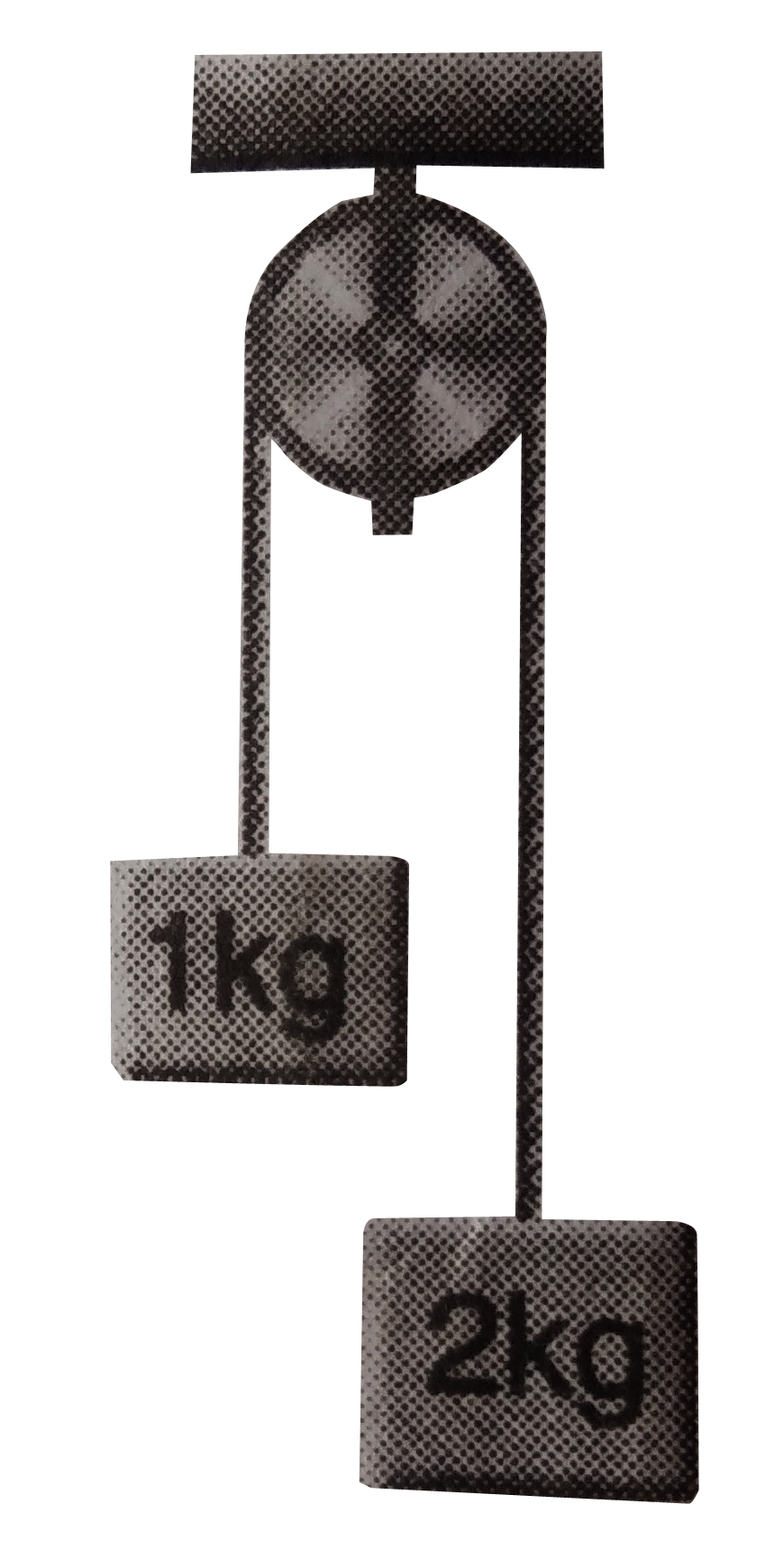 View Solution
View Solution

