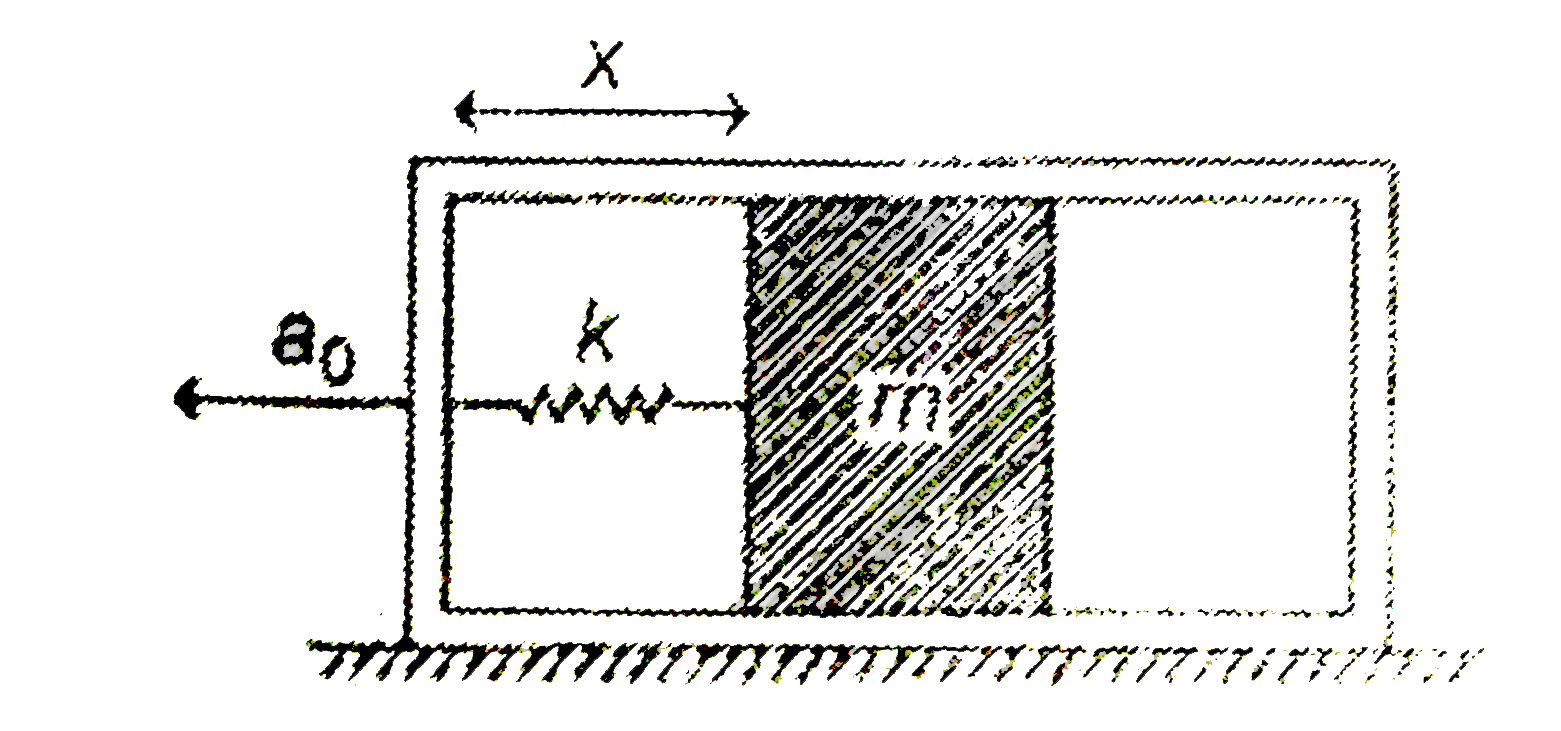
A block of mass m is attached to a frame by a light spring of force constant k. The frame and block are initially at rest with x=x0, the natural length of the spring. If the frame is given a constant horizontal accelration a0 towards left, determine the maximum velocity of the block relative to the frame (block is free to move inside frame). Ignore any friction.
a0√m2k
a0√2mk
a0√mk
12a0√mk
The correct Answer is:C
Step by step video & image solution for A block of mass m is attached to a frame by a light spring of force constant k. The frame and block are initially at rest with x = x_(0), the natural length of the spring. If the frame is given a constant horizontal accelration a_(0) towards left, determine the maximum velocity of the block relative to the frame (block is free to move inside frame). Ignore any friction. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - B More than One Option is Correct
26 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - C Comprehension Type Questions
18 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
A block is suspended by an ideal spring of force constant force F and if maximum displacement of block from its initial mean position of rest is x0 then
View SolutionA block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

View SolutionA block of mass m is connected to a spring of spring constant k as shown in figure. The frame in which the block is placed is given an acceleration a towards left. Neglect friction between the block and the frame walls. The maximum velocity of the block relative to the frame is

View SolutionA block of mass m is kept on a rough horizontal surface and is attached with a massless spring of force constant k. The minimum constant force applied on the other end of the spring of lift the block is
View SolutionA block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is

View SolutionA block of mass m is connected to another block of mass M by a massless spring of spring constant k. the blocks are kept of a smooth horizontal plane and are at rest. The spring is unstretched when a constant force F starts acting on the block of mass M of pull it. Find the maximum extension of the spring

View SolutionA block of mass m attached with a an ideal spring of force constant k is placed on a rough inclined plane having inclination θ with the horizontal and coefficient of friction μ=1/2tanθ, Initially the block is held stationary with the spring in its relaxed state, find the maximum extension in the spring if the block is released.

View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View SolutionA block of mass m=2kg is connected to a a spring of force constant k=50N/m. Initially the block is at rest and tlhe spring has natural length. A constant force F=60N is applied horizontally towards, the maximum speed of the block (in m/s) will be (negelect friction).

View SolutionA block of mass m is connected to a spring of force constant k. Initially the block is at rest and the spring has natural length. A constant force F is applied hrizontally towards right. The maximum speed of the block will be (there is no friction between block and the surface)

View Solution
