A block is suspended by an ideal spring of force constant force F and if maximum displacement of block from its initial mean position of rest is x0 then
increase in energy stored in spring is kx20
x0=3F2k
x0=2Fk
work done by applied force F is Fx0
The correct Answer is:C, D
To solve the problem, we need to analyze the situation of a block suspended by an ideal spring and derive the maximum displacement x0 from its mean position.
1. Understanding the Forces:
The block is subjected to two forces: the gravitational force mg acting downward and the spring force kx acting upward, where k is the spring constant and x is the displacement from the mean position.
2. Equilibrium Condition:
At maximum displacement x0, the block is in equilibrium. Therefore, the downward force due to gravity is balanced by the upward spring force:
mg=kx0
3. Solving for Maximum Displacement:
Rearranging the equation gives:
x0=mgk
4. Work Done by the Applied Force:
The work done W by the applied force F to stretch the spring to the maximum displacement x0 can be calculated using the formula for work done against a spring:
W=F⋅x0
5. Potential Energy in the Spring:
The potential energy stored in the spring at maximum displacement x0 is given by:
PE=12kx20
6. Substituting x0:
Substitute x0=mgk into the potential energy equation:
PE=12k(mgk)2=12m2g2k
7. Final Expressions:
- Maximum displacement: x0=mgk
- Work done by applied force: W=F⋅x0
- Potential energy stored in the spring: PE=12m2g2k
Conclusion:
The maximum displacement x0 of the block from its initial mean position is given by:
x0=mgk
The block is subjected to two forces: the gravitational force mg acting downward and the spring force kx acting upward, where k is the spring constant and x is the displacement from the mean position.
At maximum displacement x0, the block is in equilibrium. Therefore, the downward force due to gravity is balanced by the upward spring force:
mg=kx0
Rearranging the equation gives:
x0=mgk
The work done W by the applied force F to stretch the spring to the maximum displacement x0 can be calculated using the formula for work done against a spring:
W=F⋅x0
The potential energy stored in the spring at maximum displacement x0 is given by:
PE=12kx20
Substitute x0=mgk into the potential energy equation:
PE=12k(mgk)2=12m2g2k
- Maximum displacement: x0=mgk
- Work done by applied force: W=F⋅x0
- Potential energy stored in the spring: PE=12m2g2k
The maximum displacement x0 of the block from its initial mean position is given by:
x0=mgk
Topper's Solved these Questions
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - C Comprehension Type Questions
18 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - D Matrix Matching Type Questions
10 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - A Only One Option is Correct
42 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
A block of mass m is suspended by different springs of force constant shown in figure.

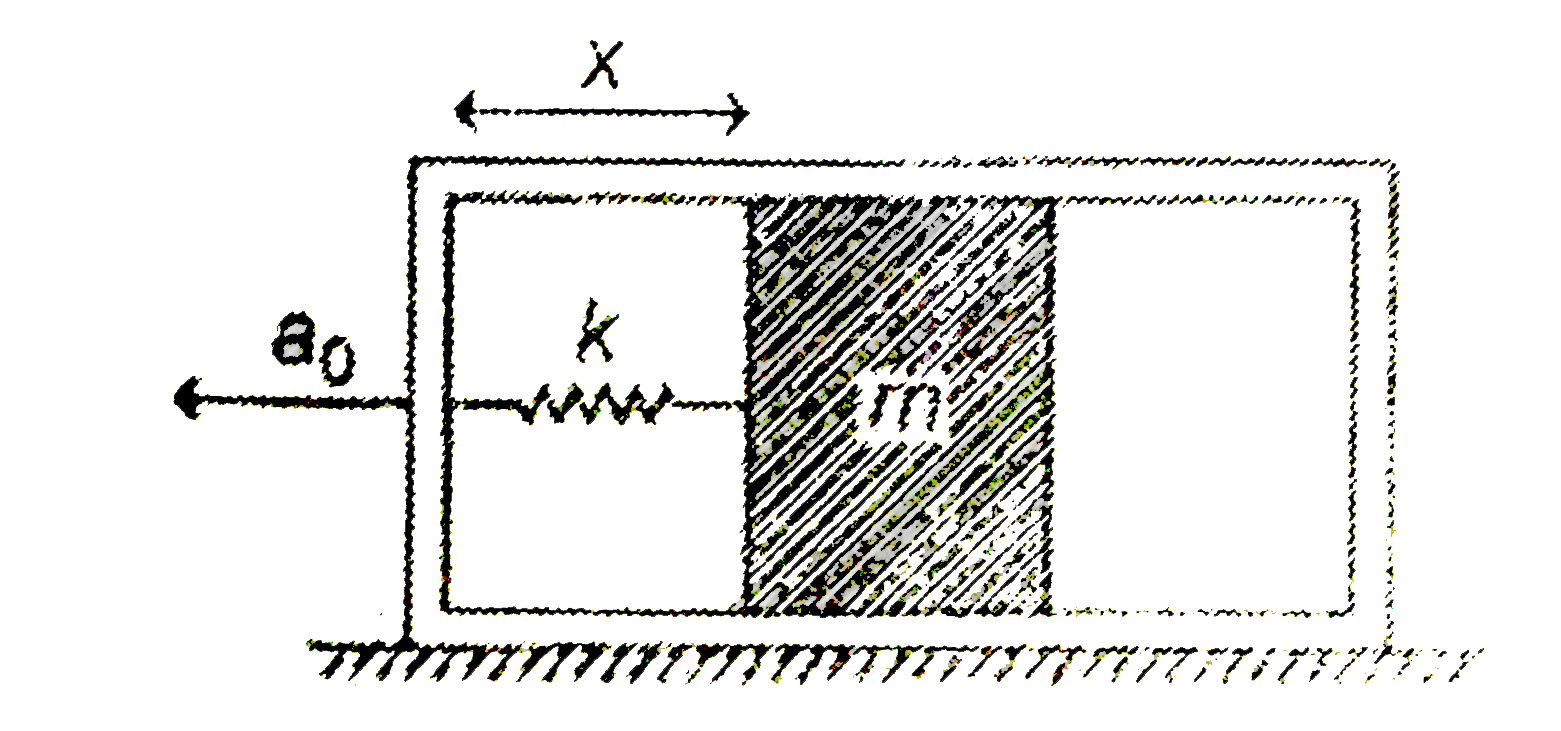
View SolutionA block of mass m is attached to a frame by a light spring of force constant k. The frame and block are initially at rest with x=x0, the natural length of the spring. If the frame is given a constant horizontal accelration a0 towards left, determine the maximum velocity of the block relative to the frame (block is free to move inside frame). Ignore any friction.
View SolutionA block of mass m attached with a an ideal spring of force constant k is placed on a rough inclined plane having inclination θ with the horizontal and coefficient of friction μ=1/2tanθ, Initially the block is held stationary with the spring in its relaxed state, find the maximum extension in the spring if the block is released.

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA block A of mass m connected with a spring of force constant k is executing SHM. The displacement time equation of the block is x=x0+asinωt. An identical block B moving towards negative x -axis with velocity v0 collides elastically with block A at time t=0. Then
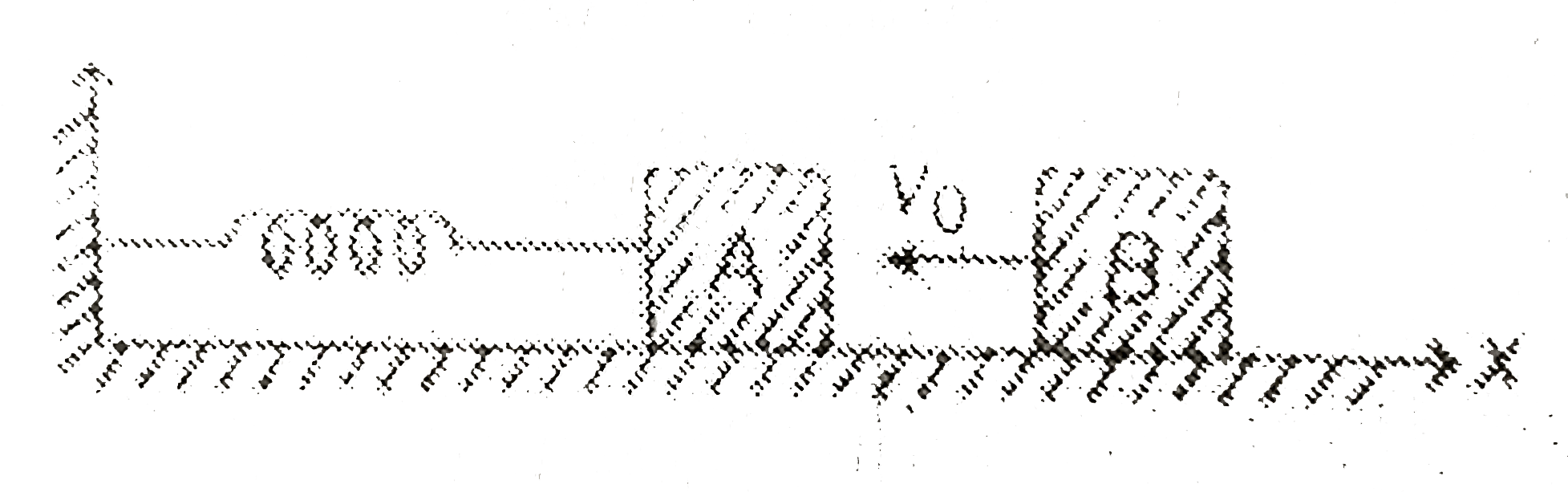
View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.

What is acceleration of centre of mass of system at the instant of maximum elongation of spring
View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.
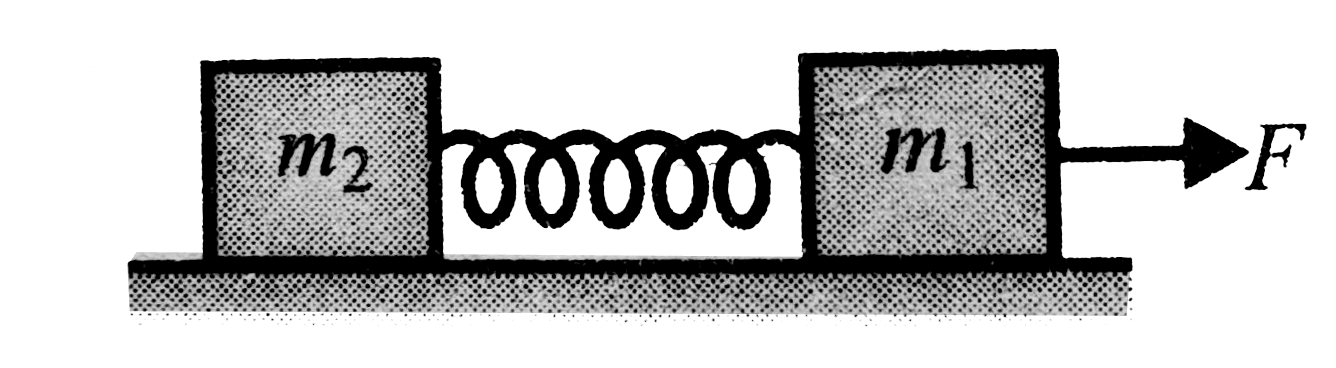
Which of the following statement is not true tn the watt of above system.
View SolutionA block of mass m is suspended through a spring of spring constant k and is in equilibrium. A sharp blow gives the block an initial downward velocity v. How far below the equilibrium position, the block comes to an instantaneous rest?
View SolutionFigure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is

View SolutionA block of mass m=0.1kg is connected to a spring of unknown spring constant k. It is compressed to a distance x from its equilibrium position and released from rest. After approaching half the distance (x2) from the equilibrium position, it hits another block and comes to rest momentarily, while the other block moves with velocity 3ms−1. The total initial energy of the spring is :
View Solution
