A block of mass m is given an initial downward velocity v0 and left on inclined place ( coefficient of friction =0.6). The block will 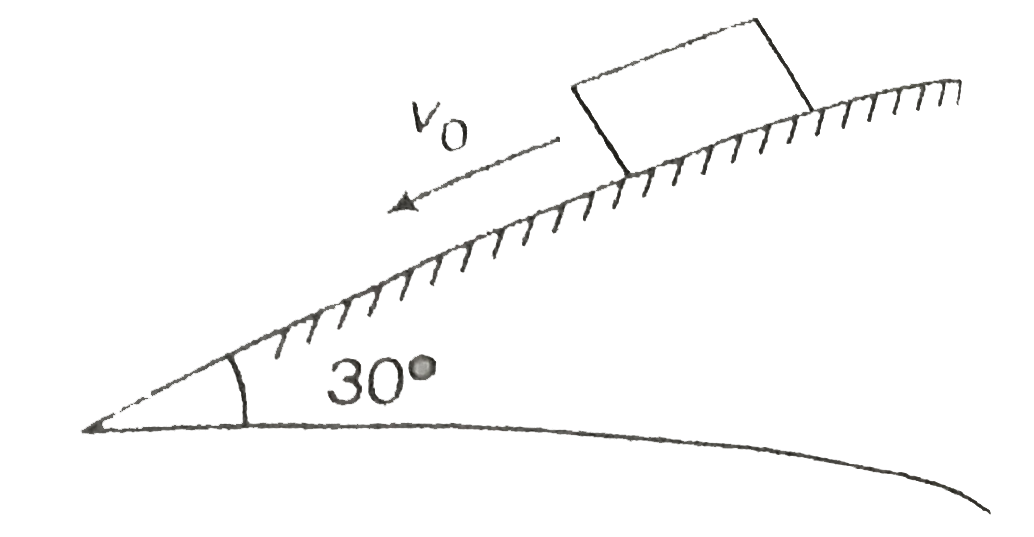
continue of move down the plane with constant velocity v0
accelerate downward
decelerate and come to rest
first accelerate downward then decelerate
The correct Answer is:C
( c) fmax=μmgcosthet=0.6×mg×√32=0.52mg

Since ,fmax>mgsinθ
Block will decelerate and come to rest.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Assertion and reason
28 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Match the columns
7 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.4
20 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
A block of mass 0.5 kg has an initial velocity of 10ms−1 down an inclined plane of angle 30∘, the coefficient of friction between the block and the inclined surface is 0.2. The velocity of the block after it travels a distance of 10 m is

View Solution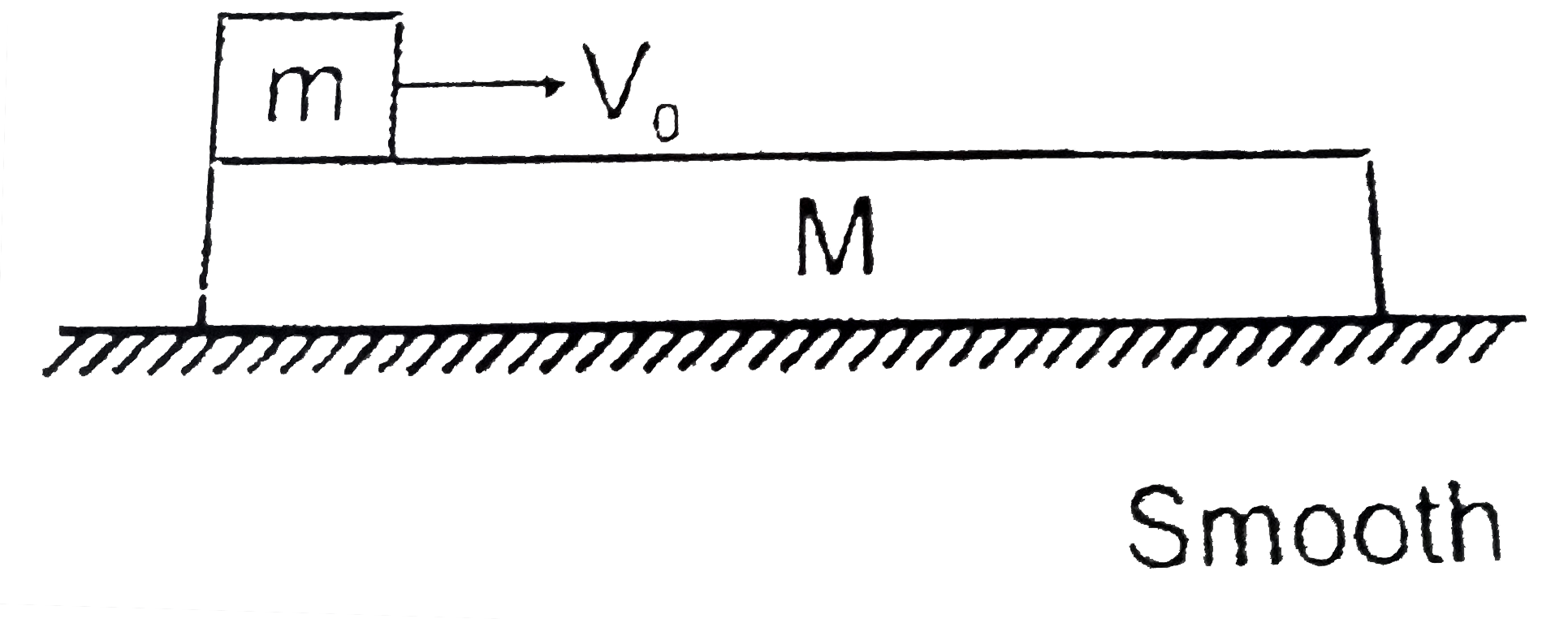
The block of mass m is kept on plank of mass M. The block is given velocity V0 as shown. The coefficient of friction between the block of mass m and plank of mass M is μ and its value is such that block becomes stationary with respect to plank before it reaches the other end. Then:
View Solution
Knowledge Check
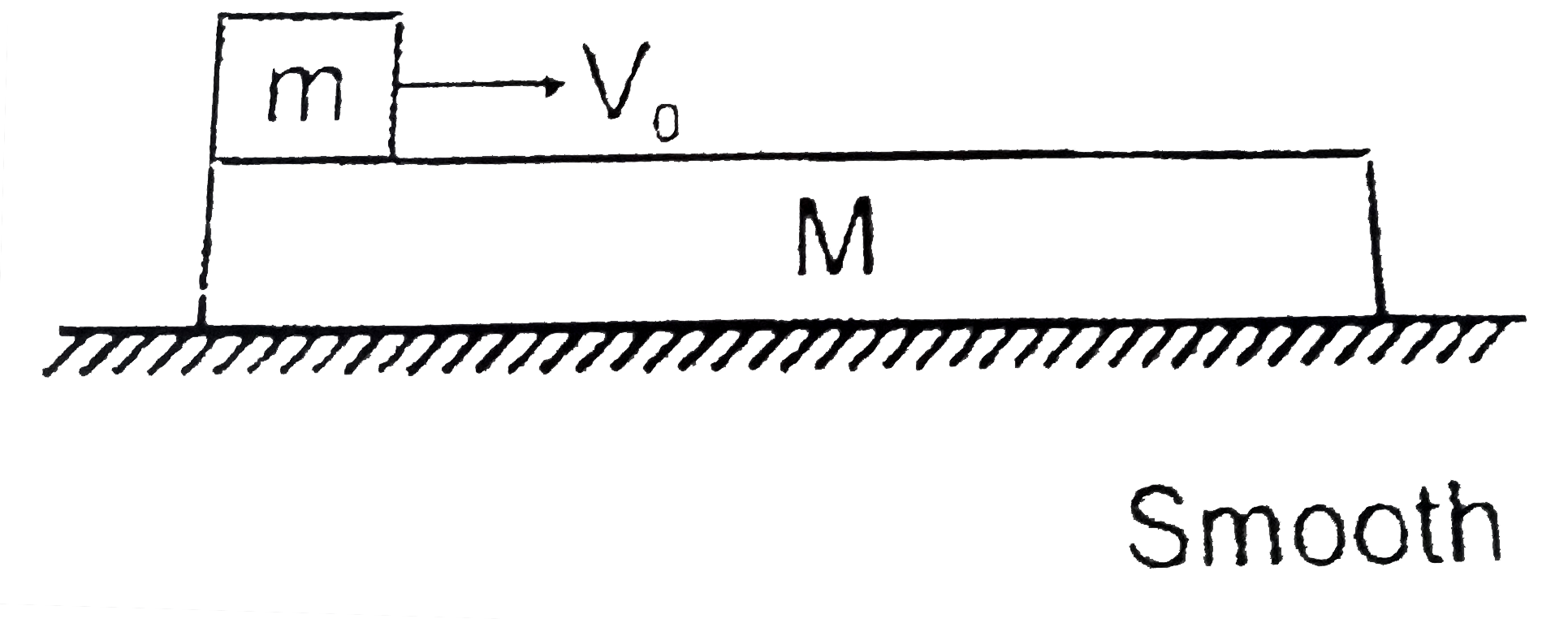
The block of mass m is kept on plank of mass M. The block is given velocity V0 as shown. The coefficient of friction between the block of mass m and plank of mass M is μ and its value is such that block becomes stationary with respect to plank before it reaches the other end. Then:AThe work done b friction on the block is negativeBthe work done by friction on the plank is positiveCthe net work done by friction is negativeDnet work done by the friction is zero.A long block A is at rest on a smooth horizontal surface. A small block B whose mass is half of mass of A is placed on A at one end and is given an initial velocity u as shown in figure. The coefficient of friction between the blocks is μ.
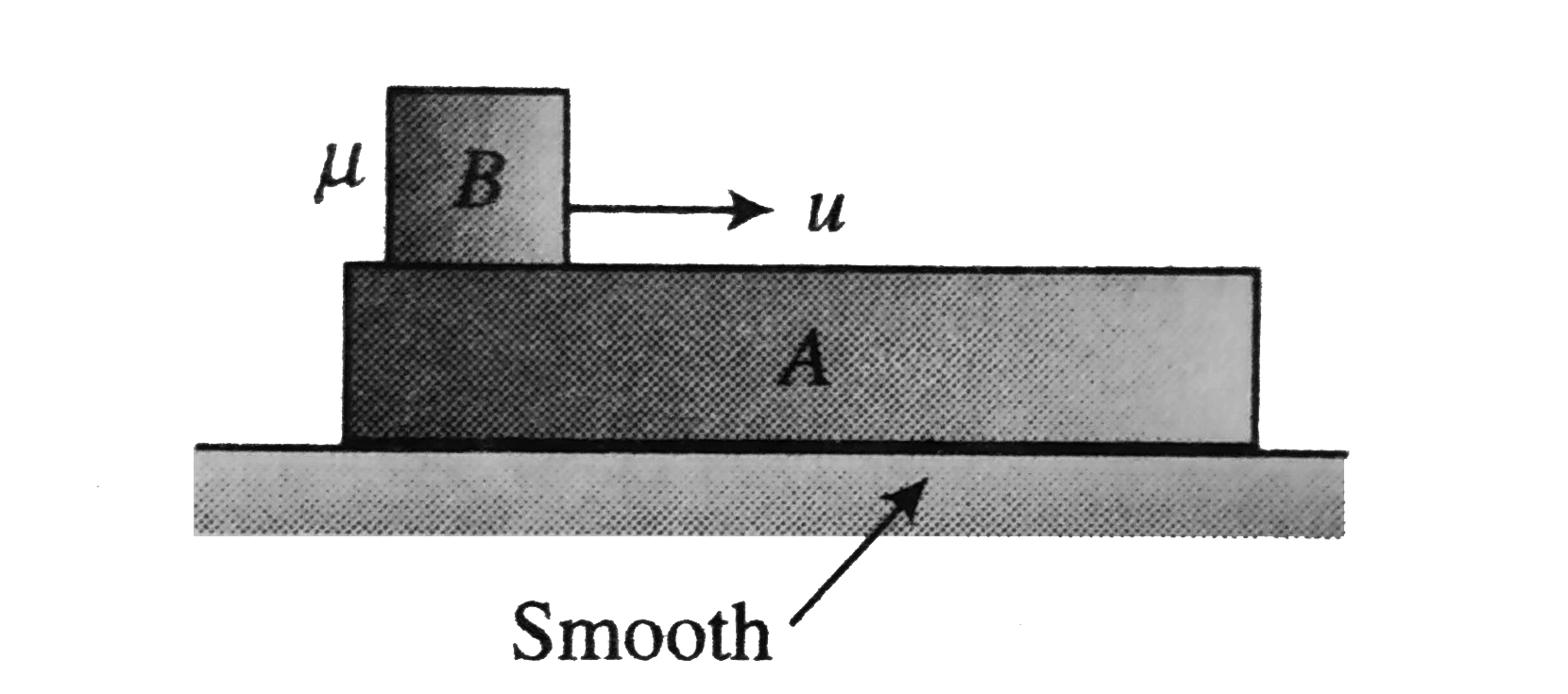 A(a) Finally both move with a common velocity 2u/3.B(b) Acceleration of B relative to A initially is 3μg/2 towards left.C(c) Magnitude of total work done by friction is equal to the final kinetic energy of the system.D(d) The ratio of initial to final momentum of the system is 1.
A(a) Finally both move with a common velocity 2u/3.B(b) Acceleration of B relative to A initially is 3μg/2 towards left.C(c) Magnitude of total work done by friction is equal to the final kinetic energy of the system.D(d) The ratio of initial to final momentum of the system is 1.A block with a square base measuring axa and height h, is placed on an inclined place. The coefficient of friction is m. The angle of inclination (θ) of the plane is gradually increased. The block will.
Atopple before sliding if μ>ahBtopple before sliding if μ<ahCslide before toppling if μ>ahDslide before toppling if μ<ah
A long block A is at rest on a smooth horizontal surface. A small block B whose mass is half of mass of A is placed on A at one end and is given an initial velocity u as shown in figure. The coefficient of friction between the blocks is μ.

View SolutionA block of mass m is projected up with a velocity v0 along an inclined plane of angle of inclination θ=37∘. The coefficient of friction between the inclined plane AB and blocks is μ(=tanθ). Find the values of v0 so that the block moves in a circular path from B to C.
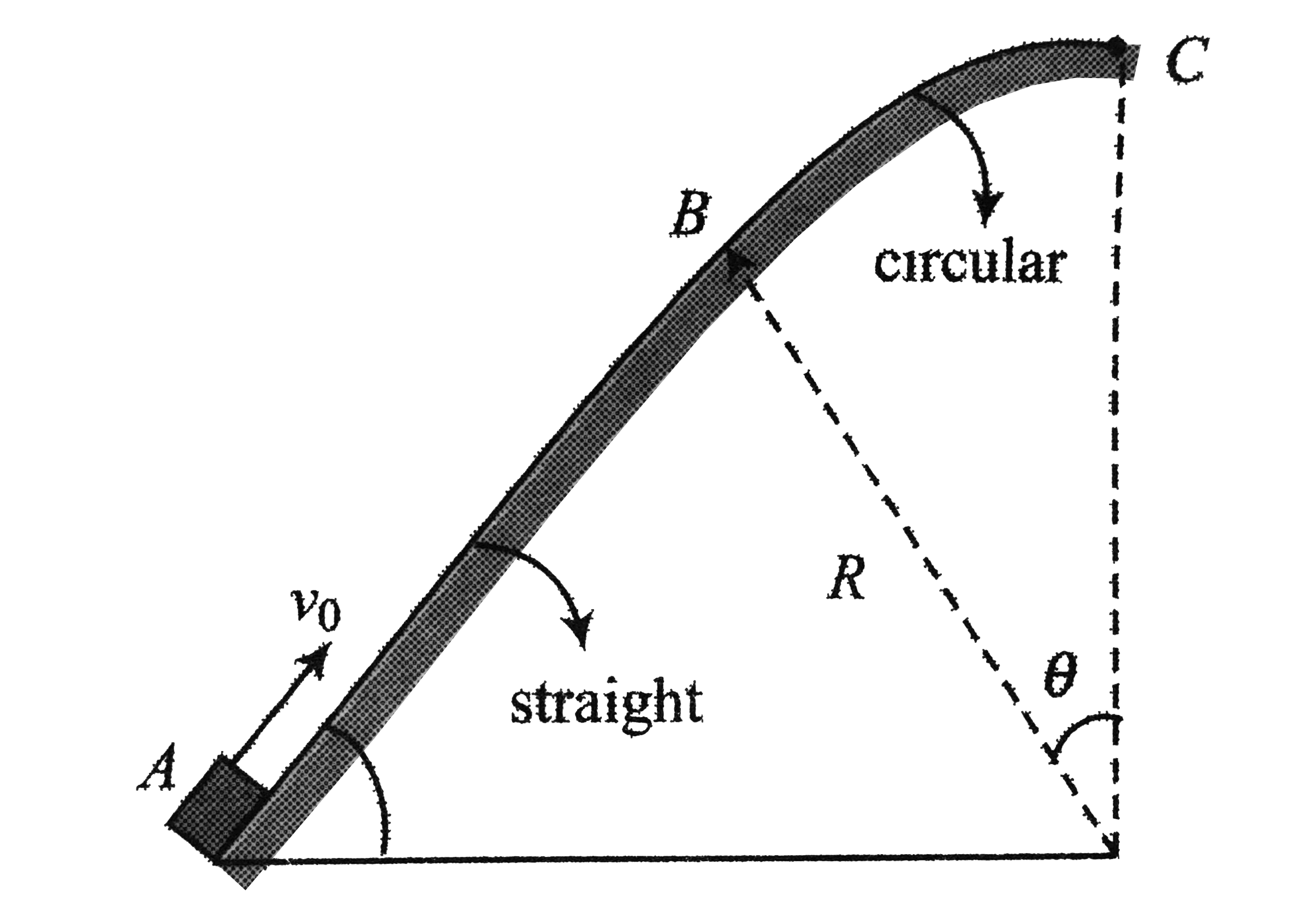
View SolutionA block of mass m is projected up with a velocity v0 along an inclined plane of angle of inclination θ=37∘. The coefficient of friction between the inclined plane AB and blocks is μ(=tanθ). Find the values of v0 so that the block moves in a circular path from B to C.

View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal.If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View Solution
