A block of mass 'm' is hanging from a massless spring of spring constant K. It is in equilibrium under the influence of gravitational force. Another particle of same mass 'm' moving upwards with velocity ao hits the block and sticks to it. For the subsequent motion, choose the incorrect statements:

Velocity of the combined mass must be maximum at natural length of the spring.
Velocity of the combined mass must be maximum at the new equilibrium position.
Velocity of the combined mass must be maximum at the instant particle hits the block.
Velocity of the combined mass must be maximum at a point lying between old equilibrium position and natural length.
The correct Answer is:A, C, D
In a SHM, the mximum velocity is at the equilibrium position.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
Knowledge Check
A particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mkA block of mass m is suspended by different springs of force constant shown in figure.
 AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4
AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4Consider a block of mass 'm' attached to a spring of spring constant 'K' as shown. Now a block of same mass 'm' moving with velocity 'u' strikes the other block and stick to it. Both blocks collectively start performing SHM.
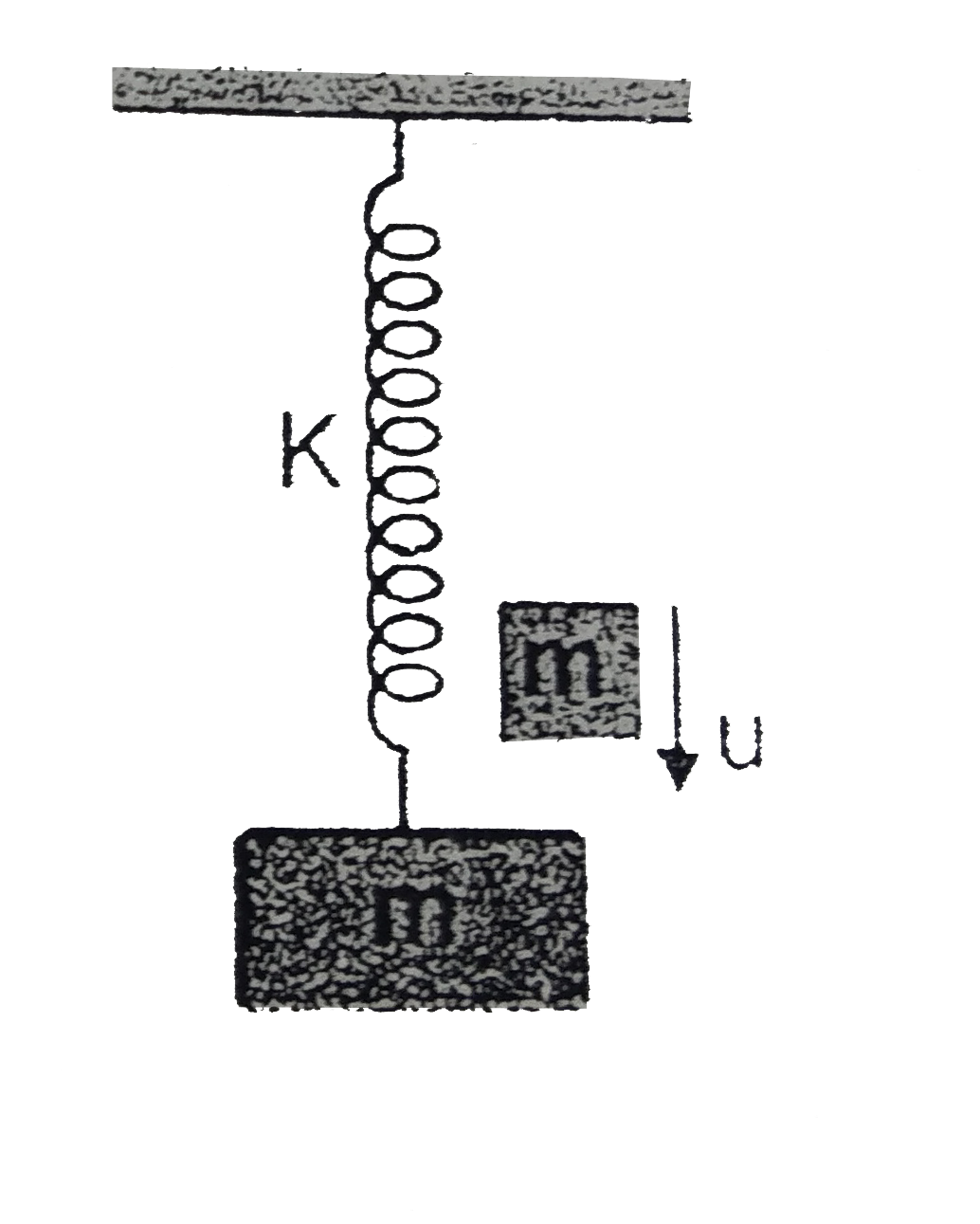
Choose the correct option(s) :AThe maximum extension in the spring is 2mgK+A (Where 'A' is amplitude)BThe maximum extension in the spring is 2mgK (Where 'A' is amplitude)CThe velocity of the block at the instant is at maximum extension is zero.DThe maximum extension in the spring is 2mgK+2A (Where 'A' is amplitude)
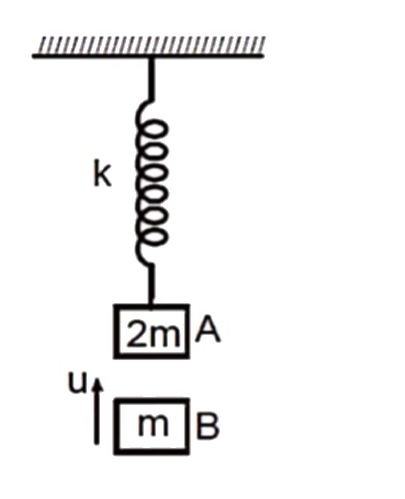
A block A of mass 2m is hanging from a vertical massless spring of spring constant k and is in equilibrium. Another block B of mass m strikes the block A with velocity u and sticks to it as shown in the figure. The magnitude of the acceleration of the combined system of the blocks just after the collision is
View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View SolutionA block of mass m is suspened through a spring of spring constant k and is in equlibrium. A sharp blow gives the block an initial downward velocity v. How far below the equilibrium psitin, the block comes to an instantaneous rest?
View SolutionA block of mass m hangs from three springs having same spring constant k. If the mass is slightly displaced downwards, the time period of oscillation will be

View SolutionConsider a block of mass 'm' attached to a spring of spring constant 'K' as shown. Now a block of same mass 'm' moving with velocity 'u' strikes the other block and stick to it. Both blocks collectively start performing SHM.

The amplitude (A) of their SHM is
View Solution
