Consider a block of mass 'm' attached to a spring of spring constant 'K' as shown. Now a block of same mass 'm' moving with velocity 'u' strikes the other block and stick to it. Both blocks collectively start performing SHM.

The amplitude (A) of their SHM is
mgK
2mgK
√mμ22K+m2g2K2
√mμ22K−m2g2K2
The correct Answer is:C
v=ω√A2−x2
u2=√K2m√A2−(mgK)2
u24=K2m×(A2−m2g2K2)
A=√μ22K+m2g2K2
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - Physics775videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PT-0130videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS SEC - 220videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems13videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - PHYSICS127videos
TEST SERIES
Similar Questions
A block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionFigure shown a block P of mass m resting on a smooth horizontal ground, attached to one and a spring of force constant k in netural length. If another block od same mass and moving with a velocity u towards right is placed on the block on which stick to it due to friction ,find the time it will take to reach its exterme position. Also find the amplitude of oscillation of the combined mass 2m.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
Consider a block of mass 'm' attached to a spring of spring constant 'K' as shown. Now a block of same mass 'm' moving with velocity 'u' strikes the other block and stick to it. Both blocks collectively start performing SHM.
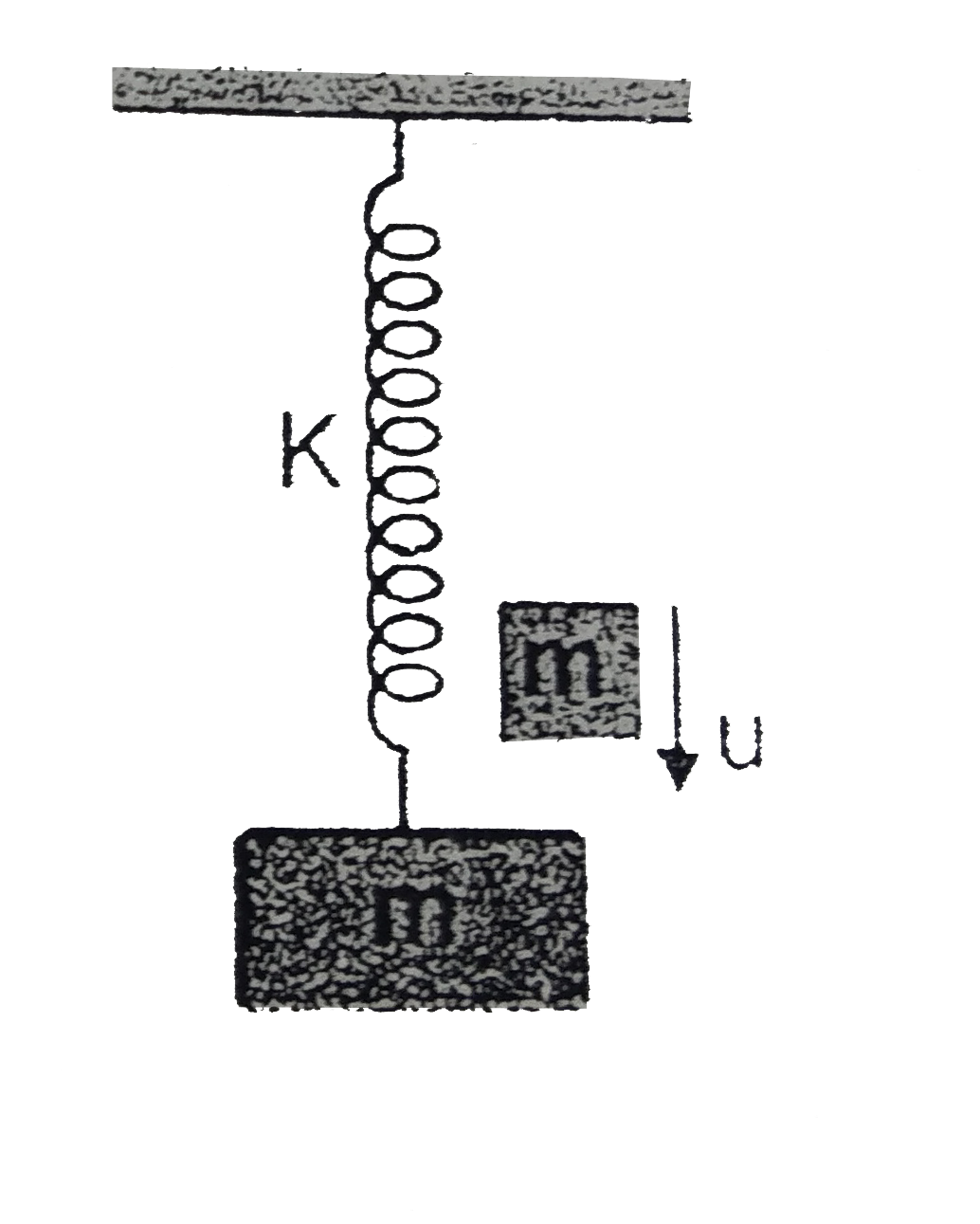
Choose the correct option(s) :AThe maximum extension in the spring is 2mgK+A (Where 'A' is amplitude)BThe maximum extension in the spring is 2mgK (Where 'A' is amplitude)CThe velocity of the block at the instant is at maximum extension is zero.DThe maximum extension in the spring is 2mgK+2A (Where 'A' is amplitude) - Question 2 - Select One
A block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
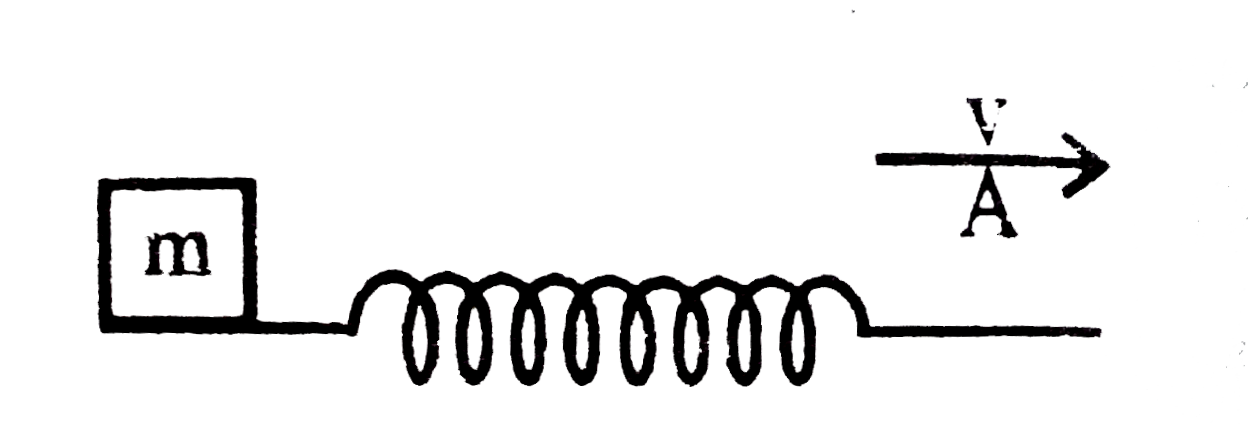 A14√mv2kB√mv2kC12√mv2kD2√mv2k
A14√mv2kB√mv2kC12√mv2kD2√mv2k - Question 3 - Select One
Calculate the period of oscillations of block of mass m attached with a set of springs as shown
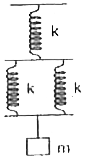 A2π√m3kB2π√3m2kC2π√2m3kD2π√3km
A2π√m3kB2π√3m2kC2π√2m3kD2π√3km
A block of mass m is suspended by different springs of force constant shown in figure.
 View Solution
View Solution
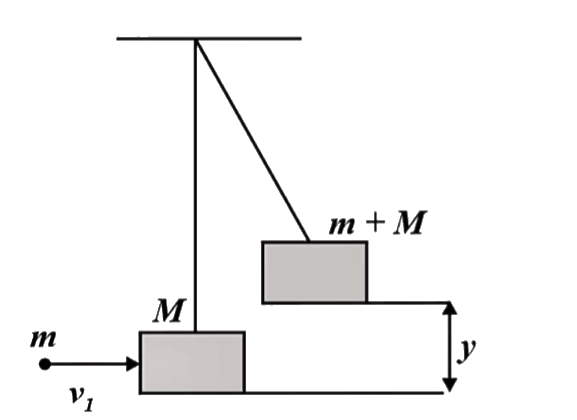
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will beView SolutionA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is
 View Solution
View SolutionA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is
 View Solution
View SolutionA block of mass 'm' is hanging from a massless spring of spring constant K. It is in equilibrium under the influence of gravitational force. Another particle of same mass 'm' moving upwards with velocity ao hits the block and sticks to it. For the subsequent motion, choose the incorrect statements:
 View Solution
View Solution

