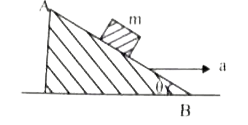
A block of mass m is lying on a wedge having inclination angle α=tan−1(15) wedge is moving with a constant acceleration a=2ms−2 The minimum value of coefficient of friction μ so that m remain stationary w.r.t. wedge is

2/9
5/12
1/5
2/5
The correct Answer is:b
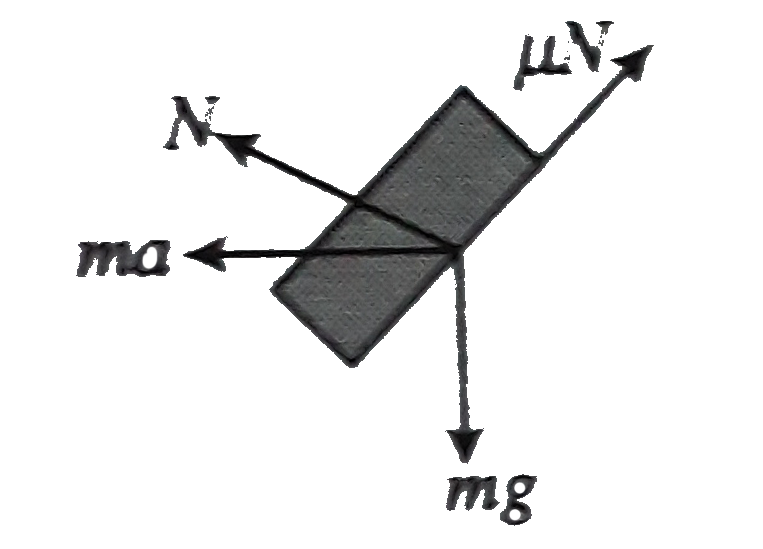
FBD of m in frame of wedge
N=mgcosα−masinα
Now f=μN=macosα+mgsinα
μ=acosα+gsinαgcosα−asinα
=a+gtanαg−tanα=512
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple Correct2videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Linked Comprehension52videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Subjective21videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
Similar Questions
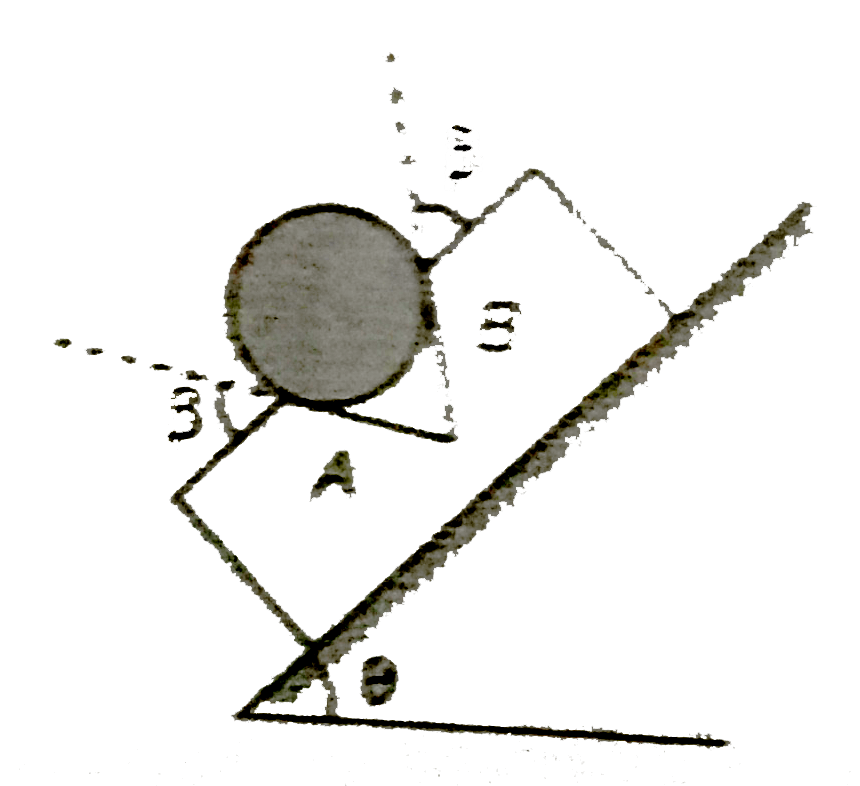
A uniform cylinder of radius r and radius of gyration is kept on a fixed wedge of inclination θ. When we push the wedge with a constant acceleration a, the cylinder rolls up the wedge. Find coefficient of friction between the cylinder and wedge.
 View Solution
View SolutionA block of mass m is placed on the rough incline of a wedge of mass M and inclination α to the horizontal. Calculate the maximum and minimum acceleration that can be imparted to the wedge so that the block may remain stationary relative to the wedge. The coefficient iof friction between the block and the wedge is μ.
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m resting on a wedge of angle θ as shown in the figure. The wedge is given an acceleration a. What is the minimum value of a so that the mass m falls freely ?
 AgBgcosθCgcotθDgtanθ
AgBgcosθCgcotθDgtanθ - Question 2 - Select One
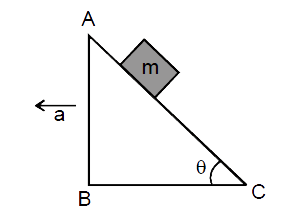
A block of mass m is placed on a smooth inclined wedge ABC of inclination theta as shown in the figure. The wedge is given an acceleration a towards the right. The relation between a and theta for the block to remain stationary on the wedge is.
 Aa=gtanθBa=gcosecθCa=cosθDa=gsinθ
Aa=gtanθBa=gcosecθCa=cosθDa=gsinθ - Question 3 - Select One
The air of density ρ and moving with a velocity v strikes perpendicular the inclined surface of area A and of a wedge kept on a horizontal surface. The mass of the wedge is m. Assuming the collisions to be perfectly inelastic, the minimum value of the coefficient of friction between the wedge and the ground so that the wedge does not move is (Assume mass of particles of air is negligible)
 AρAv2sinθmg+ρAv2cosθBtanθCρAv2mgtanθDρAv2mg+ρAv2cosθ
AρAv2sinθmg+ρAv2cosθBtanθCρAv2mgtanθDρAv2mg+ρAv2cosθ
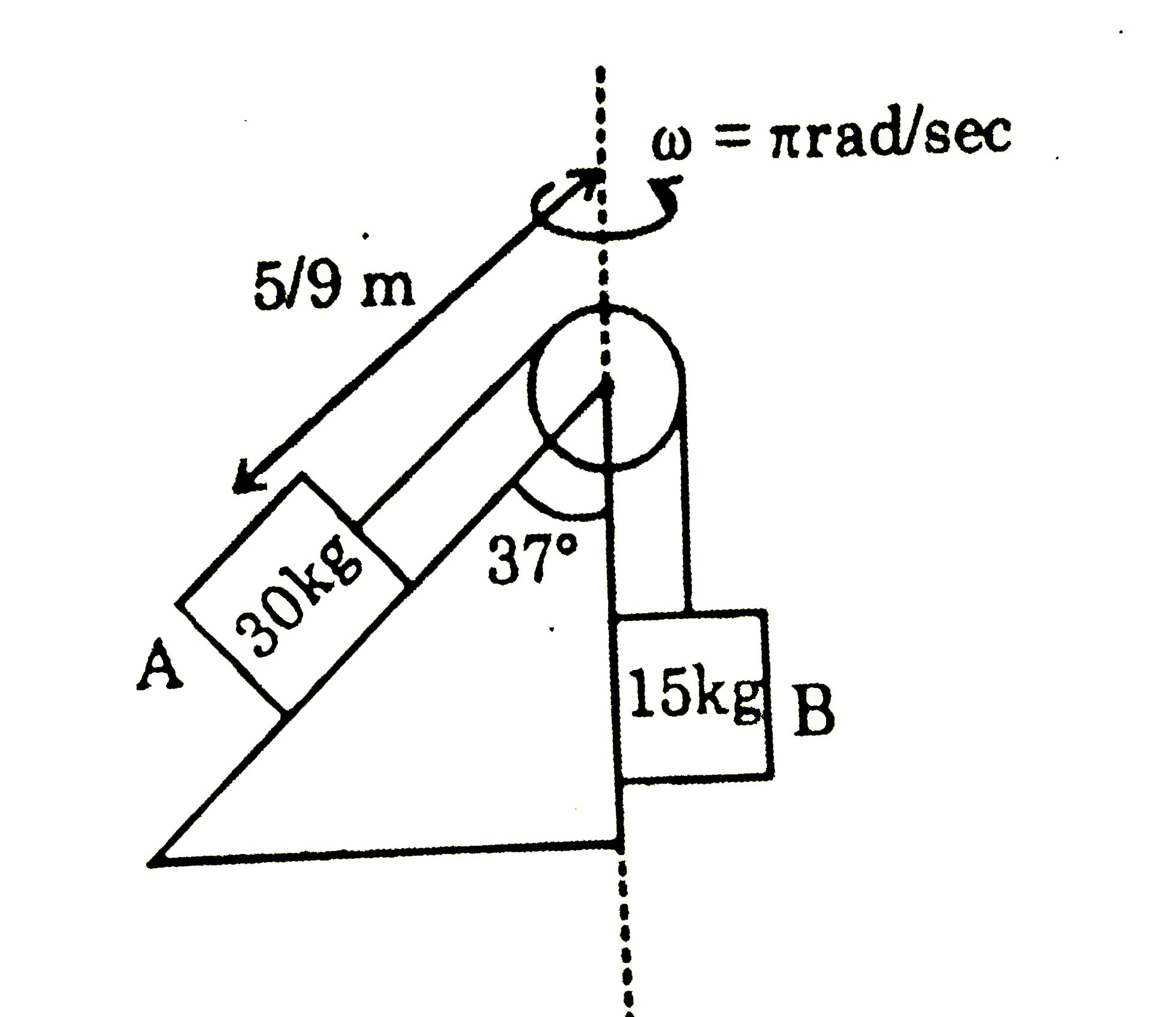
Two small blocks of mass mA=30 kg & mB =15 kg are connected with spring & kept on the wedge which is rotating about given axis as shown in figure. If blocks B remain in rest then minimum value of coefficient of friction between block A & wedge is μ0, then the value of μ20 is :
 View Solution
View SolutionA block of mass 2 kg is kept on a smooth wedge of mass 3 kg and wedge is kept on a rough horizontal surface. A vertical force of 60 N is applied on the minimum coefficient of friction between the wedge and horizontal surface, so that wedge remains at rest during the motion of block on the wedge ?
 View Solution
View SolutionA block of mass m is placed on a smooth inclined wedge ABC of inclination θ as shown in the figure. The wedge is given an acceleration 'a' towards the right. The relation between a and for the block to remain stationary on the wedge is:
 View Solution
View SolutionA block of mass 1kg is at rest relative to a smooth wedge moving leftwards with constant acceleration a=5m/s−2 .Let N be the normal reation between the block and the wedge . Then (g=10m/s−2)
 View Solution
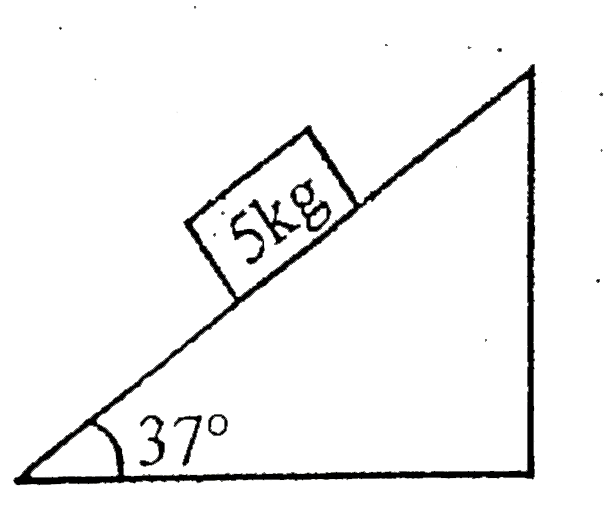
View SolutionA block of mass "5kg" is placed on a wedge having inclination of 37∘ with the horizontal. Coefficient of friction between block and wedge is 0.8. Then select the correct statement.
 View Solution
View Solution

