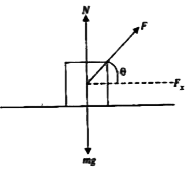
A block of mass m is placed on a horizontal frictionless table. Under the action of a force of constant magnitude the block starts moving. During the translatory motion of the block the angle between the direction of the force varies as where b is a constant, and s is the distance travelled by the block from its initial position. Derive an expression for the velocity of the block in terms of the angel .
If is the force producing a uniform acceleration on a body of mass m, then
But
Integrating
But
.
Topper's Solved these Questions
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - ADDITIONAL SOLVED PROBLEMS
138 Videos
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - CONCEPTUAL SHORT ANSWER QUESTIONS WITH ANSWERS
20 Videos
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
9 Videos
- FRICTIONBOOK - ICSECHAPTER - FRICTIONEXERCISE - Selected problems
30 Videos
Similar Questions
A block of mass m resting on a smooth horizontal plane starts moving due to a constant force F=mg/3 of constant magnitude. In the process of its rectilinear motion the angle θ varies as θ=λs, where λ is constant and s is the distance traversed by the block from its intial position. Find the velocity of the block as a function of the angle θ. Also show that the block will never lose contact with the ground.
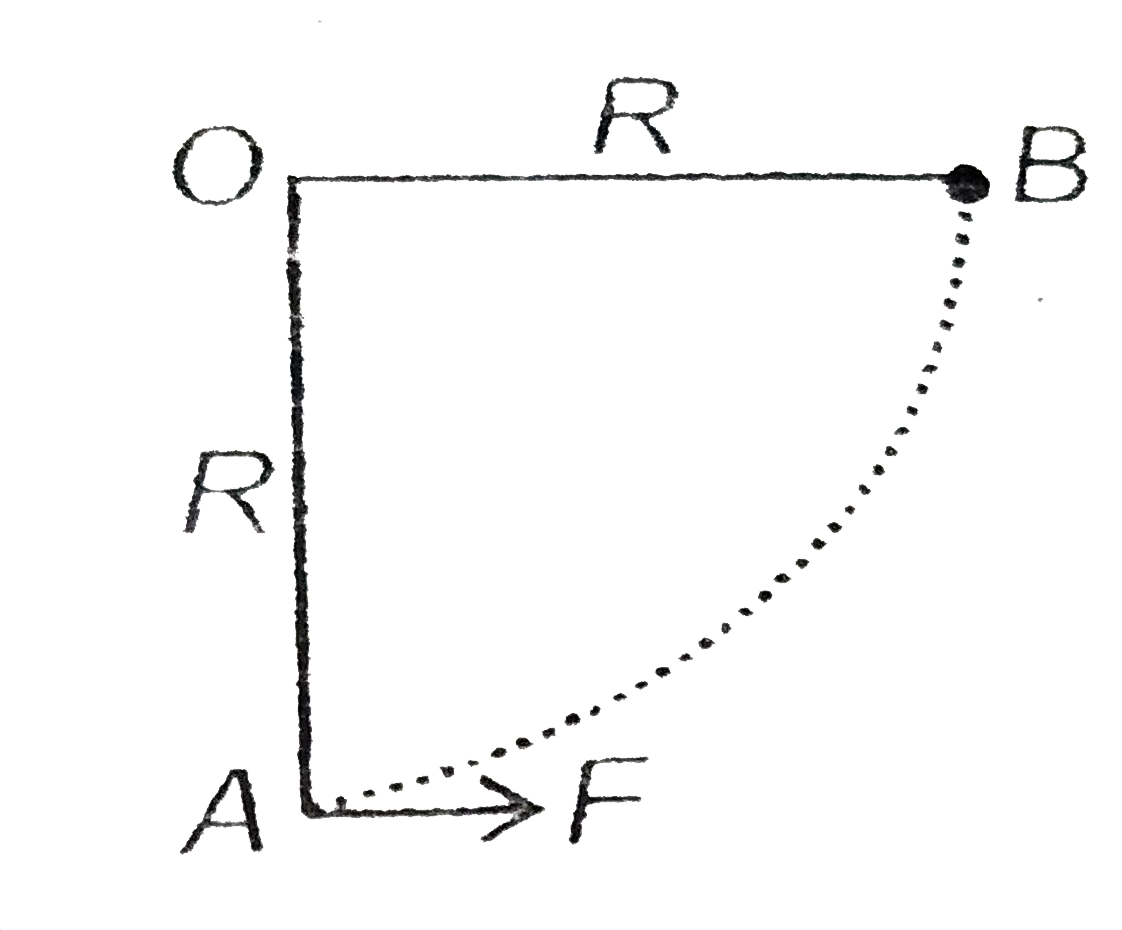
View SolutionA block of mass m is taken from A to B under the action of a constant force F. Work done by this force is
View Solution
Knowledge Check
A block is placed on a horizontal table. Identify the force of action
Aweight of blockBsupport of table on the blockCeither (a) or (b)Dneither (a) nor (b).A block of mass m is placed on a horizontla surface. If the block is pulled by applying a force of magnitude F=5mg at an angle θ=37∘, with horizontal as shown in fig. find the acceleration of the block at the given instant.
 A5√5gB3√5gC2√3gD2√5g
A5√5gB3√5gC2√3gD2√5gA block of mass m is placed on a rough horizontal floor and it is pulled by a ideal string by a constant force F as shown. As the block moves towards right the friction force on block
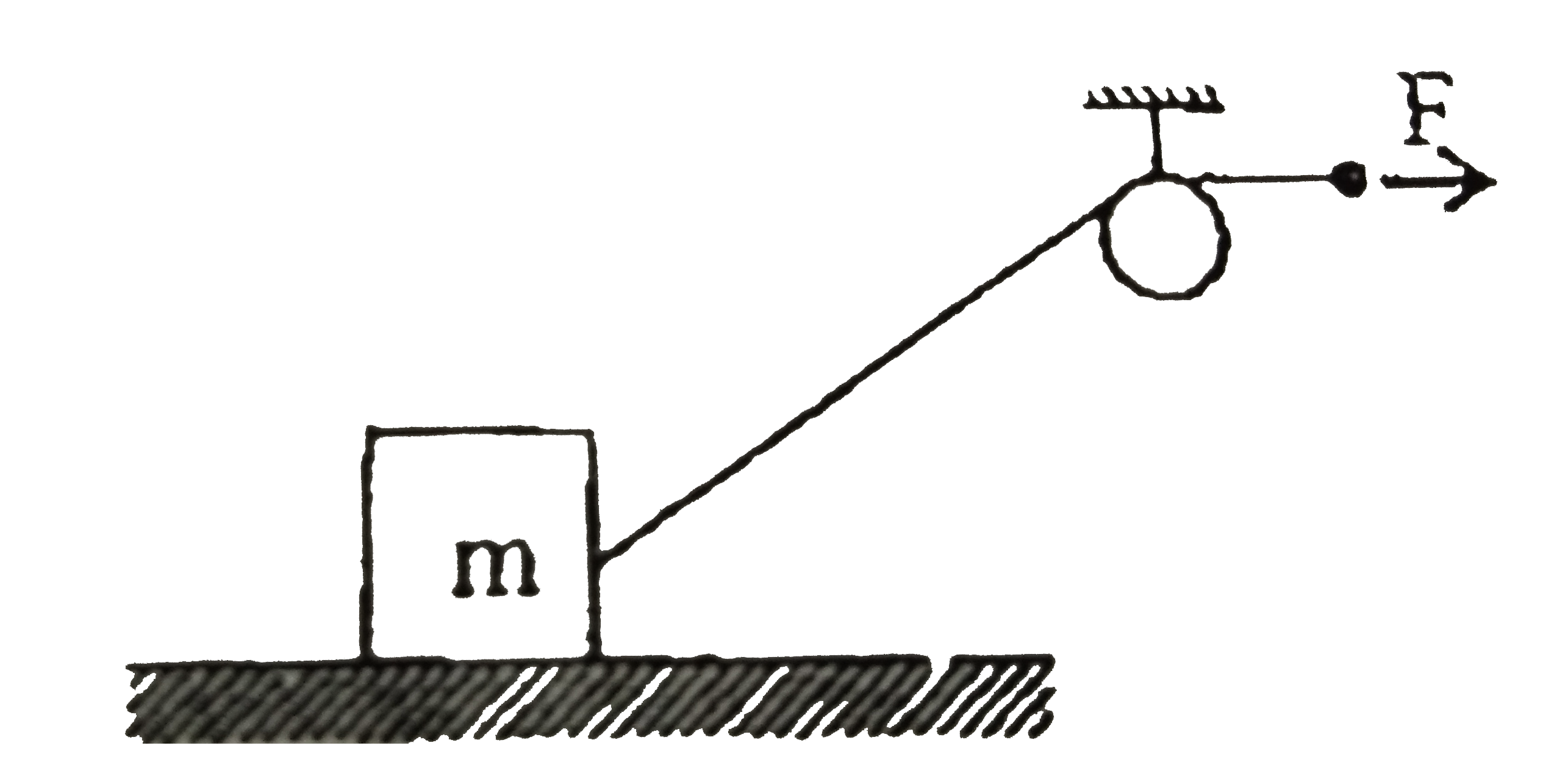 Aremains constantBincreasesCdecreasesDcan not be said
Aremains constantBincreasesCdecreasesDcan not be said
A block of mass m is taken from A to B under the action of a constant force F. Work done by this force is

View SolutionA block of mass m is placed on a horizontla surface. If the block is pulled by applying a force of magnitude F=5mg at an angle θ=37∘, with horizontal as shown in fig. find the acceleration of the block at the given instant.

View SolutionA block of mass m is placed on a rough horizontal floor and it is pulled by a ideal string by a constant force F as shown. As the block moves towards right the friction force on block

View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View Solution
