A block of mass m is placed on a horizontla surface. If the block is pulled by applying a force of magnitude F=5mg at an angle θ=37∘, with horizontal as shown in fig. find the acceleration of the block at the given instant.

Three forces act on the block (a) mg⏐↓(b)F=5mg(c)N↑⏐
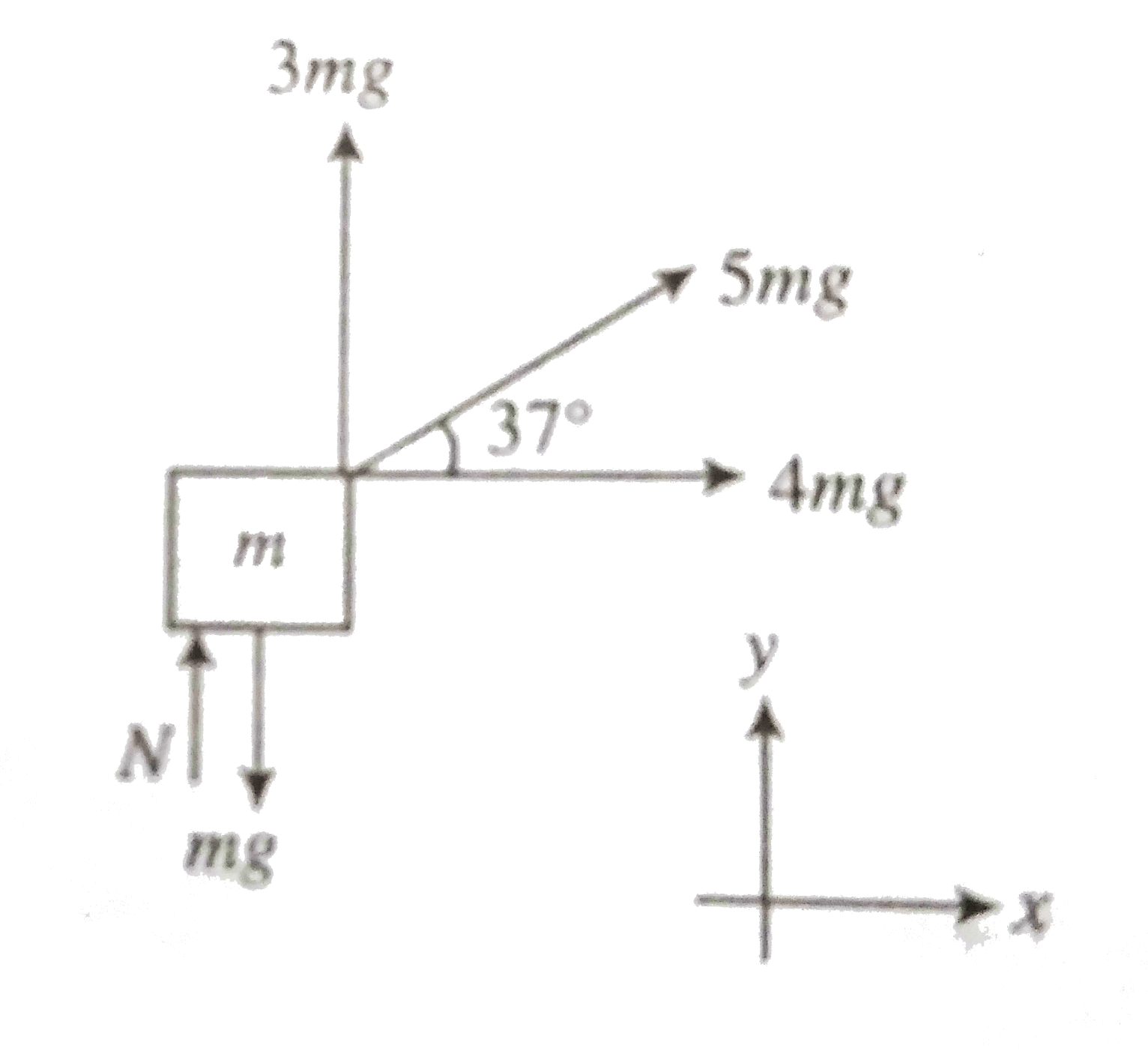
Resolving the forces along x- and y-axis, we have equation of motion.
ΣFx=max
4mg=max
This givesax=4g ...(i)
ΣFy=may
3mg−mg+N=may
2mg+N=may ..(iii)
Let ay=0.ThenN=−2mg
The nagative result signifies that N will be directed down (opposite to assumed direction), but the ground cannot pull the block down. Hence, the block will lose contact with the ground.
or N=0
Hence, from (ii) , ay=2g↑⏐
Hence, the acceleration , |→a|=√a2x+a2y
Where ax=4g form eq. (i) and ay=2g from eq. (ii)
This gives a=√a2x+a2y=√(4g)2+(20)2=2√5g .
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples11videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.111videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
A block of mass M is pulled on a smooth horizontal table by a string making an angle θ with the horizontal as shown in figure. If the acceleration of the block is a, find the force applied by the string and by the table N on the block.
 View Solution
View SolutionA block of mass m is placed at rest on a horizontal rough surface with angle of friction ϕ. The block is pulled with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
View SolutionA block of mass m is placed at rest on a horizontal rough surface with angle of friction ϕ. The block is pulled with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
View SolutionA block of mass m = 10 kg is pulled by a force F = 100 N at an angle θ=30∘ with the horizontal along a smooth horizontal surface. What is the acceleration of the block? (g=10m/s2)
 View Solution
View SolutionA block of mass M is pulled along a horizontal surface by applying a force at angle θ with the horizontal. The friction coefficient between the block and the surface is μ. If the block travels at a uniform velocity, find the work done by this applied force during a displacement d of the block.
View SolutionA block of mass M is pulled along a horizontal surface by applying a force at angle θ with the horizontal. The friction coefficient between the block and the surfasce is μ. If the block travels at a uniform velocity, find the work donen by this applied force during a displacement d of the blcok.
View SolutionA wooden block of mass M resting on a rough horizontal surface is pulled with a force T at an angle q to the horizontal. If m is coefficient of kinetic friction between the block and the surface, the acceleration of the block is
View SolutionA block of mass 10 kg is placed on the rough horizontal surface. A pulling force F is acting on the block which makes an angle θ above the horizontal. If coefficient of friction between block and surface is 43 then minimum value of force required to just move the block is (g=10ms2)
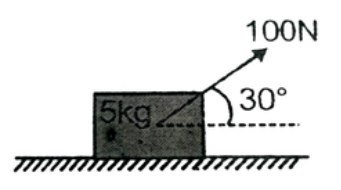
View SolutionA block of mass 5 kg is placed on a rough horizontal plane . The coefficients of stastic and kinetic friction between the block and surface are 0⋅5and0⋅3 respectively. A force of 100 N is applied at an angle 30∘ with the horizontal as shown in the figure . The acceleration of the block will be [ g = 10m/s2]
 View Solution
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m as shown in A horizontal force F is applied to one end of the rope. Find
(a) the acceleration of the rope and block
(b) the force that the rope exerts on the block
(c) the tension in the rope at its mid point
 View Solution
View Solution

