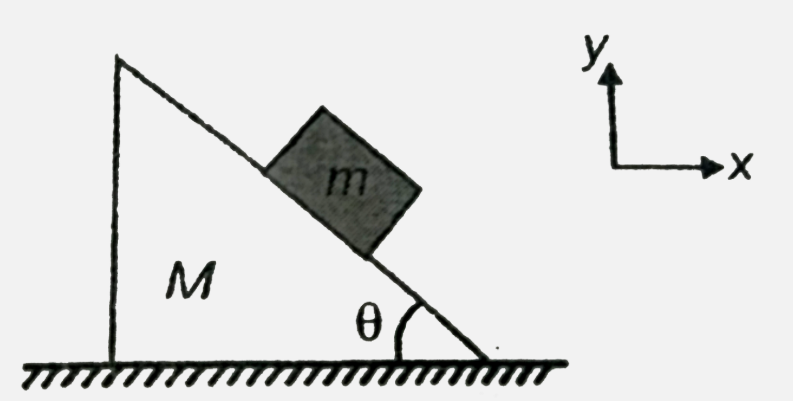
A block of mass m is placed on a triangular block of mass M(M=2m) , as shown. All surfaces are smooth. Calculate the velocity of triangular block when the smaller block reaches at bottom.

The correct Answer is:A
When the block reaches to the bottom of the wedge, their velocities are as shown in figure. Here v is the absolute veloctiy (with respect to ground), but vr is the relative velocity (relative to wedge).

Their absolute velocity components are as shown below:
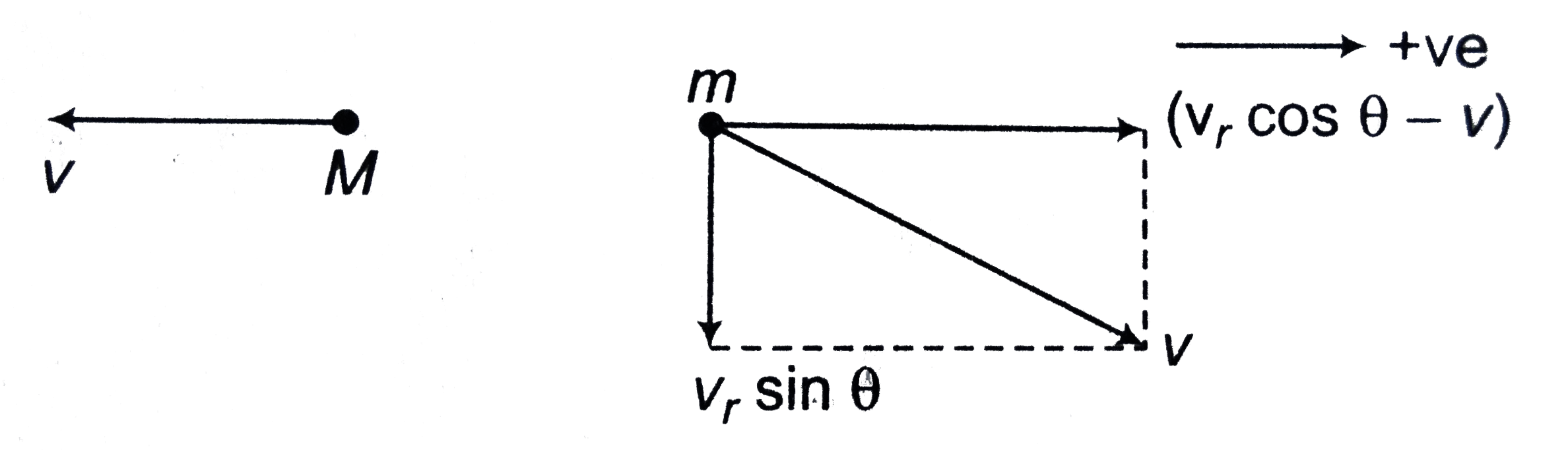
v=√(vrsinθ)2+(vrcosθ−v)2
Linear momentum in horizontal direction is conserved.
∴pi=pf
or 0=m(vrcosθ−v)−Mv ...(i)
Mechanical energy is also conserved.
Ei=Er
or mgh=12Mv2+12mv2
or mgh=12Mv2+12m[(v,sinθ)2+(vrcosθ−v)2] ...(ii)
We have two equations and two unknowns v and vr. Solving these equations, we can find the value of v.
Exercise: Solve these two equations to find the value of v.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - MiscellaneousExamples9videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.113videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Type 11videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions15videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery19videos
CIRCULAR MOTION
Similar Questions
Figure shows a small block of mass m which is started with a speed v on the horizontal part of the bigger block of mas m placed on a horizontal floor. The curved part of the surface shown is semicircular. All the surfaces are frictionless. Find the speed of the bigger block when the smaller block reaches the point A of the surface.
 View Solution
View SolutionA block of mass m is placed on a smooth wedge of mass M, as shown in the figure . Just after placiing block m over wedge M.
 View Solution
View SolutionA block of mass m is placed on a wedge of mass M and a force F is acting on its as shown . If all surfaces are smooth , find the force F such that, there is no relative motion between m and M.
 View Solution
View SolutionTwo blocks of mass M and m are kept on the trolley whose all surfaces are smooth select the correct statement
 View Solution
View SolutionA block of mass 1 kg is pushed towards another block of mass 2 kg from 6 m distance as shown in figure. Just after colision velocity of 2 kg block becomes 4 m//s
.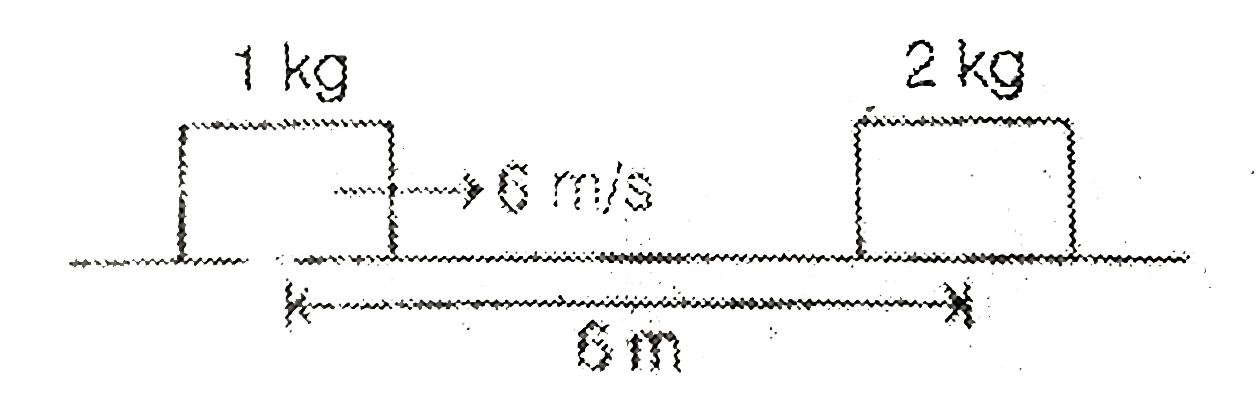 View Solution
View SolutionA block of mass m is placed on another block of mass M lying on a smooth horizontal surface as shown in the figure. The co-efficient of friction between the blocks is μ. Find the maximum horizontal force F (in Newton) that can be applied to the block M so that the blocks together with same acceleration? (M=3kg,m=2kg,μ=0.1,g=10m/s2)
 View Solution
View SolutionA block of mass M is placed on the top of a bigger block of mass 10 M as shown in figure. All the surfaces are frictionless. The system is released from rest, then the distance moved by the bigger block at the instant the smaller block reaches the ground :
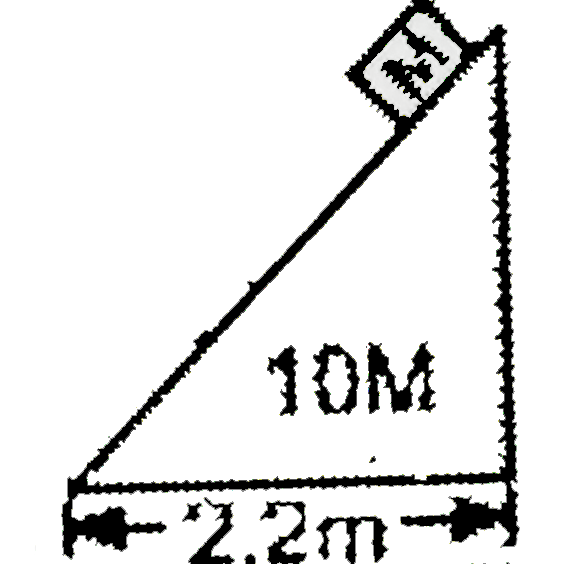 View Solution
View SolutionFigure shows a block A of mass 6m having a smooth semicircular groove of radius a placed on a smooth horizontal surface. A block B of mass m is released from a position in groove where its radius is horizontal. Find the speed of the bigger block when the smaller block reaches its bottom most position.
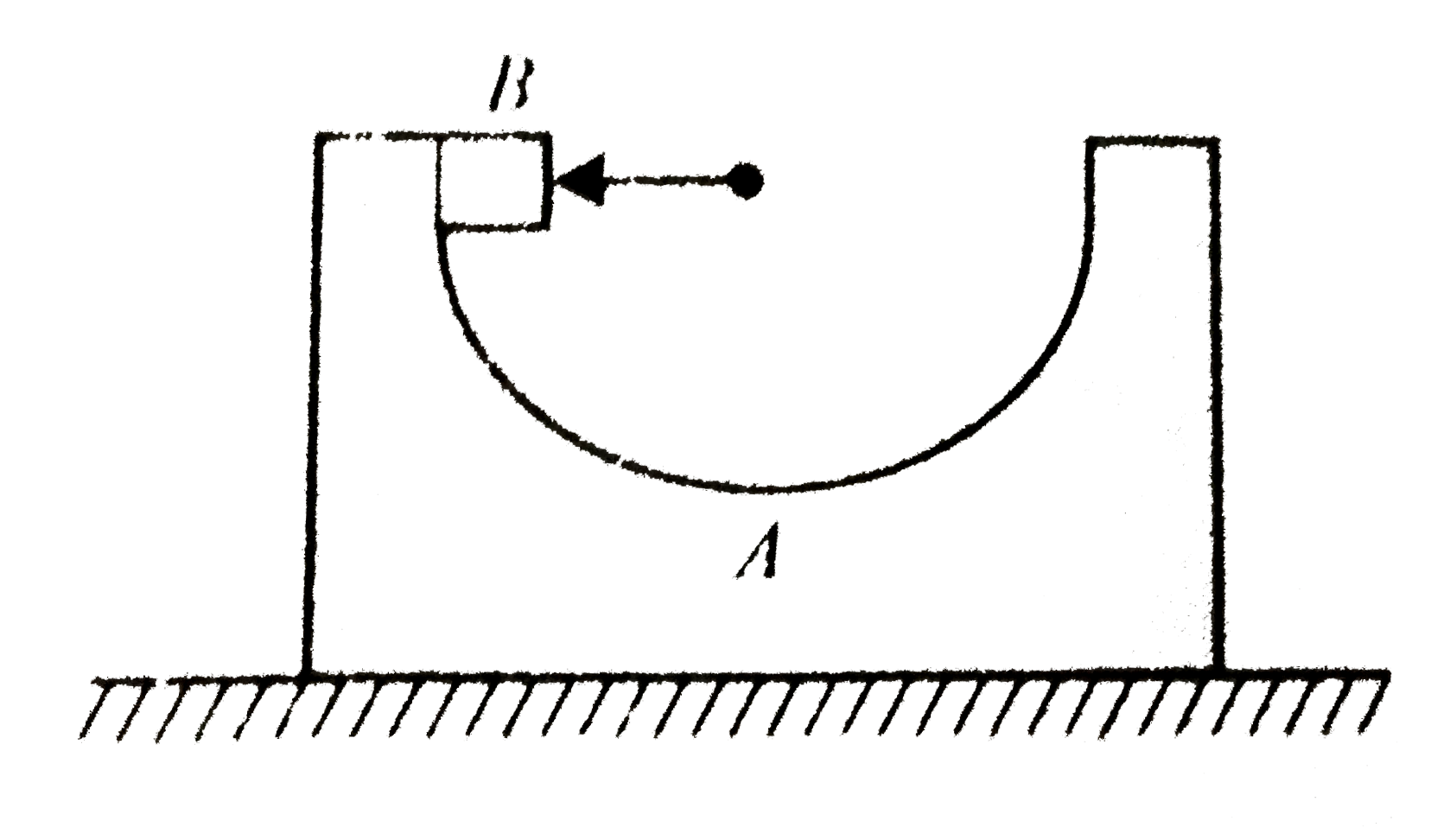 View Solution
View SolutionA block of mass m is placed on the inclined sufrace of a wedge as shown in fig. Calculate the acceleration of the wedge and the block when the block is released. Assume all surfaces are frictionless.
 View Solution
View SolutionA block of mass m is pushed towards a movable wedge of mass nm and height h, with a velocity u. All surfaces are smooth. The minimum value of u for which the block will reach the top of the wedge is
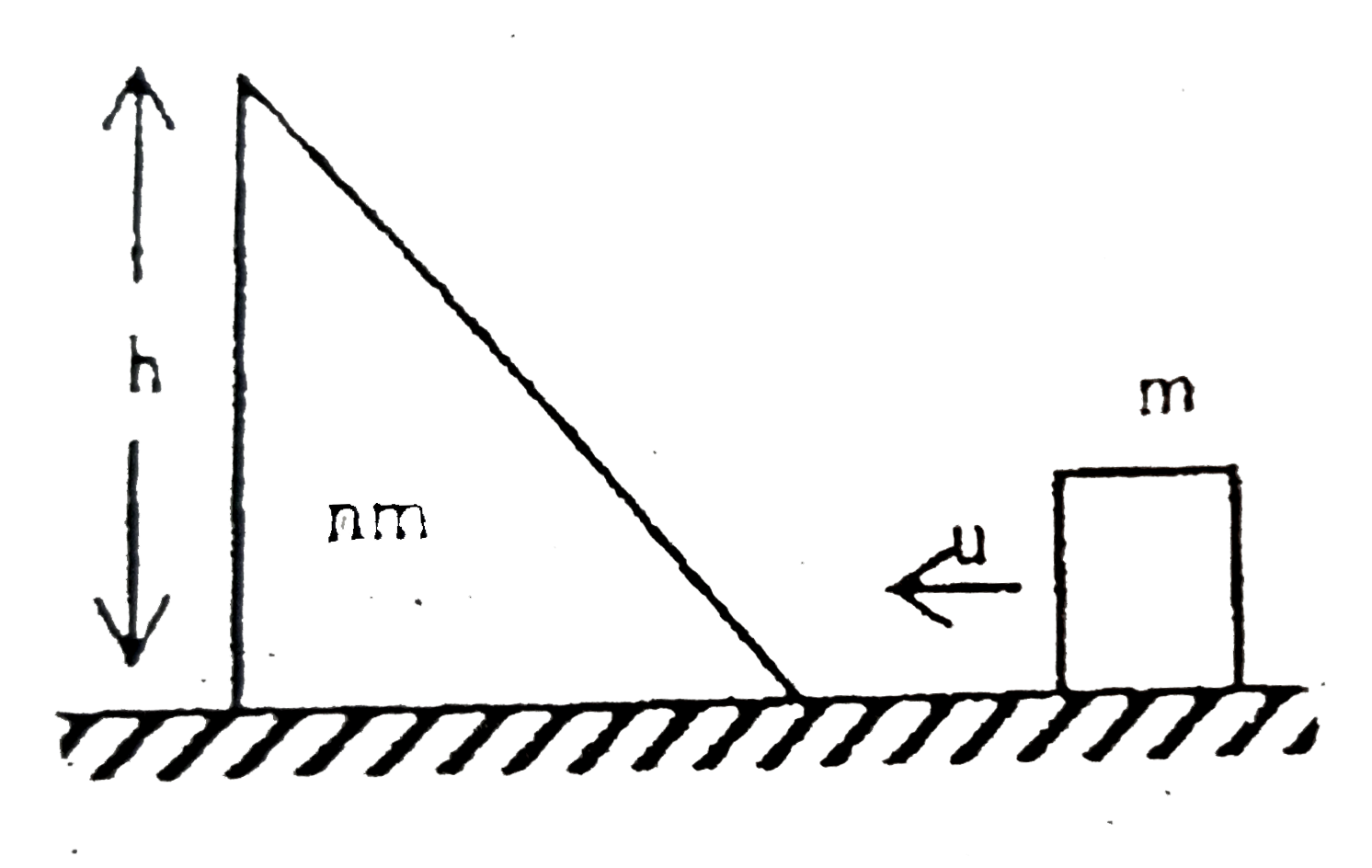 View Solution
View Solution
