A block of mass m is placed on an inclined plane. With what acceleration A towards right should the system move on a horizontal surface so that m does not slide on the surface of inclined plane? Also calculate the force supplied by wedge on the block. Assume all surfaces are smooth.
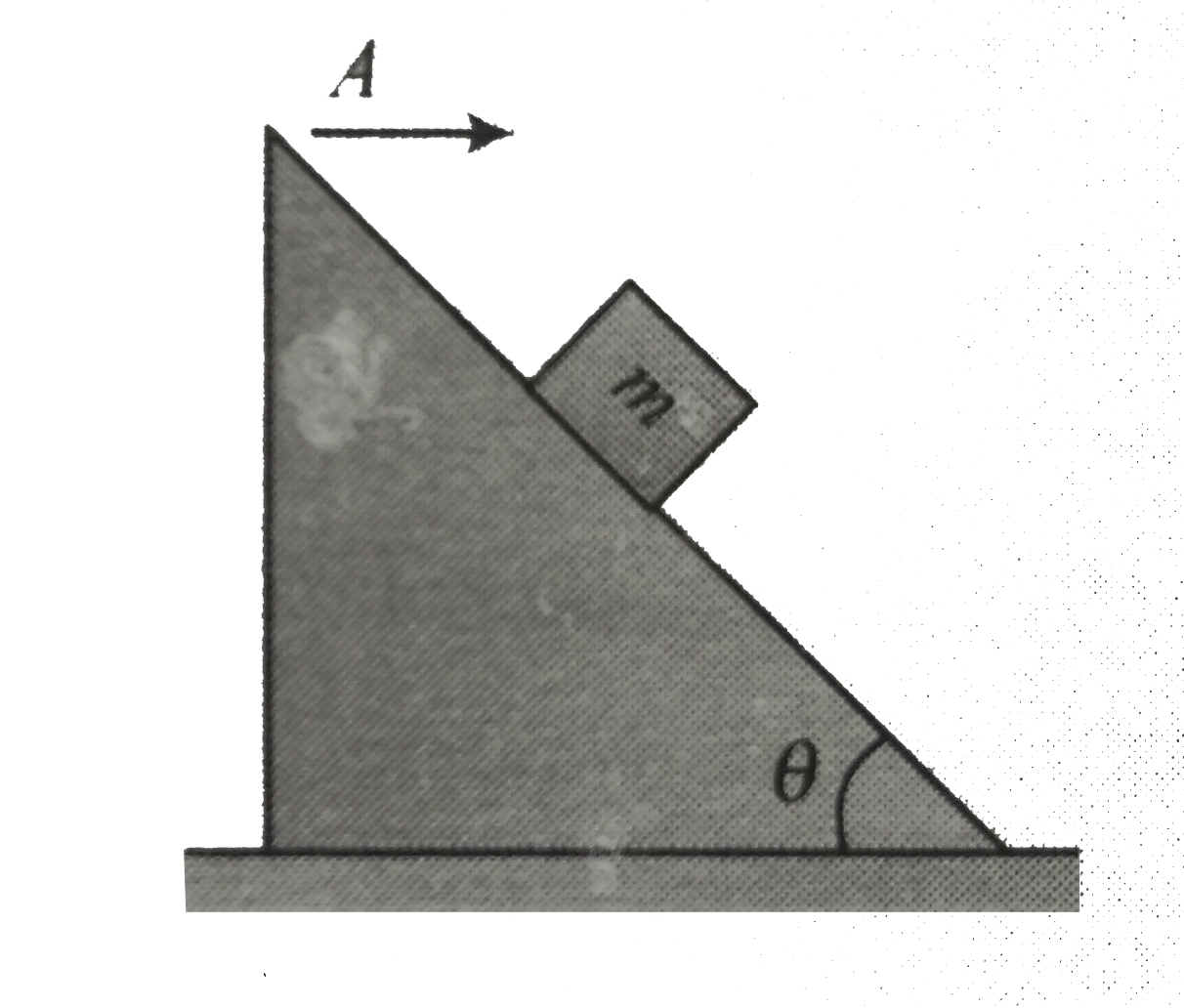
a=g(tanθ) , N=mgcosθ
a=g(sinθ) , N=gcosθ
a=−g(tanθ) , N=2mgcosθ
a=−g(tanθ) , N=3mg2cosθ
The correct Answer is:A
Method 1: Analysis of forces on m relative to ground
If the motion of m is analyzed from ground, its acceleration is A and the forces acting on it are its weight mg and normal reaction N.
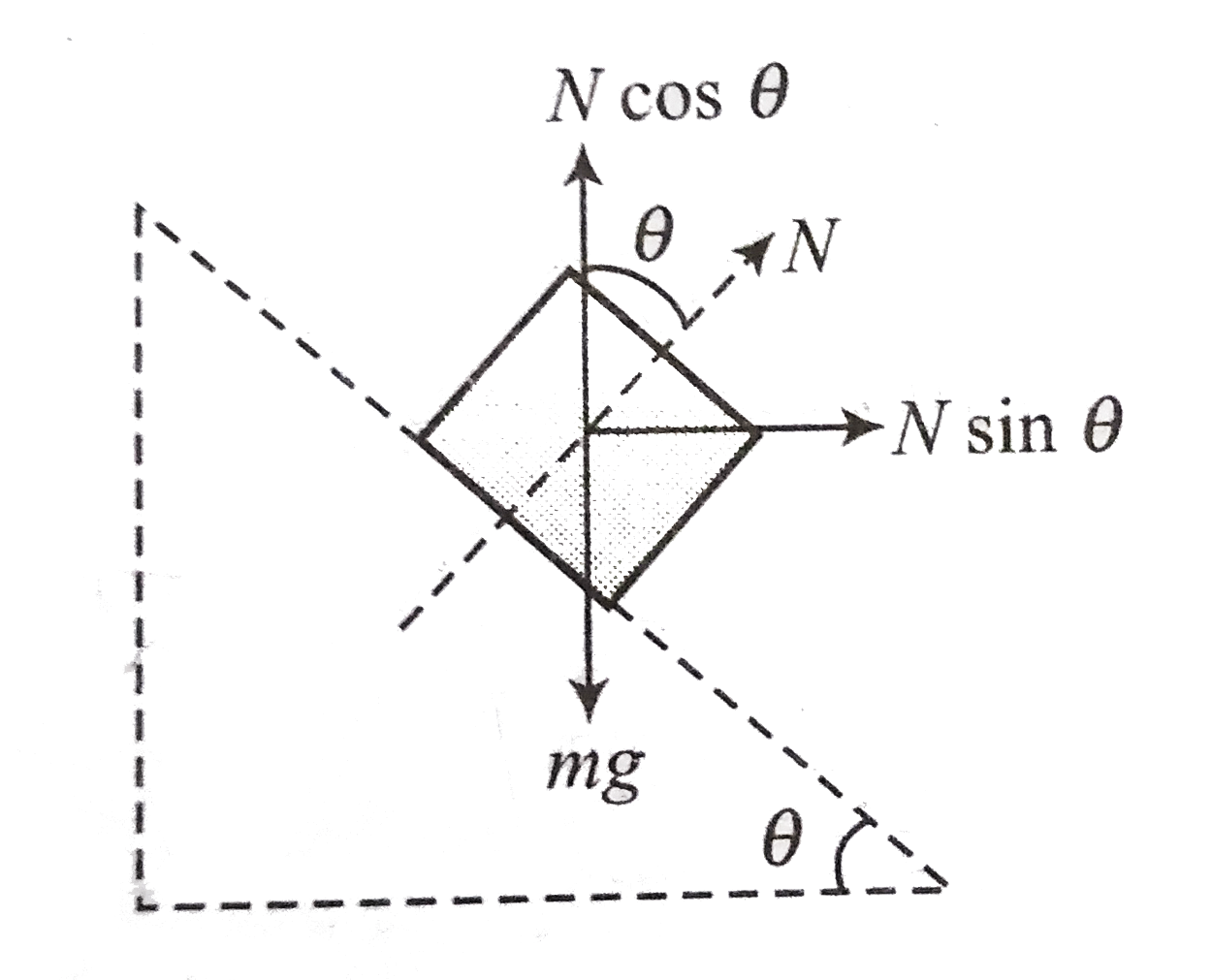
As m is at rest, moving with same acceleration as wedge in horizontal direction but in vertical direction. the block is at rest.
Σ→Fy=0⇒Ncosθ=mg...(i)
Σ→Fx=Σmi→ai⇒Nsinθ=mA ...(ii)
on solving (i) and (ii) we get A=gtanθandN=mgcosθ
Method 2: Analysis of forces on m relative to the inclined plane
If the motion of m is analyzed from the view point of an observer standing on the inclined plane (i.e., relative to the plane), its acceleration is 0 and the forces acting on it are : its weight, the normal reaction, and a pseudo force of magnitude mA towards left.
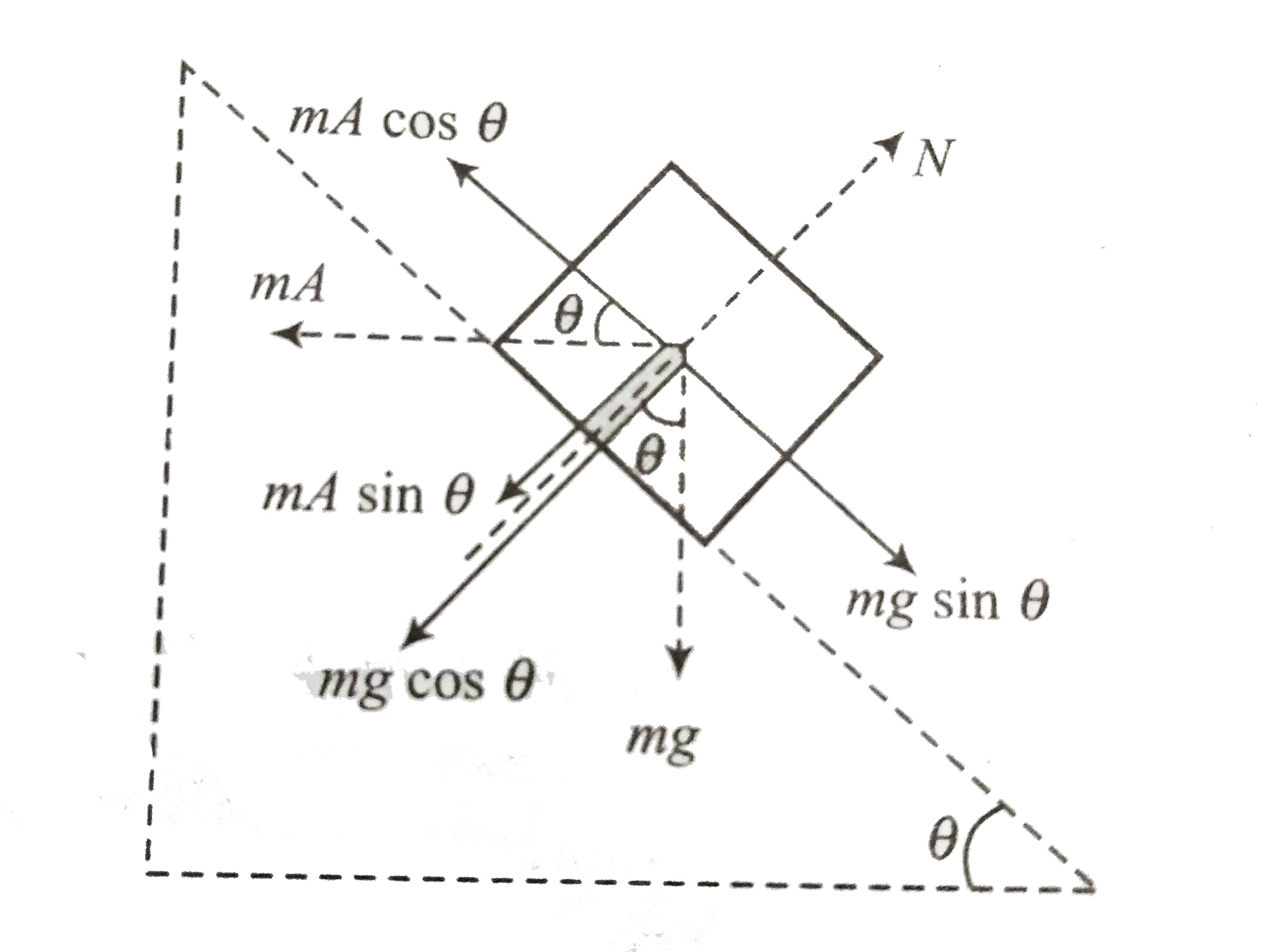
mAsinθ=mAcosθ
⇒A=gtanθ
Also: N=mgcosθ+mAsinθ
=mgcosθ+mgtanθsinθ=mgcosθ.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.1
11 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
A block of mass m is placed on a smooth wedge of inclination. The whole system is accelerated horizontally so that block does not slip on the wedge Find the i) Acceleration of the wedge Force to be applied on the wedge Force exerted by the wedge on the block .
View SolutionWhat force should be applied on the wedge so that block over it does not move? (All surfaces are smooth)

View Solution
Knowledge Check
A block of mass m is kept on an inclined plane of mass 2m and inclination α to horizontal. If the whole system is accelerated such that the block does not slip on the wedge then :
AThe normal reaction acting on 2m due to m is mgsecθBFor the block m to remain at rest with respect to wedge a force F=3mgtanα must be applied on 2mCThe normal reaction acting on 2m due to m is mgsecθDPseudo force acting on m with respect to ground is mgtanα towards west.A block mass 'm' is placed on a frictionless inclined plane of inclination θ with horizontal. The inclined plane is accelerated horizontally so that the block does not slide down. In this situation vertical force exerted by the inclined plane on the block is:
AmgsinθBmgcosθCmgDnone of theseA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
AmgBmgcosθCmgcosθDmgtanθ
A block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View SolutionA block is kept on a smooth inclined plane of angle of inclination θ that moves wuth a contact acceleration so that the block does not slide relative to the inclined plane. If the inclined plane stops the normal contact force offered by the plane on the block changes by a factor
View SolutionA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View SolutionA block of mass m is placed on a smooth wedge of inclination θ. The whole system is accelerated horizontally, so that the block does not slip on the wedge. The force exerted by the wedge on the block (g is acceleration due to gravity) will be
View SolutionA block is placed on an inclined plane. The block is moving towards right horizontal with an acceleration a0=g. The length of the inclined plane (AC) is equal to 1 m. Whole the situation are shown in the figure. Assume that all the surfaces are frictionless. The time taken by the block to reach from C to A is (Take,g=10m/s2)
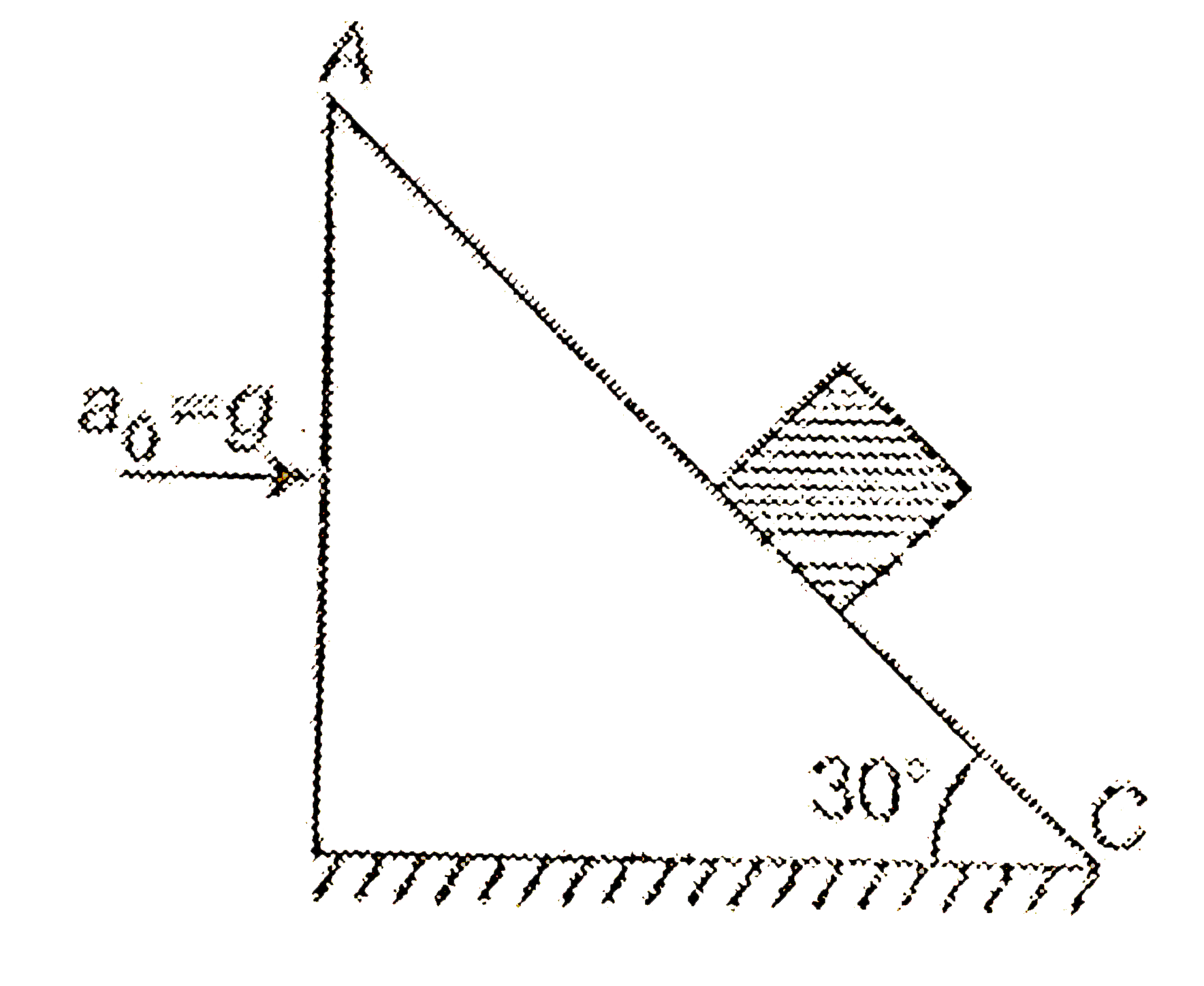
View Solution
