A block of mass m is placed on the inclined sufrace of a wedge as shown in fig. Calculate the acceleration of the wedge and the block when the block is released. Assume all surfaces are frictionless.

Constraint relation. Approach 1
We can observe that the wedge M can only move in horizontal direction towards left, and the block m can slide on inclined surface of M always in contact with the wedge.
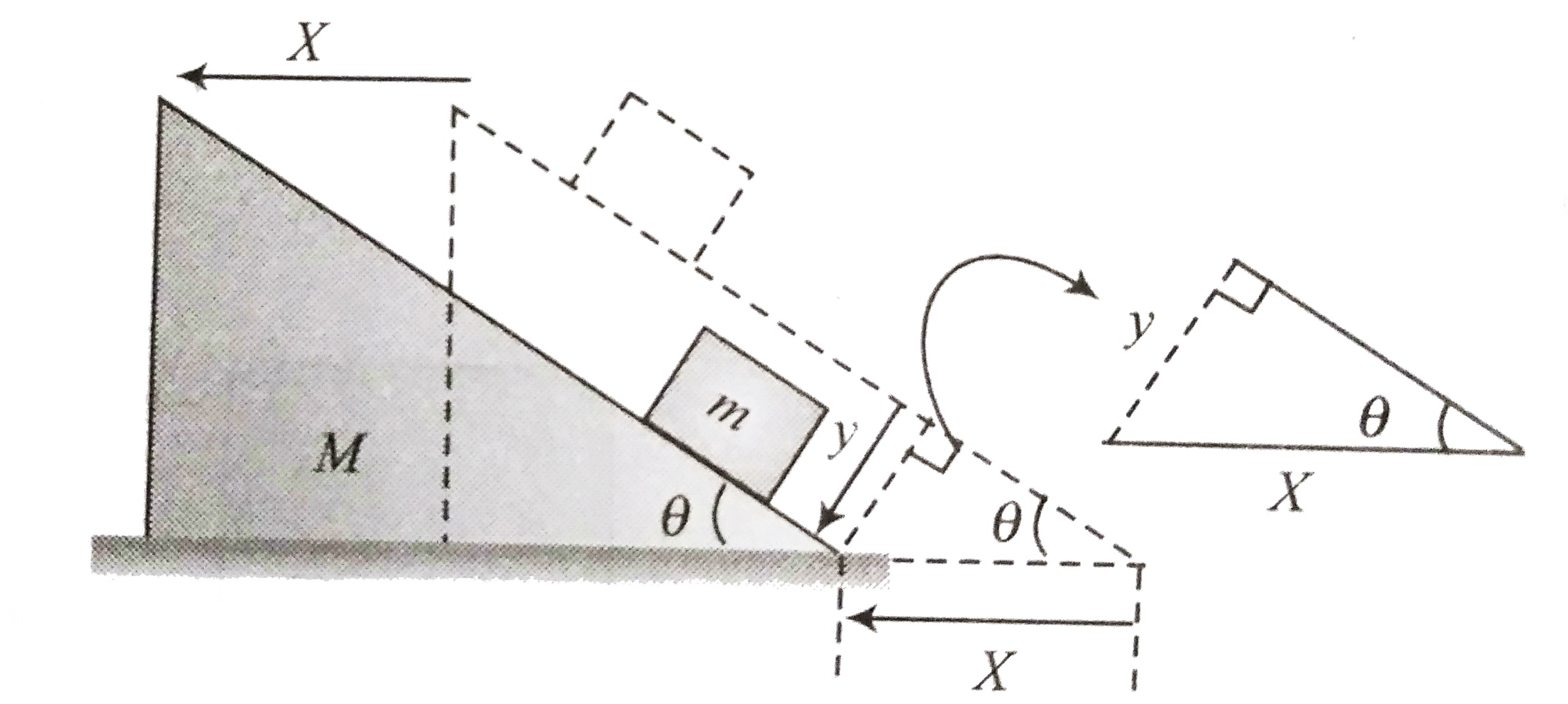
Let us define our x and y axes parallel to the incline and perpendicular to incline. respectively.
We can observe that the dispalcement of m and M in direction will be same as the block never lose contact with the wedge.
If the wedge moves in the horizontal direction by a distance x', during this time, the block will move x in x' direction.
We can relate these displacement x and X as
..(i)
Hence, velocity relation can be written as :
..(ii)
and acceleration relation can be written as:
..(iii)
Here and are the velocity and acceleration of the block, respectively, in the direction perpendicular to inclined surface.
Approach 2: We consider the motion of the block parallel to incline and perpendicular to inclined surface. Let the components of acceleration of block with respect to ground along these direction are and respectively.
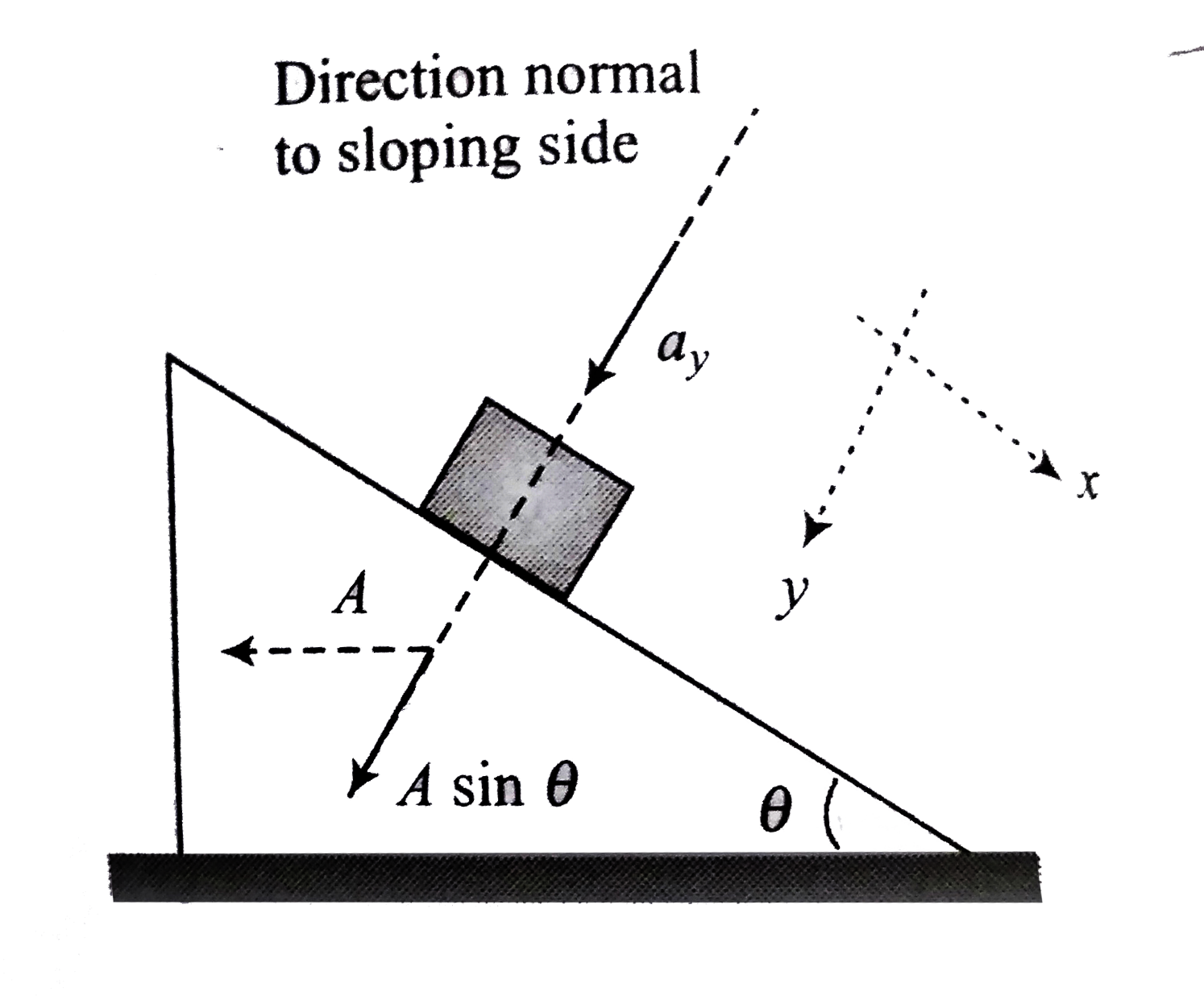
Then we can write
For wedge:
...(i)
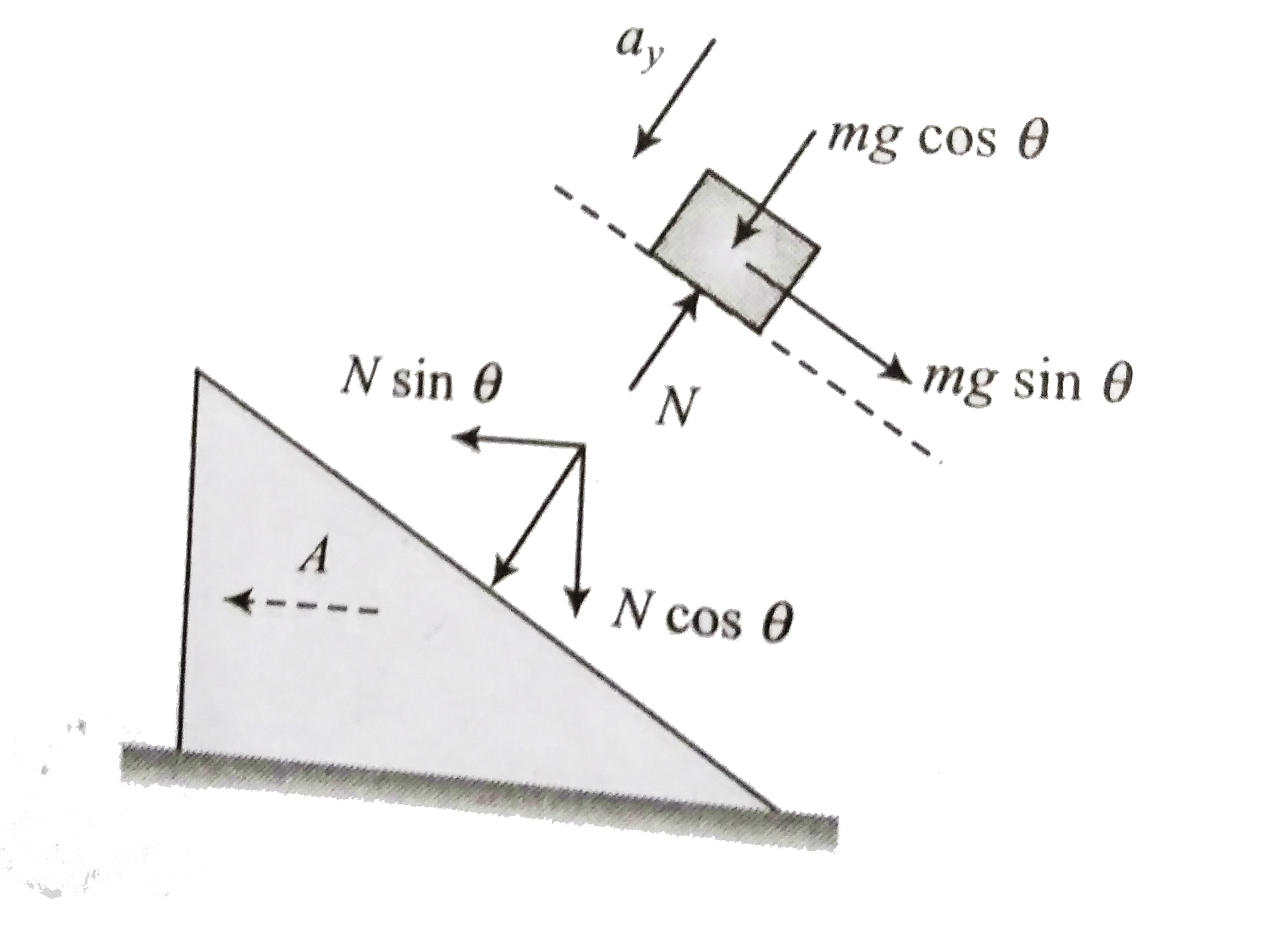
For block: Considering the block in the direction perpendicular to sloping surface.
but
Hence, ...(ii)
From (i) and (ii), we get
.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples11videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.111videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
A block of mass m is initially lying on a wedge of mass M with an angle of inclination θ as shown in figure. Calculate the displacement of the wedge when the block is released and reaches to the bottom of the wedge.
 View Solution
View SolutionA block is released on the convex surface of a hemispherical wedge as shown in Fig. Determine the displacement of the wedge when the block reaches the angular position θ
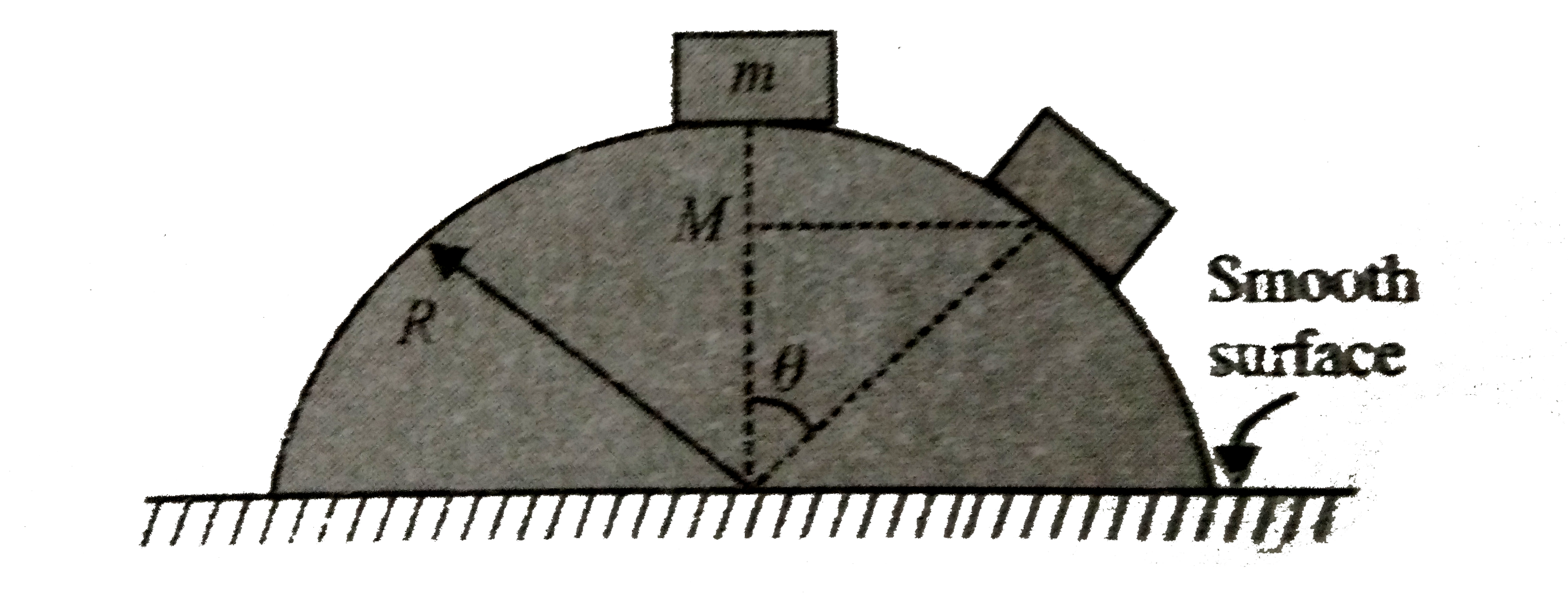 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In fig. mass m is being pulled on the incline of a wedge of mass M. All the surfaces are smooth. Find the acceleration of the wedge.
 Aa=F(1−cosθ)mg2sinθcosθM+2msin2θBa=F(1+cosθ)+mgsinθcosθM+msin2θCa=F(1−cosθ)−mgsinθcosθM+msin2θDa=F(1+cosθ)−mgsinθcosθM−msin2θ
Aa=F(1−cosθ)mg2sinθcosθM+2msin2θBa=F(1+cosθ)+mgsinθcosθM+msin2θCa=F(1−cosθ)−mgsinθcosθM+msin2θDa=F(1+cosθ)−mgsinθcosθM−msin2θ - Question 2 - Select One
A block of mass 1 kg is placed on a wedge shown in figure. Find out minimum coefficient of friction between wedge and block to stop the block on it.
 A0.6B0.9C1D0.2
A0.6B0.9C1D0.2
A block of mass m is at rest on a rought wedge as shown in figure. What is the force exerted by the wedge on the block?
 View Solution
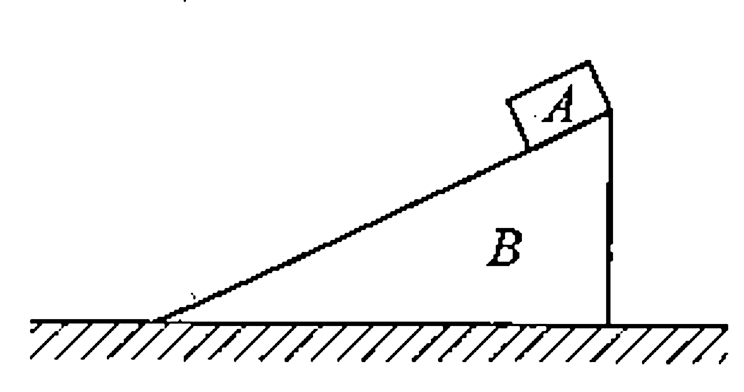
View SolutionA block A (mass 4M) is placed on the top of a wedge block B of base length l (mass=20M) as shown in figure. When the system is released from rest. Find the distance moved by the block B till the block A reaches ground Assume all surfaces are frictionless.
 View Solution
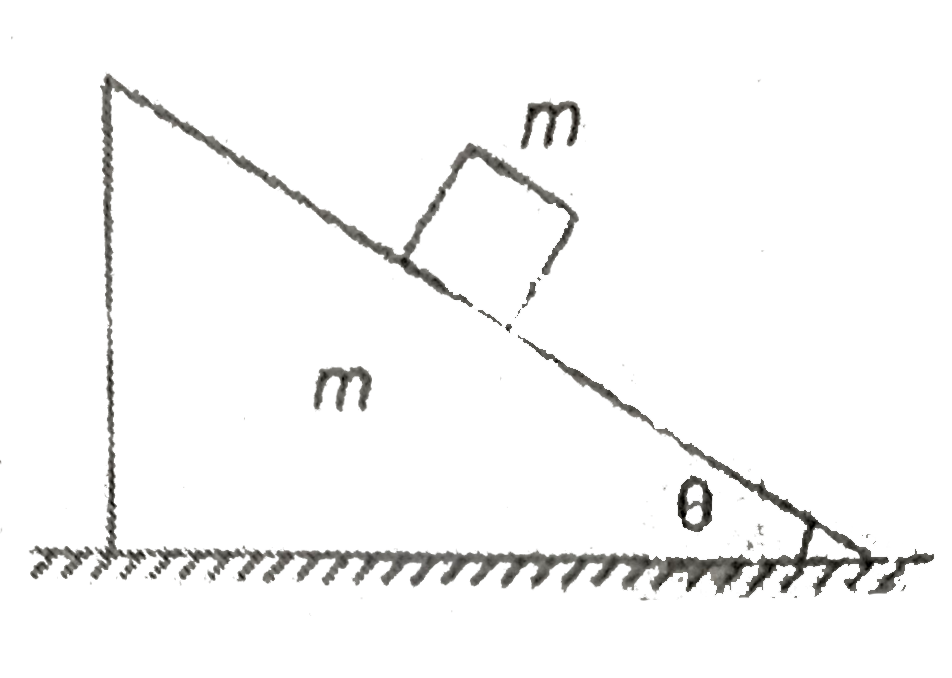
View SolutionA block of mass m slides down on inclined wedge of same mass m as shown in figure . Friction is absent everywhere . Acceleration of centre of mass of the block and wedge is
 View Solution
View SolutionA wedge of mass M makes an angle θ with the horizontal. The wedge is placed on horizontal frictionless surface. A small block of mass m is placed on the inclined surface of wedge. What horizontal force F must be applied to the wedge so that the force of friction between the block and wedge is zero ?
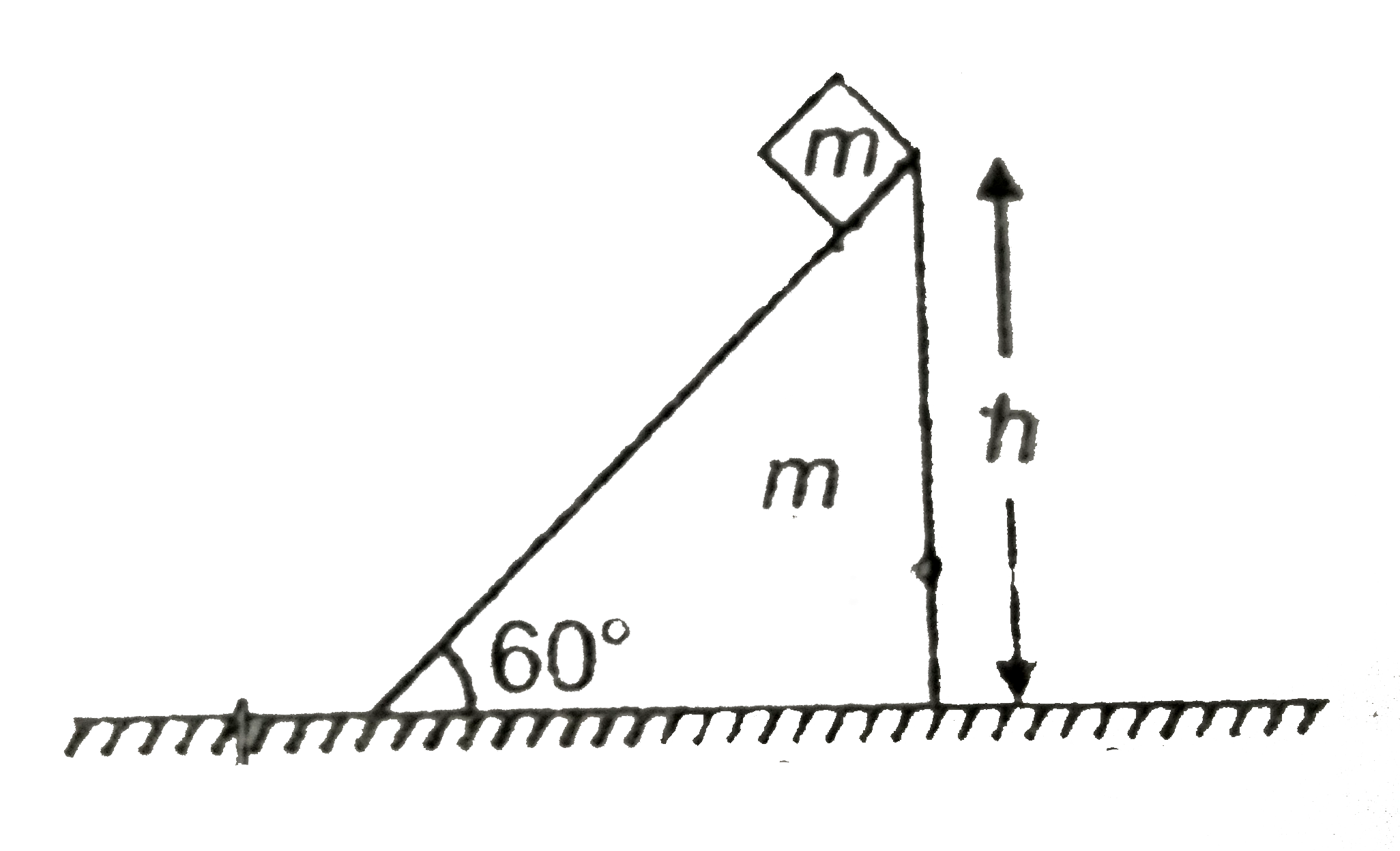
View SolutionA block of mass m is released from a wedge of mass m as shown in figure . Find the time taken by the block to reach the end of the wedge.
 View Solution
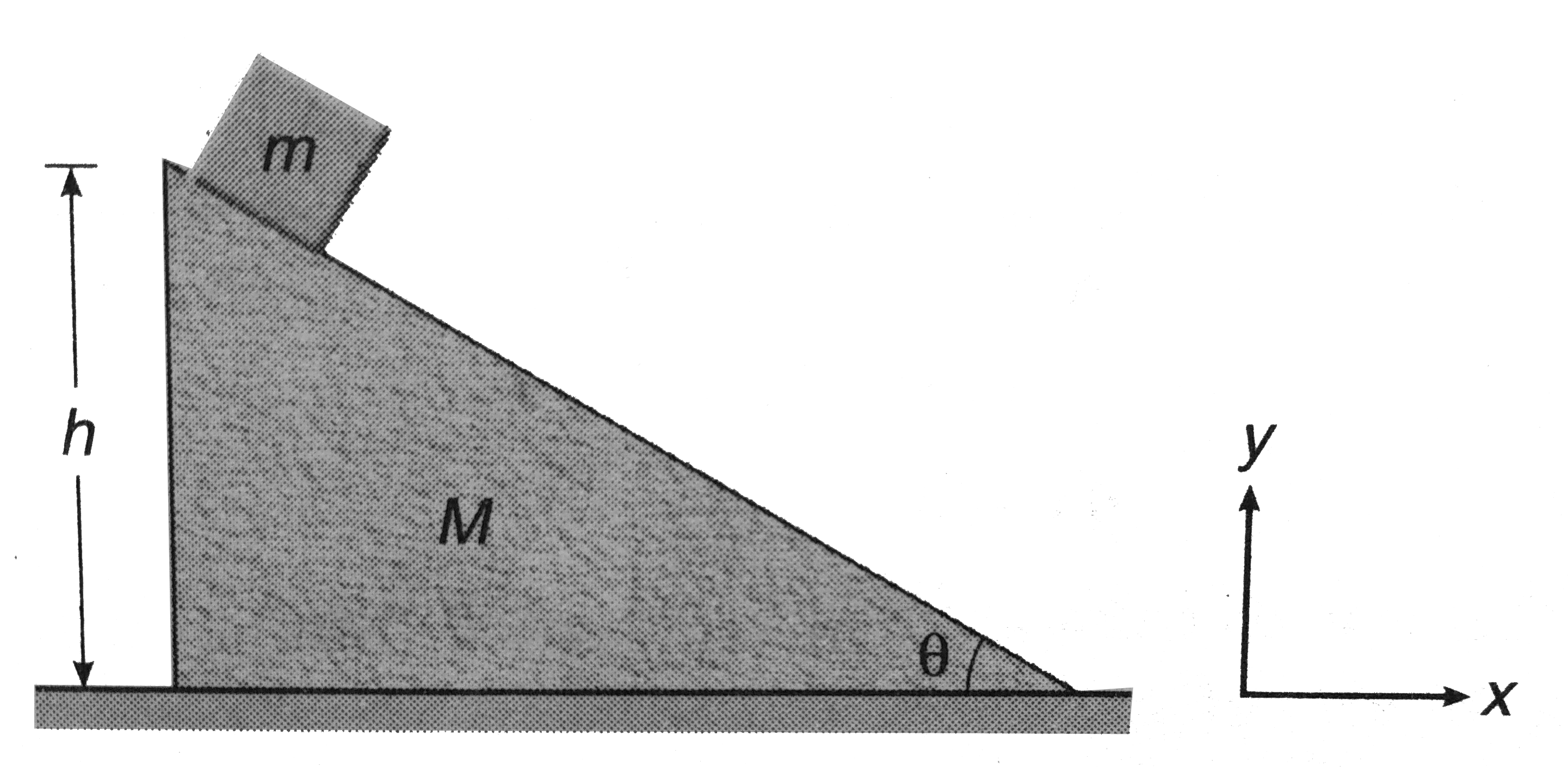
View SolutionA block of mass m is released from the top of a wedge of mass M as shown in figure. Find the displacement of wedges on the horizontal ground when the block reaches the bottom of the wedges. Neglect friction everywhere.
 View Solution
View Solution

