A block of mass m is pulled along a horizontal surface by applying a force at an angle θ with the horizontal. If the block travels with a uniform velocity and has a displacement d and the coefficient of friction is μ, then the work done by the applied force is
μmgdcosθ+μsinθ
μmgdcosθcosθ+μcosθ
μmgdsinθcosθ+μsinθ
μmgdcosθcosθ−μsinθ
The correct Answer is:B
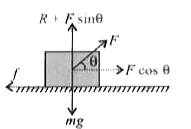
Because the block moves with a uniform velocity, the resultant force is zero. Resolving F into horizontal components Fcosθ and vertical component Fsinθ, we get
R+Fsinθ=mgorR=mg−Fsinθ
Also , f=μR=μ(mg−Fsinθ)
But f=Fcosθ
∴Fcosθ=μ(mg−Fsinθ) or F(cosθ+μsinθ)=μmg
or F=μmgcosθ+μsinθθ
work done, W=Fscosθ,W=μmgdcosθcosθ+μsinθ(∴s=d)
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - MTG GUIDECHAPTER - WORK, ENERGY AND POWEREXERCISE - NEET CAFE (TOPICWISE PRACTICE QUESTIONS) (KINETIC ENERGY)
18 Videos
- WORK, ENERGY AND POWERBOOK - MTG GUIDECHAPTER - WORK, ENERGY AND POWEREXERCISE - NEET CAFE (TOPICWISE PRACTICE QUESTIONS) (WORK - ENERGY THEOREM)
11 Videos
- WORK, ENERGY AND POWERBOOK - MTG GUIDECHAPTER - WORK, ENERGY AND POWEREXERCISE - AIPMT/NEET (MCQs)
34 Videos
- THERMODYNAMICSBOOK - MTG GUIDECHAPTER - THERMODYNAMICSEXERCISE - AIPMT/NEET (MCQs)
26 Videos
Similar Questions
A block of mass M is pulled along a horizontal surface by applying a force at angle θ with the horizontal. The friction coefficient between the block and the surface is μ. If the block travels at a uniform velocity, find the work done by this applied force during a displacement d of the block.
View SolutionA block of mass M is pulled along a horizontal surface by applying a force at angle θ with the horizontal. The friction coefficient between the block and the surfasce is μ. If the block travels at a uniform velocity, find the work donen by this applied force during a displacement d of the blcok.
View Solution
Knowledge Check
A block of mass m is lying on horizontal surface of coefficient of friction μ. A force is applied to the block at an angle θ with the horizontal. The block will move with a minimum force F if
Aμ=tanθBμ=cosθCμ=sinθDμ=cotθA block of mass m is placed on a rough horizontal surface. If minimum force to pull the block is mg2 then coefficient of friction is :
A12B√3C1√3DNoneA wooden block of mass M resting on a rough horizontal surface is pulled with a force F at an angle with the horizontal. If is the coefficient of kinetic friction between the block and the surface, then acceleration of the block is -
AFM(cosϕ+μsinϕ)−μgBFsin(ϕ)MCμFcosϕD,uFsinϕ
A block of mass M is pulled along a horizontal surface by applying a force at angle θ with the horizontal. The friction coefficient between the block and the surfasce is μ. If the block travels at a uniform velocity, find the work donen by this applied force during a displacement d of the blcok.
View SolutionA crate is pulled along a horizontal surface at constant velocity by an applied force F that makes an angle θ with the horizontal. The coefficient of kinetic friction between the crate and the surface is μ. Find the angle θ such that the applied force is minimum to slide the block. Also find the minimum value of this force.
View SolutionA block of mass m is placed at rest on a horizontal rough surface with angle of friction ϕ. The block is pulled with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
View SolutionA block of mass m is placed at rest on a horizontal rough surface with angle of friction ϕ. The block is pulled with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
View SolutionA block of mass M is being pulley along horizontal surface .The coefficient of friction the block and the surface is μ If another block of mass M/2 is placed on the block and it is pulled is again pulled on the surface , the coefficient of friction the block and the surface will be
View Solution
