A block of mass is released from point (A) in figure. The track is frictionless except for the position between points (B) and (C), which has a length of . The block travels down the track, hits a spring of force constant , and compresses the spring x from its equilibrium position before coming at rest momentarily. Determine the coefficient of kinetic friction between the block and the rough surface between (B) and (C).

Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.4
16 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.5
15 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.2
25 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA block slides down a curved frictionless track and then up an inclined plane as in figure. The coefficient of kinetic friction between the block and incline is μk. Find the maximum height reached by the clock.

View Solution
Knowledge Check

A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x thenAmgh=12kx2Bmg(h+x)=12kx2Cmgh=12k(x+h)2Dmg(h+x)=12k(x+h)2A block is suspended by an ideal spring of force constant force F and if maximum displacement of block from its initial mean position of rest is x0 then
Aincrease in energy stored in spring is kx20Bx0=3F2kCx0=2FkDwork done by applied force F is Fx0A spring, placed horizontally on a rough surface is compressed by a block of mass m, placed on the same surface so as to store maximum energy in the spring. If the coefficient of friction between the block and the surface is μ, the potential energy stored in the spring is
Aμ2m2g22kB2μm2g2kCμ2m2g2kD3μ2mg2k
A block of mass m = 1 kg is kept pressed against a spring on a rough horizontal surface. The spring is compressed by 10 cm from its natural length and to keep the block at rest in this position a horizontal force (F) towards left is applied. It was found that the block can be kept at rest if 8N≤F≤18N. Find the spring constant (k) and the coefficient of friction (μ) between the block and the horizontal surface.
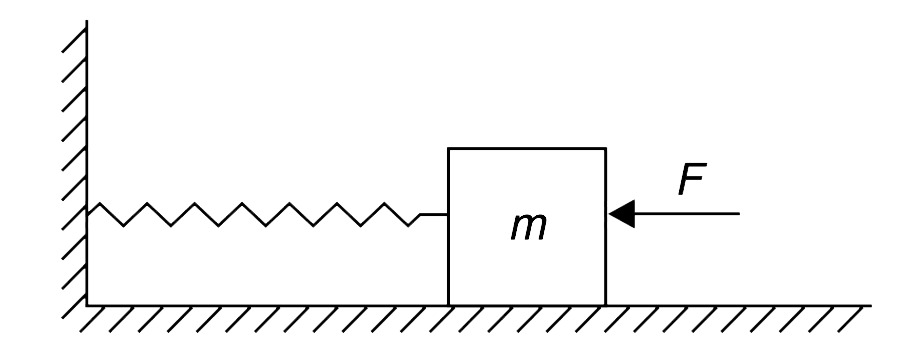
View SolutionA block of mass m slides from rest at a height H on a frictionless inclined plane as shown in the figure. It travels a distance d across a rough horizontal surface with coefficient of kinetic friction μ , and compresses a spring of spring k by a distance x before coming to rest momentarily. Then the spring extends and the block travels back attaining a final height of h. Then

View SolutionFigure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is

View SolutionA block with mass 0.50kg is forced against a horizontal spring of negligible mass , compressing the spring a distance of 0.20m (figure). When released, the block moves on a horizontal table top for 1.00N/m. What is the coefficient of kinetic friction μk, between the block and the block and the table?

View SolutionA block slides down a curved frictionless track and then up an inclined plane as in figure. The coefficient of kinetic friction between the block and incline is μk. Find the maximum height reached by the clock.

View Solution

