A child's pogo stick(figure) stores energy in a spring with a force constant of 2.5×104Nm. At position (A) (xA=0.10m), the spring compression is a maximum and the child is momentarily at rest. At position (B) (xB=0), the spring is relaxed and the child is moving upward. At position (C), the child is again momentarily at rest at the top of the jump. The combined mass of child and pogo stick is 25kg. (a) Calculate the total energy of the child-stick-earth system if both gravitational and elastic potential energies are zero for x=0. (b) Determine xC. (c) Calculate the speed of the child at x=0. (d) Determine the value of x for which the kinetic energy of the system is a maximum. (e) Calculate the child's maximum upward speed.
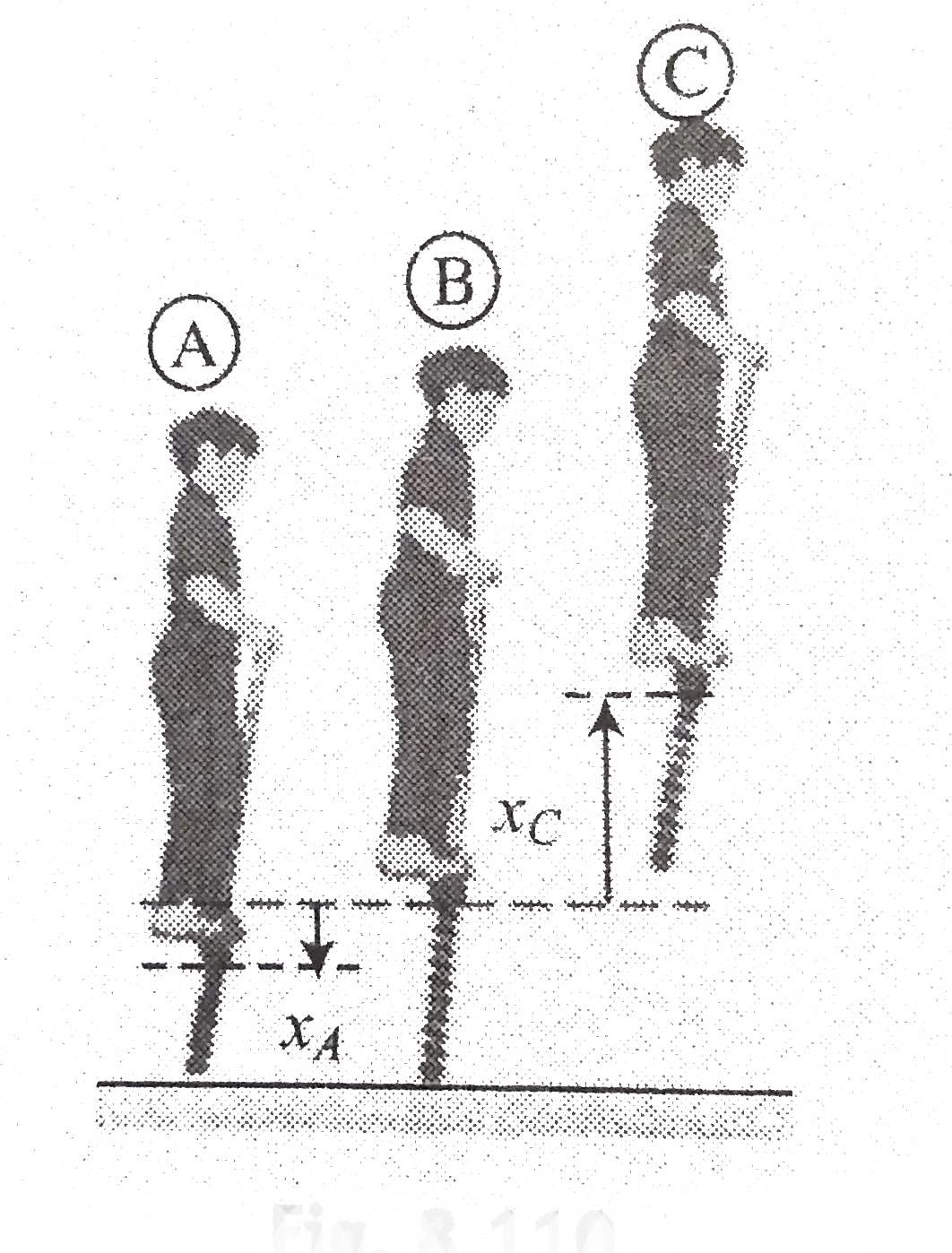
k=2.5×104Nm−1, m=25kg, XA=−0.10m,
Ug∣∣x=0=Us∣∣x=0=0
a. Emech=KA+UgA+UsA=0+mgxA+12kx2A
=25×10×(−0.100)+12×2.5×104×(−0.100)2
=−25J+125J=100J
b. Since only conservation forces are involved, the total energy of the child-pogo stick-earth system at point C is the same as that at point A.
KC+UgC+UsC=KA+UgA+UsA
0=25×10×xC+0=0−25J+125J
xC=0.40m
c. KB+UgBB+UsB=KA+UgA+UsA
12×25×v2B+0+0=0+(−25)+125
vB=2√2ms−1
d. K and v are at a maximum when a=∑F/m=0 (i.e., when the magnitude of the upward spring force equals the magnitude of the downward gravitational force).
This occurs at x<0, where k|x|=mg.
|x|=25×102.5×104=10×10−3m=10mm
Thus, K=Kmax at x=−10mm
e. 12×25×v2max=25×10×[(−0.100)−(−0.01)]+12(25×104)[(−0.100)2−(−0.01)2]
⇒vmax=2.85ms−1
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.4
16 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.5
15 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.2
25 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A spring block system is placed on a rough horizontal floor. Force constant of the spring is k. The block is pulled to right to give the spring an elongation equal to x0 and then it is released. The block moves to left and stops at the position where the spring is relaxed. Calculate the maximum kinetic energy of the block during its motion.
View SolutionA body of mass 0.1 g moving with a velocity of 10 m/s hits a spring (fixed at the other end) of force constant 1000 N/m and comes to rest after compressing the spring. The compression of the spring is
View Solution
Knowledge Check
The diagram shows the various positions of a child in motion on a swing. Somewhere in front of the child a stationary whistle is blowing.
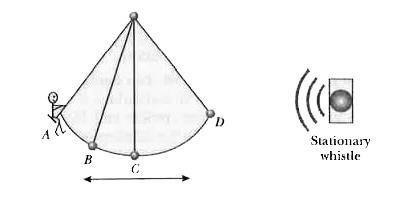
At which position(s) will the child hear the highest frequency for the sound from the whistle?AAt both A and D.BAt C when moving toward BCAt B when moving toward A.DAt C when moving toward DThe diagram shows the various positions of a child in motion on a swing. Somewhere in front of the child a stationary whistle is blowing.
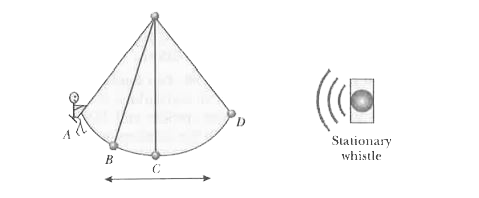
At which position(s) will the child hear the lowest frequency for the sound from the whistle?AAt both A and D.BAt C when moving toward BCAt B when moving toward ADAt C when moving toward D.A body of mass 0.1 g moving with a velocity of 10 m/s hits a spring (fixed at the other end) of force constant 1000 N/m and comes to rest after compressing the spring. The compression of the spring is
A0.01 mB0.1 mC0.2 mD0.5 m
A flat car of mass M with a child of mass m is moving with a velocity v1. The child jumps in the direction of motion of car with a velocity u with respect to the car. Find the final velocities of the child and that of the car after jump.
View SolutionA collar B of mass m is at rest and when it is in the position shown, the spring is unstretched. If another collar A of mass mn strikes it so that B slides a distance 4m on the smooth rod before momentarily stopping, determine the velocity of A just after the impact. The coefficient of restitution is e. The spring constant is k.
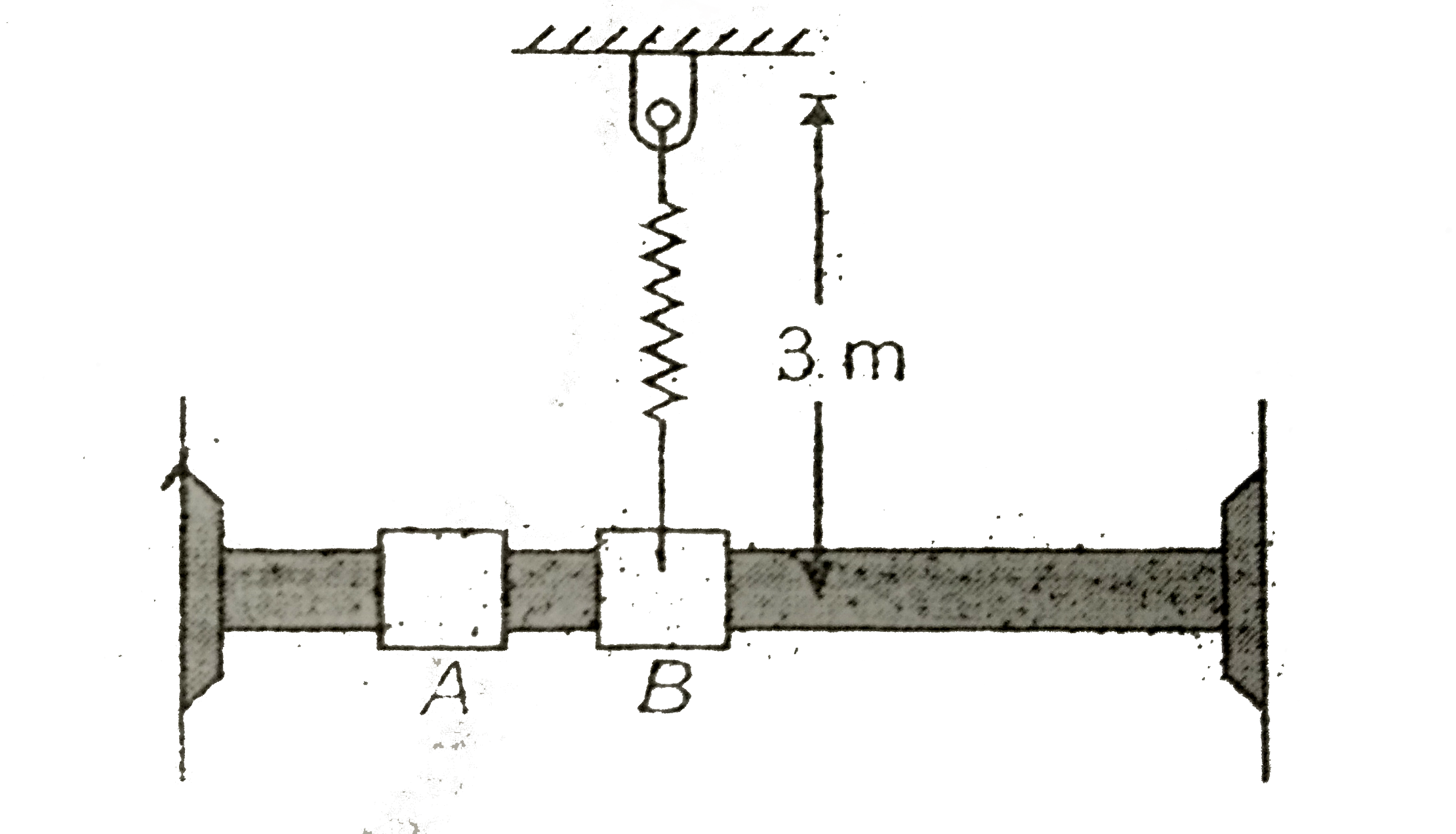
View SolutionIf a body of mass m suspended by a spring comed to rest after a downward displecemtn y0, claculate (a) force constant of the spring, (b) loss in gravitational potential energy, (c) gain in elastic potential energy of spring.
View Solution
A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x then
View SolutionA massless spring with a force constant K=40N/m hangs vertically from the ceiling.A 0.2kg block is attached to the end of the spring and held in such a position that the spring has its natural length and suddenyl released. The maximum elastic strain energy stored in the spring is (g=10m/s2)
View Solution
