A block of mass m is released from rest at a height R above a horizontal surface. The acceleration due to gravity is g. The block slides along the inside of a frictionless circular hoop of radius R.
Which one of the following expressions gives the speed of the mass at the bottom of the hoop ?
zerom/s2
v=mg2R
v2=2gR
v=mgR
The correct Answer is:C
To solve the problem of finding the speed of a block of mass m at the bottom of a frictionless circular hoop of radius R, we can use the principle of conservation of mechanical energy. Here’s a step-by-step solution:
Step 1: Understand the Initial and Final Conditions
- The block is released from rest at a height R above the horizontal surface.
- At the top (initial position), the block has potential energy and no kinetic energy since it starts from rest.
- At the bottom (final position), the block has kinetic energy and no potential energy (as it is at the reference height).
Step 2: Write the Expression for Potential Energy at the Top
The potential energy (PE) at the top when the block is at height R is given by:
PEtop=mgh=mgR
where h=R and g is the acceleration due to gravity.
Step 3: Write the Expression for Kinetic Energy at the Bottom
The kinetic energy (KE) at the bottom when the block has speed v is given by:
KEbottom=12mv2
Step 4: Apply the Conservation of Energy Principle
According to the conservation of mechanical energy, the total mechanical energy at the top must equal the total mechanical energy at the bottom:
PEtop=KEbottom
Substituting the expressions we derived:
mgR=12mv2
Step 5: Simplify the Equation
We can cancel the mass m from both sides (assuming m≠0):
gR=12v2
Step 6: Solve for v2
To isolate v2, multiply both sides by 2:
2gR=v2
Step 7: Take the Square Root to Find v
Taking the square root of both sides gives us the speed v at the bottom of the hoop:
v=√2gR
Final Expression
Thus, the speed of the mass at the bottom of the hoop is:
v=√2gR
- The block is released from rest at a height R above the horizontal surface.
- At the top (initial position), the block has potential energy and no kinetic energy since it starts from rest.
- At the bottom (final position), the block has kinetic energy and no potential energy (as it is at the reference height).
The potential energy (PE) at the top when the block is at height R is given by:
PEtop=mgh=mgR
where h=R and g is the acceleration due to gravity.
The kinetic energy (KE) at the bottom when the block has speed v is given by:
KEbottom=12mv2
According to the conservation of mechanical energy, the total mechanical energy at the top must equal the total mechanical energy at the bottom:
PEtop=KEbottom
Substituting the expressions we derived:
mgR=12mv2
We can cancel the mass m from both sides (assuming m≠0):
gR=12v2
To isolate v2, multiply both sides by 2:
2gR=v2
Taking the square root of both sides gives us the speed v at the bottom of the hoop:
v=√2gR
Thus, the speed of the mass at the bottom of the hoop is:
v=√2gR
Topper's Solved these Questions
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Matrix-Match)
1 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (More than one choice correct type)
10 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)
4 Videos
Similar Questions
A particle is taken to a height R above the earth's surface, where R is the radius of the earth. The acceleration due to gravity there is
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View Solution
Knowledge Check
A block of mass m is released from rest at a height R above a horizontal surface. The acceleration due to gravity is g. The block slides along the inside of a frictionless circular hoop of radius R.
What is the magnitude of the normal force exerted on the block by the hoop when the block has reached the bottom ?AmgB3mgCmg2RD2mgThe ratio of acceleration due to gravity at a height 3 R above earth's surface to the acceleration due to gravity on the surface of earth is
(R = radius of earth)A1/9B1/16C1/4D1/3The ratio of acceleration due to gravity at a height 3R above earth 's surface to the acceleration due to gravity on the surface of the earth is (where R=radius of earth)
A19B14C116D13
A block of mass m slides along a frictionless surfce as shown in the figure. If it is releases from rest t A what is its speed at B?

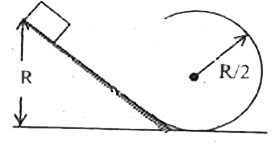
View SolutionA block of mass m is released from a height R on the frictionless incline as shown. The incline leads to a circle of radius R/2. The maximum height attained by the block is
View SolutionA satellite of mass m revolves around the earth of radius R at a height x from its surface. If g is the acceleration due to gravity on the surface of the earth, the orbital speed of the satellite is
View SolutionA body of mass m rises to a height h=R/5 from the surface of earth. If g is the acceleration due to gravity at the surface of earth, the increase in potential energy is (R = radius of earth)
View SolutionA block of mass m is released from the top of a mooth inclined plane of height h its speed at the bottom of the plane is proportion to
View Solution
