Question

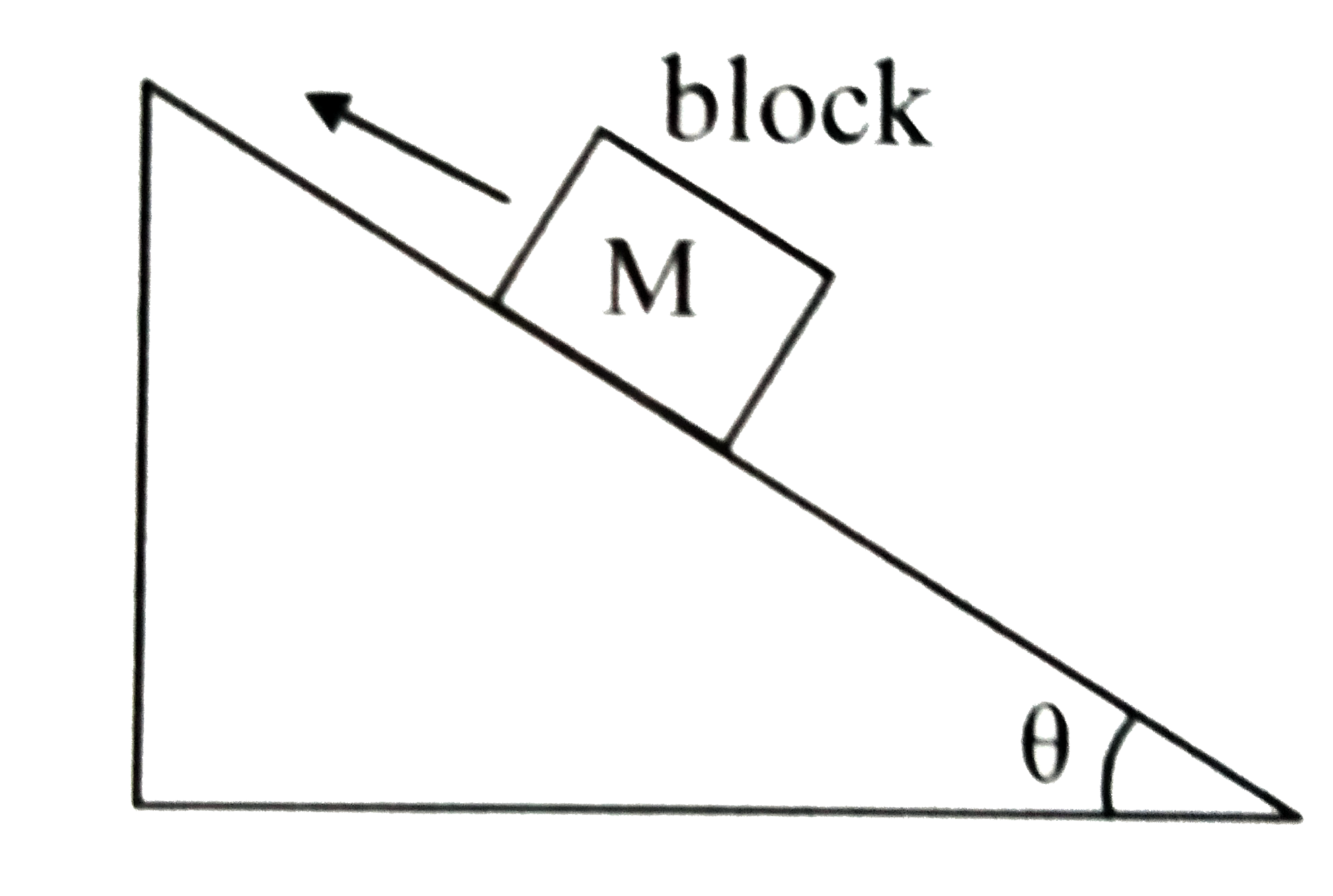
A block of mass m is sliding down an inclined plane with uniform velocity v. Angle that the plane makes with the horizontal is $\theta$. Assume edge of the cube to be a, calculate torque of the normal reaction about the centre of the block.

Options

A. `(1)/(2)mga cos theta`
B. `(1)/(2)mga sin theta`
C. mga
D. zero

Answer

B

Explanation

To solve the problem of calculating the torque of the normal reaction about the center of the block sliding down an inclined plane, we can follow these steps:

Step 1: Understand the Forces Acting on the Block
The block of mass \( m \) is sliding down the inclined plane at an angle \( \theta \) with uniform velocity \( v \). Since the block is moving with uniform velocity, the net force acting on it along the incline must be zero. The forces acting on the block include:
- The gravitational force \( mg \) acting downwards.
- The normal force \( N \) acting perpendicular to the inclined plane.
- The frictional force \( f \) acting up the incline.

Step 2: Resolve the Gravitational Force
We can resolve the gravitational force \( mg \) into two components:
- The component parallel to the incline: \( mg \sin \theta \)
- The component perpendicular to the incline: \( mg \cos \theta \)

Step 3: Apply Newton's Second Law
Since the block is sliding with uniform velocity, the acceleration is zero. Thus, we can write the equation for forces along the incline:
\( mg \sin \theta - f = 0 \implies f = mg \sin \theta \)
This indicates that the frictional force equals the component of the gravitational force acting down the incline.

Step 4: Calculate the Torque due to Friction
The torque \( \tau_f \) due to the frictional force about the center of the block can be calculated as:
\( \tau_f = f \cdot d \)
where \( d \) is the perpendicular distance from the line of action of the frictional force to the center of mass of the block. Since the block is a cube with edge length \( a \), the distance from the center of the block to the point where the friction acts (at the bottom edge) is \( \frac{a}{2} \). Therefore:
\( \tau_f = f \cdot \frac{a}{2} = (mg \sin \theta) \cdot \frac{a}{2} \)

Step 5: Calculate the Torque due to Normal Force
The normal force \( N \) acts perpendicular to the inclined plane. Since the normal force acts at the center of the block, its torque about the center of mass is zero. However, it must balance the torque due to friction to maintain equilibrium.

Step 6: Conclusion
The torque of the normal reaction about the center of the block is equal to the torque due to friction, which is:
\( \tau_N = \tau_f = mg \sin \theta \cdot \frac{a}{2} \)

Final Answer
Thus, the torque of the normal reaction about the center of the block is:
\( \tau_N = \frac{mg \sin \theta \cdot a}{2} \)