A block of mass m is suddenly released from the top of a spring of stiffness constant k.
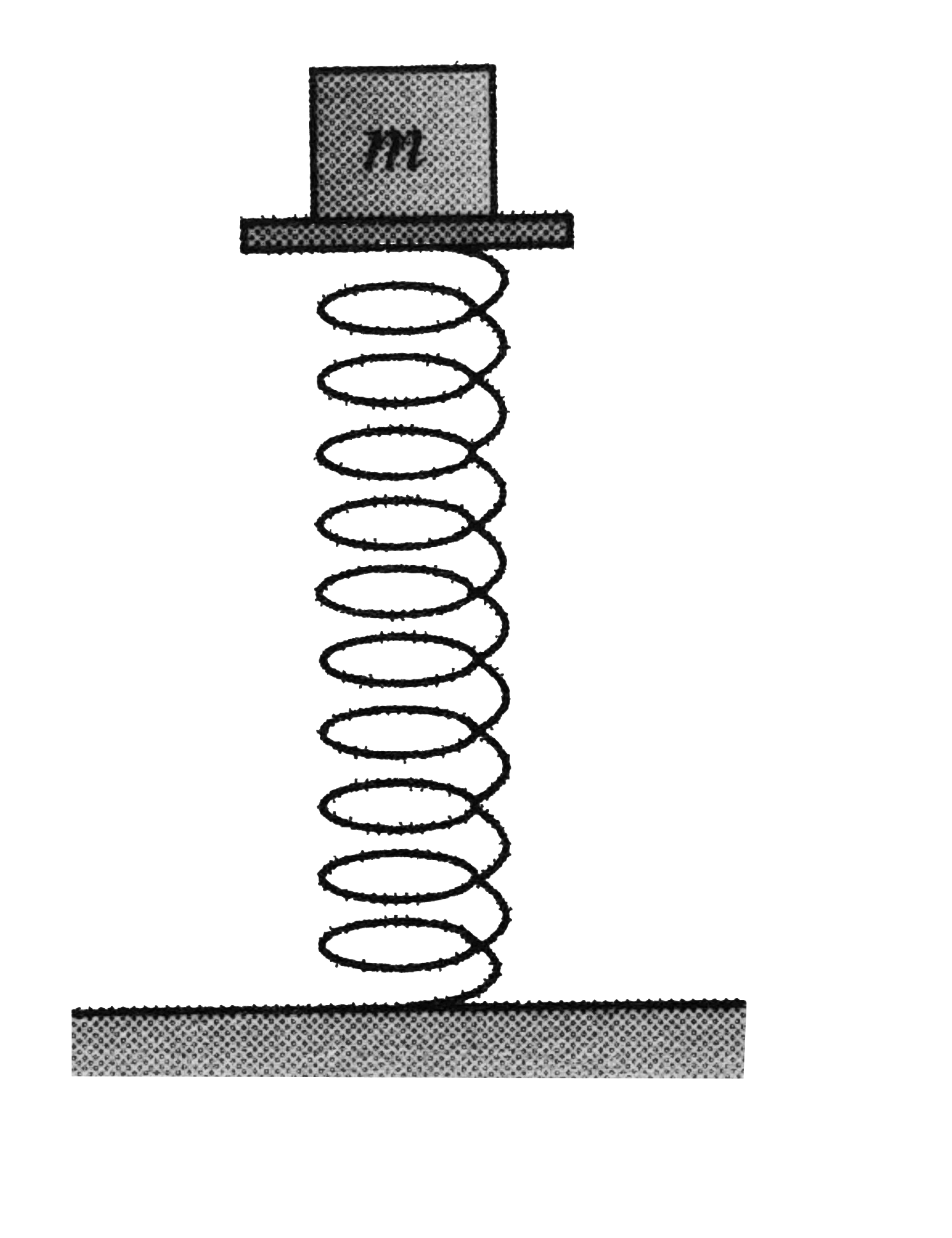
a. Find the acceleration of block just after release.
b. What is the compression in the spring at equilibrium.
c. What is the maximum compression in the spring.
d. Find the acceleration of block at maximum compression in the spring.
a. Just after release the spring is relaxed. Net force on the block is only its weight. Hence, acceleration of the block is g downward.
b. At equilibrium, net force on the block should be zero. Let x0 be the compression in the spring at equilibrium.
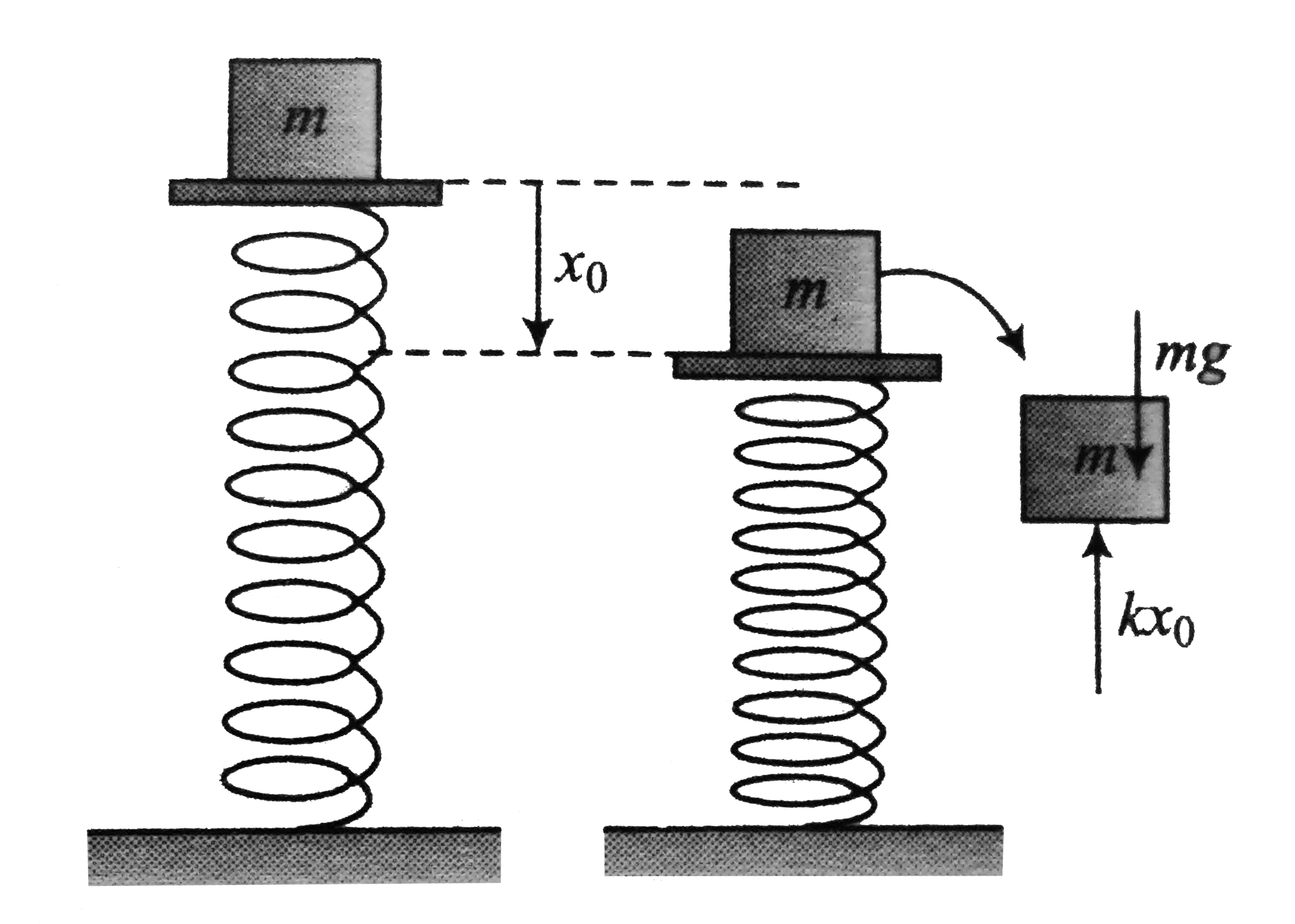
Applying Newton's second law,
mg=kx0 or x0=mgk
c. At maximum compression, the velocity of the block should be zero.
Let xmax be the maximum compression in the spring.
If we take block and spring as system, no external force and non-conservative force is doing work.

Applying mechanical energy conservation ΔK+ΔU=0
As the block is released from rest net charge and finally comes to rest. Hence, net change in its kinetic energy will be zero.
Net change in potential energy of the sytem
ΔU=ΔUgr+ΔUsp=(−mgxmax)+(12kx2max)=0
⇒0+(−mgxmax+12kx2max)=0 or xmax=2mgk
d. At maximum compression, writing equation of motion of block
kxmax−mg=ma where xmax=2mgk
Hence, acceleration of the block is g upward.
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Solved Examples
15 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.1
25 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
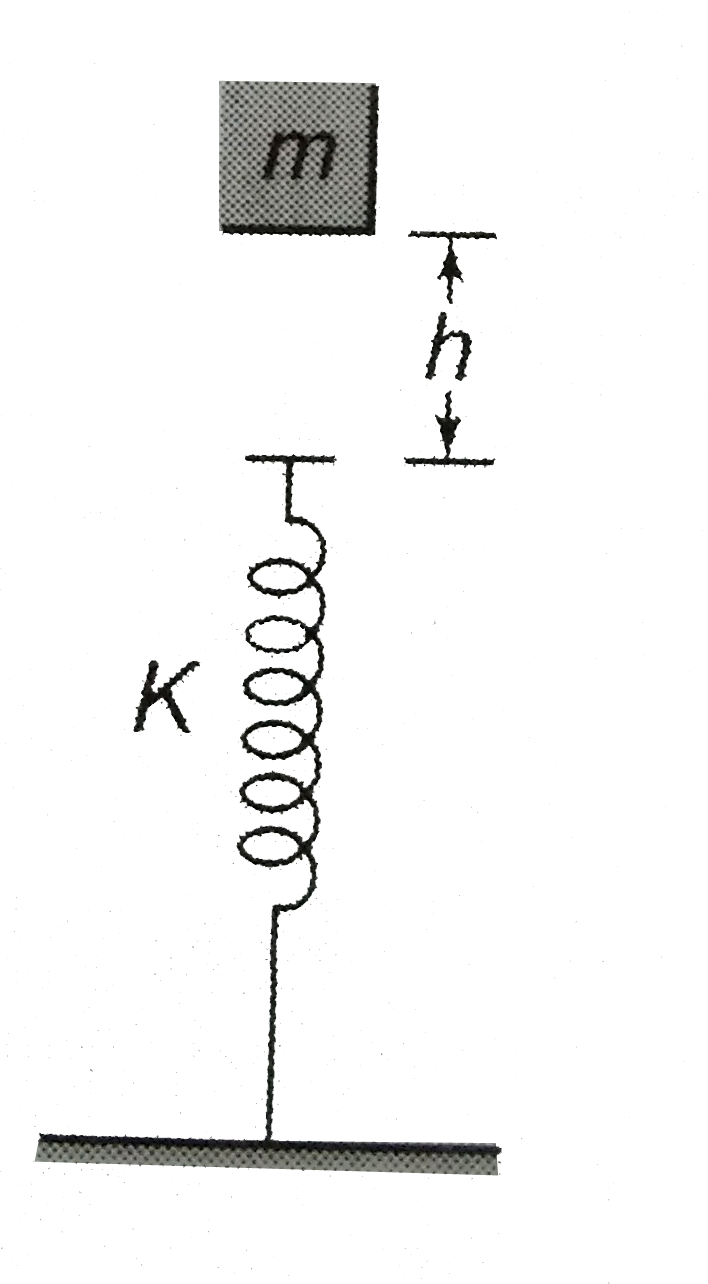
A block is released from height h, find the maximum compression of spring of spring constant k.
View SolutionA block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)
View Solution
Knowledge Check
Find maximum compression is the spring from the given figure.
 A√25mB16√25mC3√25mD6√25m
A√25mB16√25mC3√25mD6√25m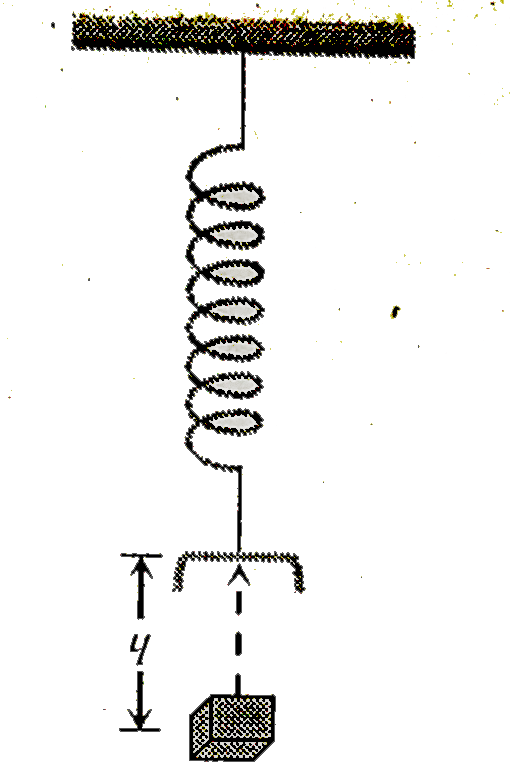
A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x thenAmgh=12kx2Bmg(h+x)=12kx2Cmgh=12k(x+h)2Dmg(h+x)=12k(x+h)2A slab S of mass m released from a height h0, from the top of a spring of force constant k. The maximum compression x of the spring is given by the equation.
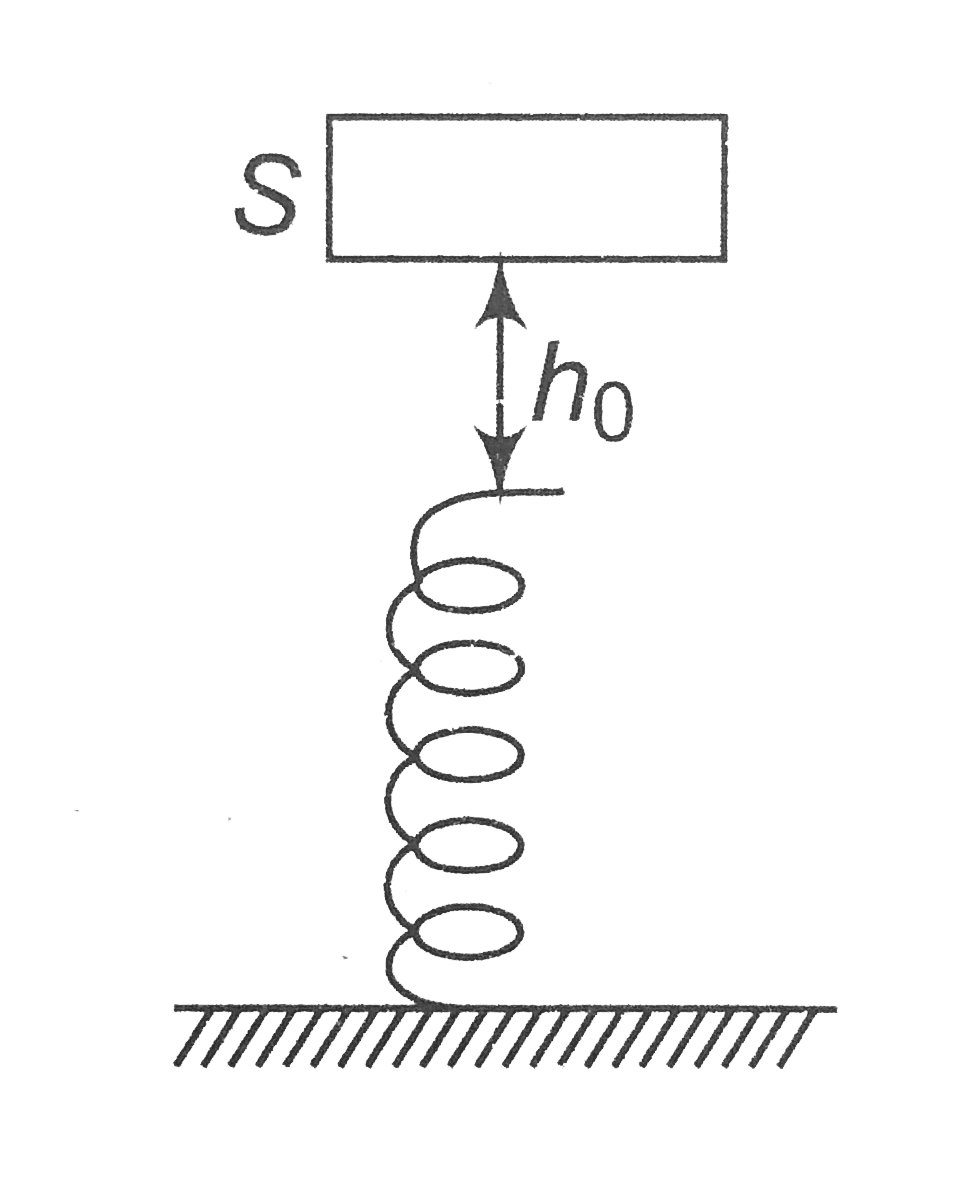 Amgh0=12kx2Bmg(h0−x)=12kx2Cmgh0=12k(h0+x)2Dmg(h0+x)=12kx2
Amgh0=12kx2Bmg(h0−x)=12kx2Cmgh0=12k(h0+x)2Dmg(h0+x)=12kx2
The block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionA block of mass m is released from rest onto a spring. A having stiffness kA=mg/2h as shown in figure. If the block compresses spring B through a distance h, find the:
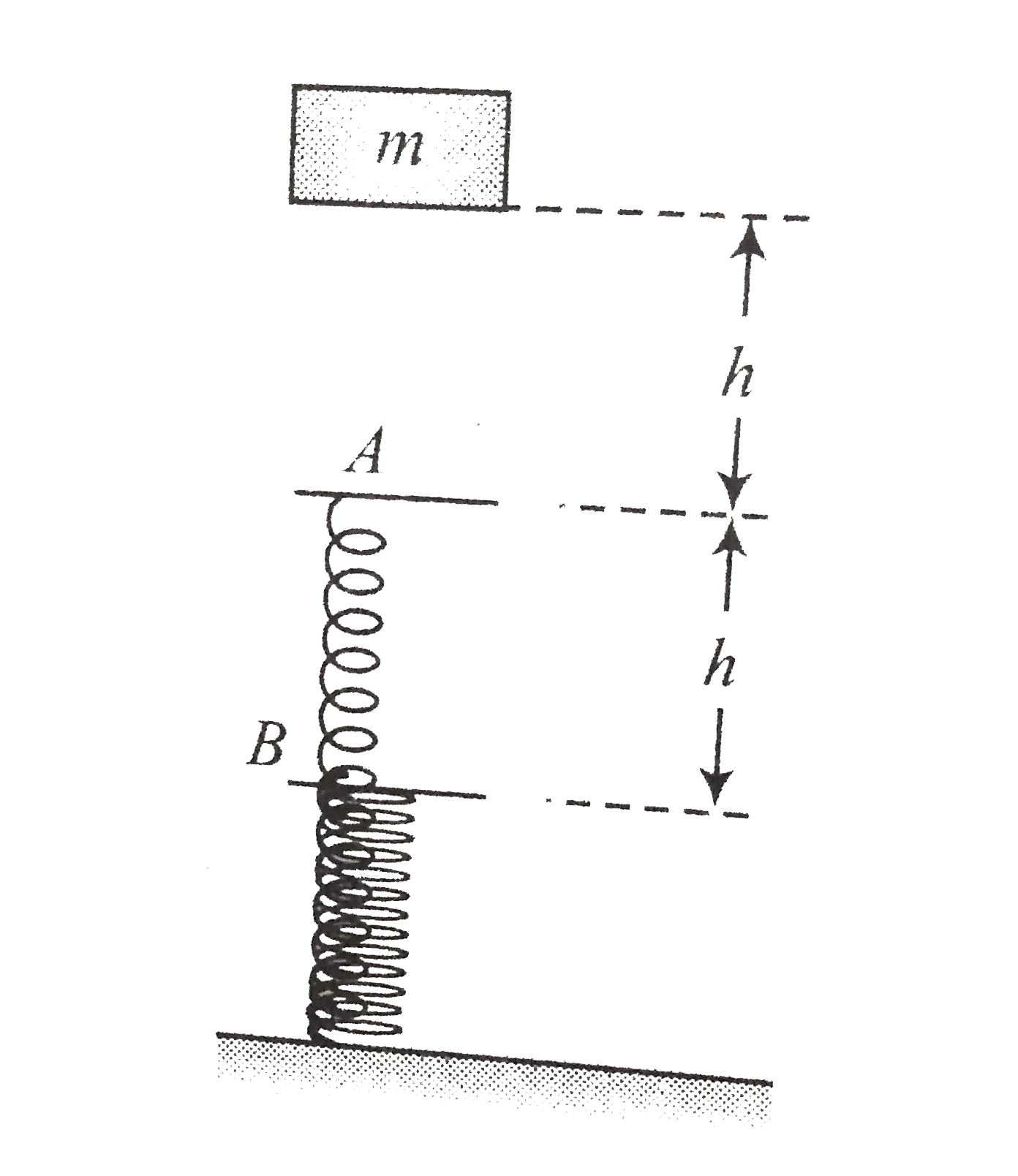
a. stiffness of the spring B
b. equilibrium position of the block
c. maximum velocity of the block
d. maximum acceleration of the block
View SolutionA block of mass m moving at a speed v0 compresses a spring of spring constant k as shown in the figure. Find (a) the maximum compression of spring and (b) speed of the block when the spring is compressed to half of maximum compression.
View SolutionA block of mass m strikes a light pan fitted with a vertical spring after falling through a distance h. If the stiffness of the spring is k, find the maximum compression of the spring.
View SolutionA block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

View Solution