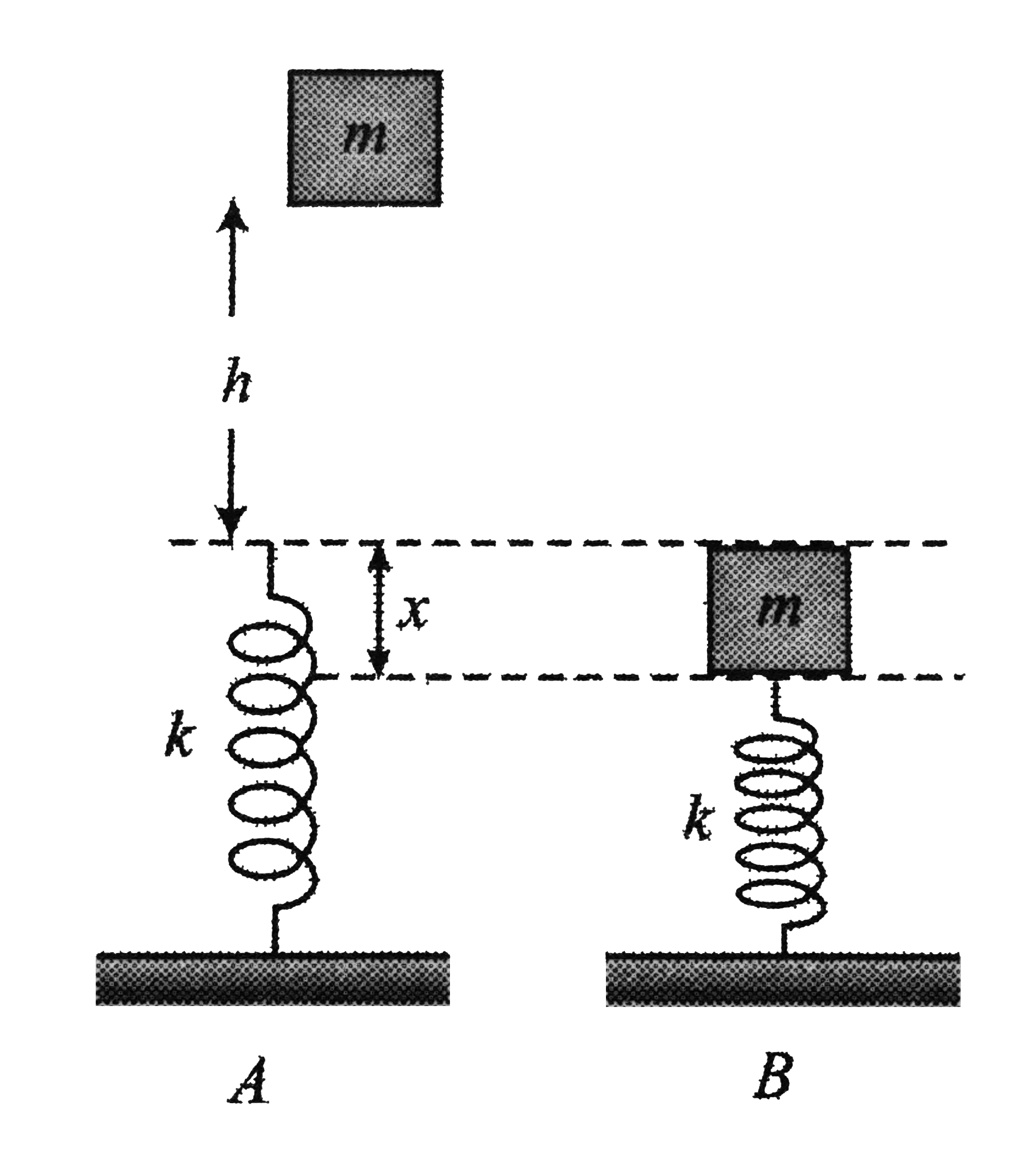
A block of mass $m$ is released from rest onto a spring. A having stiffness $k_{A} = m g / 2 h$ as shown in figure. If the block compresses spring B through a distance h, find the:

a. stiffness of the spring B
b. equilibrium position of the block
c. maximum velocity of the block
d. maximum acceleration of the block

Video Solution

Text Solution

Verified by Experts

The correct Answer is:a. $\frac{4 m g}{h}$ ; b. $\frac{h}{9}$ ; c. $\frac{4}{3} \sqrt{2 g h}$ ; d. $4 g ↑$

Updated on:21/07/2023

A block of mass m compresses a spring iof stifffness k through a distacne $l / 2$ as shown in the figure .If the block is not fixed to the spring the period of motion of the block is

A $2 π \sqrt{\frac{m}{k}}$
B $(π + 4) \sqrt{\frac{m}{k}}$
C $(1 + π) \sqrt{\frac{m}{k}}$
DNone of these
A block of mass m is attached to two unstretched springs of spring constants $k_{1} and k_{2}$ as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.

A $\sqrt{\frac{k_{1} + k_{2}}{m}} x$
B $\sqrt{\frac{k_{1} k_{2}}{m (k_{1} + k_{2})}} x$
C $\sqrt{\frac{k_{1}^{2} k_{2}^{2}}{m (k_{1}^{2} + k_{2}^{2})}} x$
D $\sqrt{\frac{k_{1}^{3} k_{2}^{3}}{m (k_{1}^{3} + k_{2}^{3})}}$
A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x then
A $m g h = \frac{1}{2} k x^{2}$
B $m g (h + x) = \frac{1}{2} k x^{2}$
C $m g h = \frac{1}{2} k {(x + h)}^{2}$
D $m g (h + x) = \frac{1}{2} k {(x + h)}^{2}$