A block of mass m sliding down an inclined at constant speed is initial at a height h shown the ground as shown in the figure above . The coefficient of kinetic friction between the mass and the inclined is μ . If the mass constinues to slide down the inclined at a constant speed how much energy is displaced by friction by the time the mass reaches the bottom of the incline?
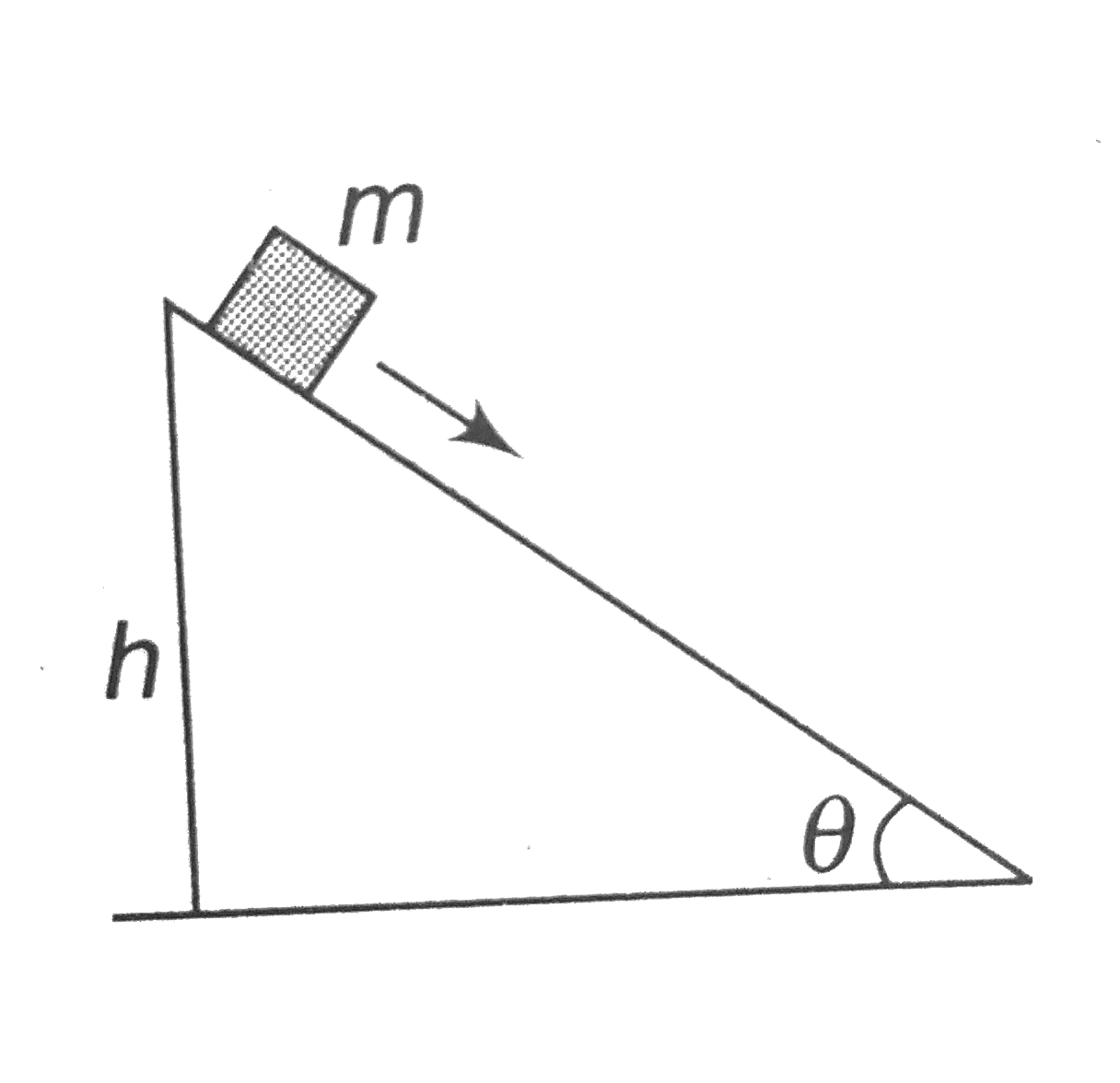
mgh/θ
mgh
μmgh/sinθ
mghsinθ
The correct Answer is:B
Taking block as system
Wf=ΔK+ΔU=0−mgh
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Mechanical Power
25 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Circular Motion In Vertical Plane
21 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Potential Energy, Conservative And Non-Conservative Forces
28 Videos
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test
30 Videos
Similar Questions
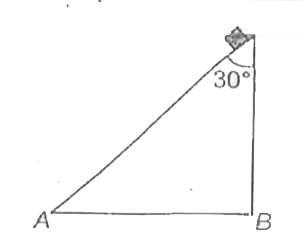
A body of mass M starts sliding down on the inclined plane where the critical angle is ∠ACB=30∘ as shown in figure. The coefficient of kinetic friction will be
View SolutionA block slides down a curved frictionless track and then up an inclined plane as in figure. The coefficient of kinetic friction between the block and incline is μk. Find the maximum height reached by the clock.

View Solution
Knowledge Check
A block of mass m is sliding down an inclined plane with constant speed. At a certain instant t0, its height above the ground is h. The coefficient of kinetic friction between the block and the plane is μ. If the block reaches the ground at a later instant tg, then the energy dissipated by friction in the time interval (tg−t0) is -
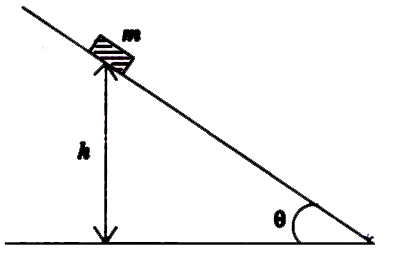 AμmghBμmgh/sinθCmghDμmgh/cosθ
AμmghBμmgh/sinθCmghDμmgh/cosθA block of mass m is placed on a rough inclined plane of inclination θ kept on the floor of the lift. The coefficient of friction between the block and the inclined plane is μ. With what acceleration will the block slide down the inclined plane when the lift falls freely ?
AZeroBgsinθ−μgcosθCgsinθ−μgcosθDNone of theseA block slides down a curved frictionless track and then up an inclined plane as in figure. The coefficient of kinetic friction between the block and incline is μk. Find the maximum height reached by the clock.
 Ah1+μcosθBh1+μtanθCh1+μcotθDhμtanθ
Ah1+μcosθBh1+μtanθCh1+μcotθDhμtanθ
A block sliding down on a rough 45∘ inclined planes has half the velocity it would have been, the inclined plane is smooth. The coefficient of sliding friction between the the block and the inclined plane is
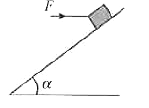
View SolutionA block of mass m in the equilib rium on a rough inclined plane with inclination α and coefficient of friction as shown in the figure (μ<tanα). A force F is applied on the block which makes an angle θ with the horizontal as shown in diagram.
View SolutionA block sliding down on a rough 45∘ inclined plane has half the velocity it would have been, the inclined plane is smooth. The coefficient of sliding friction between the block and the inclined plane is
View SolutionA block is placed on an inclined plane. The angle of inclination of the plane is such that the block slides down the plane at a constant speed. The coefficient of kinetic friction is
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View Solution
