A block is placed on an inclined plane. The angle of inclination of the plane is such that the block slides down the plane at a constant speed. The coefficient of kinetic friction is
To solve the problem of finding the coefficient of kinetic friction for a block sliding down an inclined plane at a constant speed, we can follow these steps:
1. Identify the Forces Acting on the Block:
When a block is placed on an inclined plane, the forces acting on it are:
- The gravitational force (weight) Mg acting vertically downwards.
- The normal force N acting perpendicular to the surface of the incline.
- The frictional force Ff acting opposite to the direction of motion (up the incline).
2. Resolve the Gravitational Force:
The weight Mg can be resolved into two components:
- Parallel to the incline: Mgsinθ
- Perpendicular to the incline: Mgcosθ
3. Set Up the Equation for Forces:
Since the block is sliding down at a constant speed, the net force acting on it is zero. Therefore, the force pulling the block down the incline (gravitational component) must be balanced by the frictional force:
Mgsinθ=Ff
4. Express the Frictional Force:
The frictional force can be expressed in terms of the normal force and the coefficient of kinetic friction μ:
Ff=μN
The normal force N is equal to the perpendicular component of the weight:
N=Mgcosθ
Thus, we can write:
Ff=μ(Mgcosθ)
5. Equate the Two Expressions for Frictional Force:
Setting the two expressions for the frictional force equal gives:
Mgsinθ=μ(Mgcosθ)
6. Simplify the Equation:
We can cancel Mg from both sides (assuming M≠0):
sinθ=μcosθ
7. Solve for the Coefficient of Kinetic Friction:
Rearranging the equation gives:
μ=sinθcosθ=tanθ
8. Conclusion:
Therefore, the coefficient of kinetic friction μ is:
μ=tanθ
Final Answer:
The coefficient of kinetic friction is μ=tanθ.
---
When a block is placed on an inclined plane, the forces acting on it are:
- The gravitational force (weight) Mg acting vertically downwards.
- The normal force N acting perpendicular to the surface of the incline.
- The frictional force Ff acting opposite to the direction of motion (up the incline).
The weight Mg can be resolved into two components:
- Parallel to the incline: Mgsinθ
- Perpendicular to the incline: Mgcosθ
Since the block is sliding down at a constant speed, the net force acting on it is zero. Therefore, the force pulling the block down the incline (gravitational component) must be balanced by the frictional force:
Mgsinθ=Ff
The frictional force can be expressed in terms of the normal force and the coefficient of kinetic friction μ:
Ff=μN
The normal force N is equal to the perpendicular component of the weight:
N=Mgcosθ
Thus, we can write:
Ff=μ(Mgcosθ)
Setting the two expressions for the frictional force equal gives:
Mgsinθ=μ(Mgcosθ)
We can cancel Mg from both sides (assuming M≠0):
sinθ=μcosθ
Rearranging the equation gives:
μ=sinθcosθ=tanθ
Therefore, the coefficient of kinetic friction μ is:
μ=tanθ
The coefficient of kinetic friction is μ=tanθ.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - CONSOLIDATED EXERCISE.1videos
FRICTION
- BOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - CONSOLIDATED EXERCISE. (MULTIPAL-CHOICE QUESTION WITH ONE OR MORE THAN ONE CORRECT ANSWER)3videos
FRICTION
- BOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES (Read the given statements and select the correct option.)1videos
FRICTION
- BOOK - CENGAGE PHYSICSCHAPTER - ELASTICITYEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES10videos
ELASTICITY
- BOOK - CENGAGE PHYSICSCHAPTER - SOUNDEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISE10videos
SOUND
Similar Questions
A body freely released from A slides down a smooth inclined plane 'AB' and then a rough incline plane 'BC' such that BC = N (AB). If the block comes to rest at C, then coefficient of kinetic friction between the block and inclined plane is?
View SolutionA block is placed on the top of a plane inclined at 37∘ with horizontal. The length of the plane is 5m. The block slides down the plane and reaches the bottom.
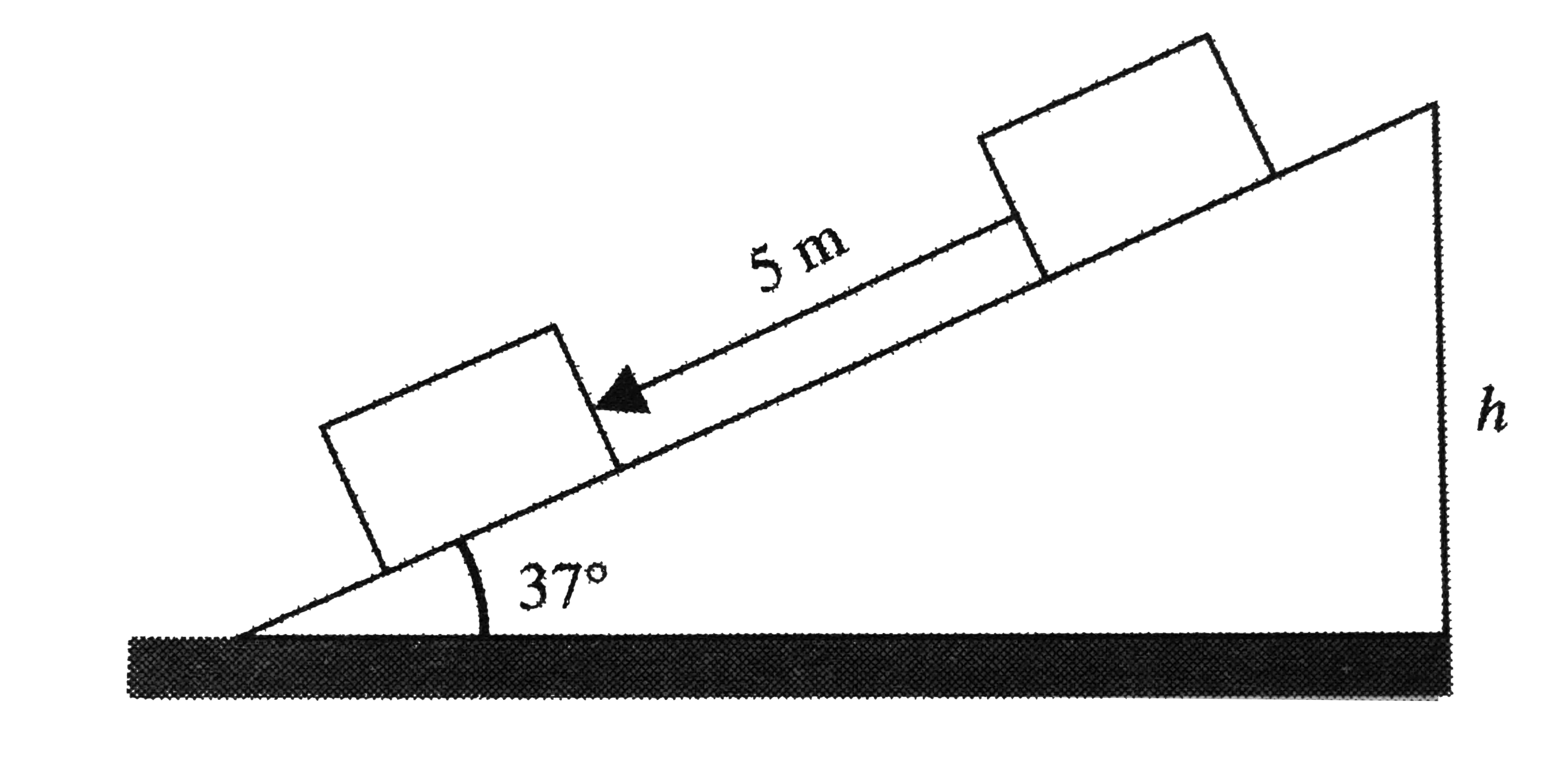
a. Find the speed of the block at the bottom if the inclined plane is smooth.
b. Find the speed of the block at the bottom if the coefficient of friction is 0.25.View Solution
Knowledge Check
- Question 1 - Select One
A block has been placed on an inclined plane . The slope angle of θ of the plane is such that the block slides down the plane at a constant speed . The coefficient of kinetic friction is equal to :
Asin θBcos θCgDtan θ - Question 2 - Select One
A block has been placed on an inclined plane with the slope angle θ. Block slide down the plane at constant speed. The cofficient of Kinetic friction is equal to
AsinθBcosθCgDtanθ - Question 3 - Select One
A block of mass m is placed on a rough inclined plane. When the inclination of the plane is θ , the block just beging to slide down the plane under its own weight. The minimum force applied parallel to the plane, to move the block up the plane, is.
AmgsinθB2mgsinθCmgcosθDmgtanθ
A block slides down on inclined plane (angle of inclination 60∘ ) with an accelration g/2 Find the coefficient friction
 View Solution
View SolutionA block of mass 10 kg is placed on an inclined plane when the angle of inclination is 30∘. The block just begins to slide down the plane. The force of static friction is
View SolutionA block of mass 5 kg is placed on a rough inclined plane. The inclination of the plane is gradually increased till the block just begins to slide down. The inclination of the plane is than 3 in 5. The coefficient of friction between the block and the plane is (Take, g=10m/s2)
View SolutionA block of 150kg is placed on an inclined plane withh an angle of 60∘. Calculate of the weight parallel to the inclined plane.
 View Solution
View SolutionWhat is the time required for a block to slide down from the top to the bottom ofan inclined plane 6.4 m long if the inclination of the plane with the horizonta l is 30° and the coefficient of friction= 0.2?
View Solution

