A block of mass M1 and a block of mass M2 are connected by a string that passes over a pulley as shown in Fig. The pulley is a uniform disk of radius R and mass M. Find the acceleration of the two object, using the concepts of angular momentum and torque.
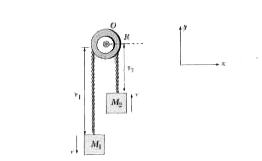
(1) If the block M1 moves upward, the block M2 moves downward, and the pulley will rotate counterclockwise. This problem is same as Sample Problem we have already solved, except that now we have to use angular momentum and torque to find acceleration.
(2) We define the blocks and pulley as our system. We consider the axle of the pulley as our axis. We can write the angular momentum of the system considering the ball and the block that are moving translationally and the pulley which is undergoing pure rotation. The external torque on the system about the axis is due to the weights of the blocks.
Calculations: Due to constraint, the blocks have same speed n. We can find angular momentum using the definition of angular momentum about the axle, given by equation →L=→r×→p.
The momentum and position vectors are given by
→P1=−M1νˆjandr1=−Rˆi−y1ˆj
Using →L=→r×→p, the angular momentum of block 1 is M1νRˆk.
Similarly, for block 2, momentum and position vectors are given by
→P2=+M2νˆjandr1=Rˆi+y2ˆj
Using →L=→r×→p, the angular momentum of block 2 is M2νRˆk about our chosen axis.
The angular momentum of the pulley can be found using L=Iω. It is given by MpR2ωˆk/2 about our chosen axis.
We calculate the external torque acting on the system about the pulley axle. The force is being exerted by the axle on the pulley, but it does not produce torque about the axle as the length of moment arm is zero.
The gravitational force M1→g acting on block 1 produces a torque about the axle equal to M1gRˆk and the gravitational force M2→g acting on block 2 produces a torque about the axle equal in magnitude to −M2gRˆk, where R is the moment arm of the force about the axle. Thus, the total external torque about the pulley axle is
∑τext=M1gRˆk−M2gRˆk
Writing an expression for the total angular momentum of the system,
L=(M1νR+M2νR+MνR)ˆk
Substituting this expression and the total external torque in
∑text=dLdt
M1gRˆk−M2gRˆk=ddt[(M1+M2+M)νR]ˆk
M1gR−M2gR=(M1+M2+M)Rdνdt
Recognizing that dν/dt=a and solving Eq. for a
a=(M1−M2)gM1+M2+M
Topper's Solved these Questions
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - CHECKPOINT
18 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PROBLEMS
100 Videos
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)
2 Videos
Similar Questions
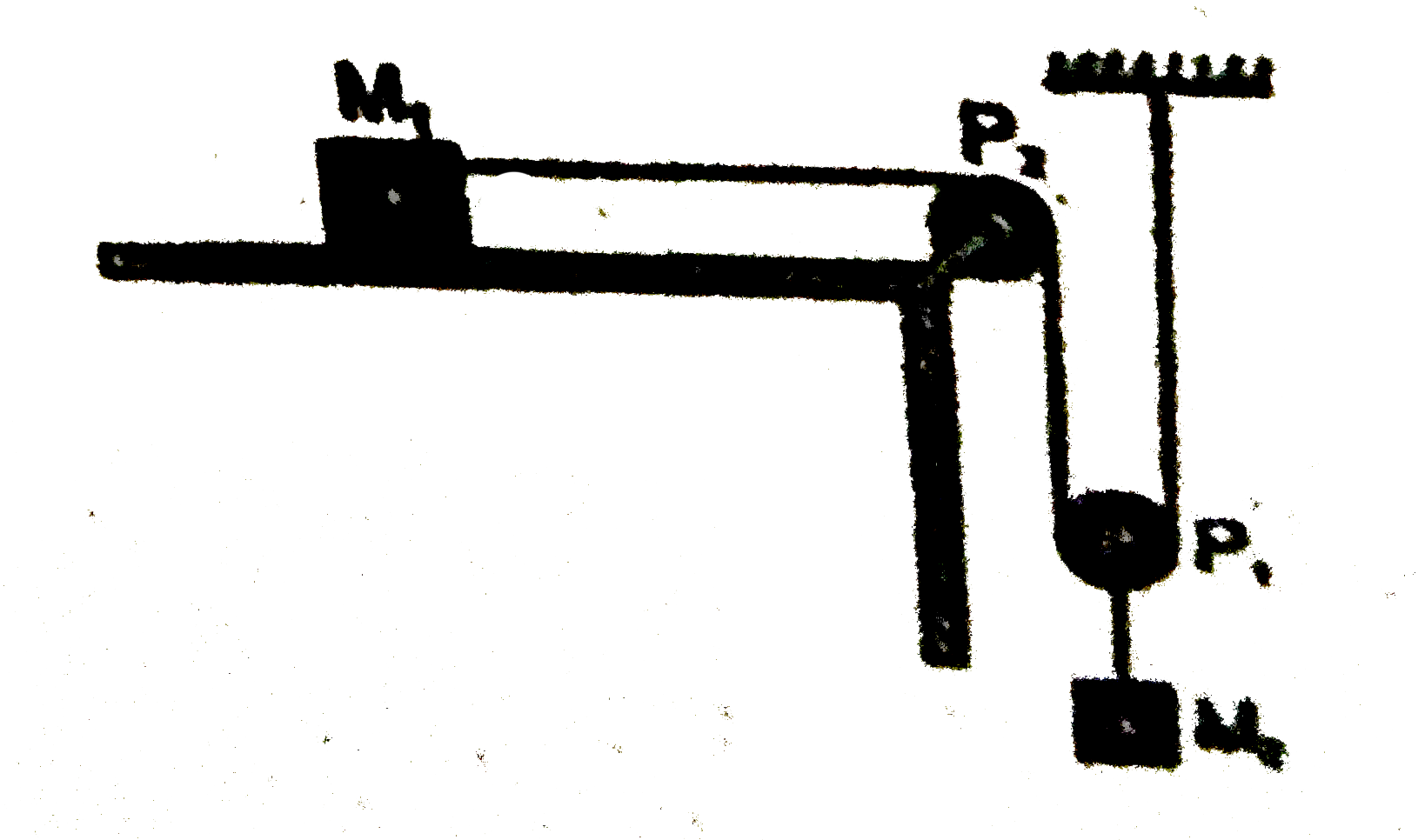
Blocks of mass M1 and M2 are connected by a cord which passes over the pulleys P1 and P2 as shown in the figure. If there is no friction, the acceleration of the block of mass M2 will be
View SolutionTwo bodies of masses m1 and m2 are connected a light string which passes over a frictionless massless pulley. If the pulley is moving upward with uniform acceleration g2, then tension in the string will be
View Solution
Knowledge Check
Blocks of mass M1 and M2 are connected by a cord which passes over the pulleys P1 and P2 as shown in the figure. If there is no friction, the acceleration of the block of mass M2 will be
 AM2g(4M1+M2)B2M2g(4M1+M2)C2M1g(M1+4M2)D2M1g(M1+M2)
AM2g(4M1+M2)B2M2g(4M1+M2)C2M1g(M1+4M2)D2M1g(M1+M2)Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
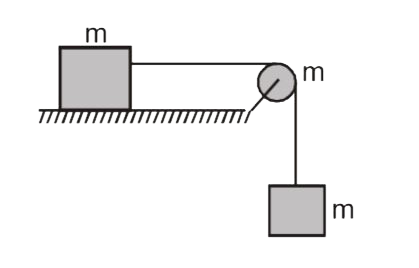
Figure shows two blocks of mass m and m connected by a string passing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley (uniform disc) has mass m and it can freely rotate about this axis. Find the acceleration of the mass m assuming that the string does not slip on the pulley.
View SolutionTwo masses m1andm2 are connected to the end of a string passing over a smooth pulley . The magnitude of tension in the string is T and the masses are moving with magnitude of acceleration a . If the masses are interchanged , then
View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionTwo bodies of masses m1 and m2 are connected a light string which passes over a frictionless massless pulley. If the pulley is moving upward with uniform acceleration g2, then tension in the string will be
View SolutionTwo masses m1andm2 are connected to the end of a string passing over a smooth pulley . The magnitude of tension in the string is T and the masses are moving with magnitude of acceleration a . If the masses are interchanged , then
View Solution
