Two masses m1andm2 are connected to the end of a string passing over a smooth pulley . The magnitude of tension in the string is T and the masses are moving with magnitude of acceleration a . If the masses are interchanged , then
Both a and T will change
a will change but T will remain unchanged
T will change but a will remain unchanged
None of these will change
The correct Answer is:D
To solve the problem of two masses m1 and m2 connected by a string over a smooth pulley, we need to analyze the forces acting on each mass and derive expressions for tension and acceleration. Let’s go through the solution step by step.
Step 1: Identify the Forces
- For mass m1 (which is moving upwards), the forces acting on it are:
- Weight: m1g (downward)
- Tension: T (upward)
- For mass m2 (which is moving downwards), the forces acting on it are:
- Weight: m2g (downward)
- Tension: T (upward)
Step 2: Write the Equations of Motion
For mass m1:
T−m1g=m1a(1)
For mass m2:
m2g−T=m2a(2)
Step 3: Solve the Equations
Now, we can add equations (1) and (2) to eliminate T:
(T−m1g)+(m2g−T)=m1a+m2a
This simplifies to:
m2g−m1g=(m1+m2)a
Rearranging gives:
(m2−m1)g=(m1+m2)a
Thus, the acceleration a can be expressed as:
a=(m2−m1)g(m1+m2)(3)
Step 4: Find the Tension
Now, we can substitute a back into either equation (1) or (2) to find the tension T. Using equation (1):
T=m1g+m1a
Substituting a from equation (3):
T=m1g+m1((m2−m1)g(m1+m2))
This simplifies to:
T=m1g(1+(m2−m1)(m1+m2))
Combining terms:
T=m1g(m1+m2+m2−m1)(m1+m2)=m1m2g(m1+m2)(4)
Step 5: Interchanging the Masses
When the masses are interchanged, m1 becomes m2 and m2 becomes m1. The new acceleration a′ will be:
a′=(m1−m2)g(m1+m2)(5)
The tension T′ will also be:
T′=m2m1g(m1+m2)(6)
Conclusion
From equations (4) and (6), we see that the tension T remains the same regardless of the interchange of masses. The magnitude of acceleration changes direction but not magnitude.
Final Answer
- The magnitude of tension T does not change.
- The magnitude of acceleration a remains the same, but its direction reverses.
- For mass m1 (which is moving upwards), the forces acting on it are:
- Weight: m1g (downward)
- Tension: T (upward)
- Weight: m2g (downward)
- Tension: T (upward)
For mass m1:
T−m1g=m1a(1)
m2g−T=m2a(2)
Now, we can add equations (1) and (2) to eliminate T:
(T−m1g)+(m2g−T)=m1a+m2a
This simplifies to:
m2g−m1g=(m1+m2)a
Rearranging gives:
(m2−m1)g=(m1+m2)a
Thus, the acceleration a can be expressed as:
a=(m2−m1)g(m1+m2)(3)
Now, we can substitute a back into either equation (1) or (2) to find the tension T. Using equation (1):
T=m1g+m1a
Substituting a from equation (3):
T=m1g+m1((m2−m1)g(m1+m2))
This simplifies to:
T=m1g(1+(m2−m1)(m1+m2))
Combining terms:
T=m1g(m1+m2+m2−m1)(m1+m2)=m1m2g(m1+m2)(4)
When the masses are interchanged, m1 becomes m2 and m2 becomes m1. The new acceleration a′ will be:
a′=(m1−m2)g(m1+m2)(5)
The tension T′ will also be:
T′=m2m1g(m1+m2)(6)
From equations (4) and (6), we see that the tension T remains the same regardless of the interchange of masses. The magnitude of acceleration changes direction but not magnitude.
- The magnitude of tension T does not change.
- The magnitude of acceleration a remains the same, but its direction reverses.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -B) objective type questions (one option is correct)
59 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -C) objective type questions (More than one options are correct)
21 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - TRY YOURSELF
69 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
Knowledge Check
Two masses 8 kg and 12 kg are connected at the two ends of a light in extensible string that passes over a friction less pulley Find the acceleration of the masses and tension in the string , when the masses are released
 . Ag4Bg5Cg8Dg6
. Ag4Bg5Cg8Dg6
Two masses m and M(>m) are joined by a light string passing over a smooth light pulley. The centre of mass of the system moves with an acceleration

View SolutionTwo weights w1 and w2 are suspended from the ends of a light string passing over a smooth fixed pulley. If the pulley is pulled up at an acceleration g , the tension in the string will be
View SolutionTwo masses of 10 kg and 20 kg are connected with an inextensible string passing over two smooth pulleys as shown in the figure. The acceleration of 20 kg mass will be :
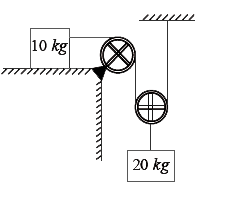
View SolutionTwo particles of masses m and M(M>m) are connected by a cord that passes over a massless, frictionless pulley. The tension T in the string and the acceleration a of the particles is
View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionTwo masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.
View SolutionTwo masses 8 kg and 12 kg are connected at the two ends of a light in extensible string that passes over a friction less pulley. Find the acceleration of the masses and tension in the string , when the masses are released
 .
.
View Solution

_PHY_E05_245_Q01.png)
