A block of mass m1 is kept on a fixed inclined plane and attached to a block of mass m2 by a rope as shown in Fig. 6-14a. The incline makes angle θ with horizontal and coefficient of friction is μ. Find range of m2 for which m1 remains at rest (given θ>tan−1μs).

Figure 6-14 (a) A block of mass m1 is kept on a fixed rough inclined plane and attached to a block of mass m2 by a rope.
This problem is about finding range. If we make m2 very light such that m2 becomes zero, m1 will tend to go down the inclined plane hence friction will act in upward direction. On the other hand, if we make m2 very heavy then m1 will definitely move up with the friction acting downward.
(2) It involves static friction as it is given in the sample problem that m1 remains at rest and also m1 at rest implies that m2 must be at rest. Also, from above discussion it is clear that static friction is going to change direction. So, we need to solve this problem in two parts.
(a) To find minimum value, assuming block m1 is in impending state to go down the inclined plane.
Calculation: If m2 is small then m, will tend to go down the incline for the smallest possible value of m2 for equilibrium m1 will experience maximum friction upward. Make free-body diagram as shown in Fig. 6-14b. For equilibrium of m2

For equilibrium of m1 along incline
T+μsFN−m1gsinθ=0
and perpendicular to incline
m1gcosθ−FN=0
Solving, we get
m2=m1(sinθ−μscosθ)
To find maximum value, assuming block m1 is in impending state to go up the inclined plane.
Calculation: Now if m2 is increased, friction on m1 will decrease as tension is increasing, but if we keep on increasing m2 then friction will become directed down the incline and for maximum value of m1 it will be directed downward and equal to fs,maxbecause m1 is about to move up. Make free-body diagram as shown in Fig 6-14c.

For equilibrium of m2
T=m2g
For equilibrium of m1 along incline
T−μsFN−m1gsinθ=0
and perpendicular to incline
m1gcosθ−FN=0
Solving above equation
m2=m1(sinθ+μscosθ)
Learn: As expected we are getting two different values of m2 for two different impending states of motion of m1.
In Case of: m2=m1sinθ, find value of friction force acting on m1.
Friction force is not required as T = mg balances m2 and T=m1gsinθ balances m1. At this value of m1 friction shifts the direction, hence it is zero at this value. If we have mass m2 lower than this, m1 tends to go down with friction acting up the incline and vice versa.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - CHECKPOINTS5videos
FORCE AND MOTION-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PROBLEMS33videos
FORCE AND MOTION-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
FORCE AND MOTION - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)3videos
GAUSS' LAW
Similar Questions
A block of mass m is kept on an inclined plane is angle inclination θ(<ϕ), where ϕ= angle of friction. Then :
 View Solution
View SolutionA block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
View Solution
Knowledge Check
- Question 1 - Select One or More
A block of mass m in the equilib rium on a rough inclined plane with inclination α and coefficient of friction as shown in the figure (μ<tanα). A force F is applied on the block which makes an angle θ with the horizontal as shown in diagram.
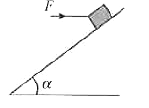 ANormal force on the block mgcosα+Fsinθ.BMinimum force f to keep the blockin equilibrium Fmin=mg(sinα−μcosα)2μ√1+μ2Cμ=tanθDNone of these
ANormal force on the block mgcosα+Fsinθ.BMinimum force f to keep the blockin equilibrium Fmin=mg(sinα−μcosα)2μ√1+μ2Cμ=tanθDNone of these - Question 2 - Select One
A block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
AmgcosθB√μ2+1mgcosθCμmgcosθ√μ2+1Dμmgθ - Question 3 - Select One
A block of mass mm remains stationary on a fixed inclined plane of inclination θ . If μ= coefficient of static friction the reaction of ground on the block is:
AμgcosθBmgcosθCmgsinθDmg↓
A cubical block of mass m is sliding on an inclined right angle trough as shown in the figure. If coefficient of friction is μ , find the acceleration of the block.
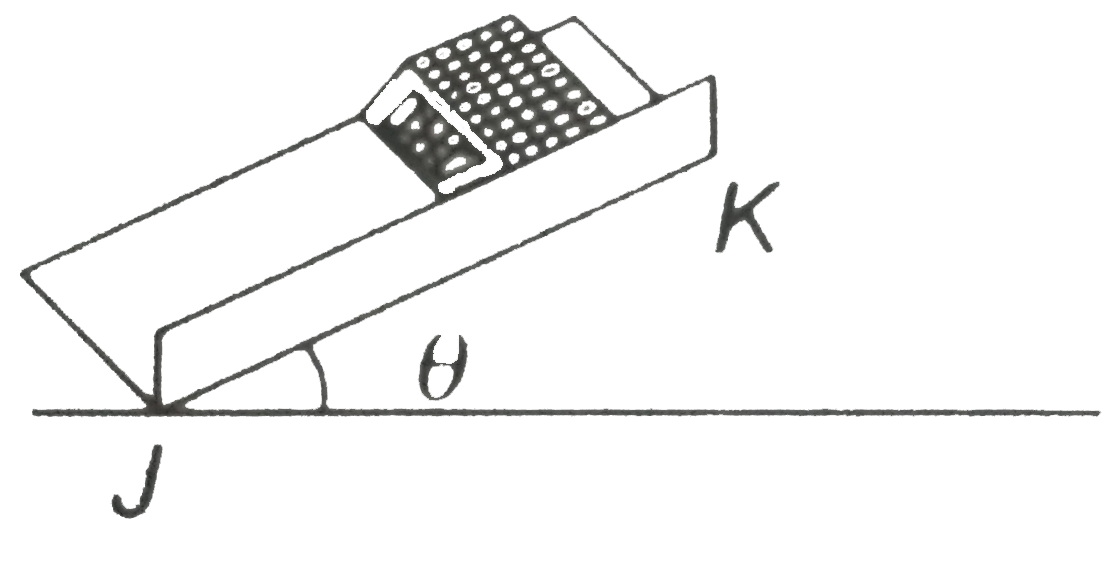 View Solution
View SolutionA block of mass 10 kg is kept on a fixed rough (μ=0.8) inclined plane of angle of inclination 30∘. The frictional force acting on the block is
 View Solution
View SolutionA block of mass 10 kg is kept on a fixed rough (μ=0.8) inclined plane of angle of inclination 30∘. The frictional force acting on the block is
 View Solution
View SolutionA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View SolutionA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View Solution

