A block of mass m1=3.70 kg on a frictionless plane inclined at angle 30.0∘ is connected by a cord over a massless, frictionless pulley to a second block of mass m2=2.30 kg (see Fig. 5-32).
(a) What is the magnitude of the acceleration of each block?
(b) What is the direction of the acceleration of the hanging block ?
(c) What is the tension in the cord?
The free-body diagram for each block is shown in Fig. 5-33. T is the tension in the cord and θ=30∘ is the angle of the incline. For block 1, we take the +x direction to be up the incline and the +y direction to be in the direction

Figure 5-32 Block on frictionless inclined plane connected by a cord over a pulley to another block.
of the normal force →FN that the plane exerts on the block. For block 2, we take the +y direction to be down.
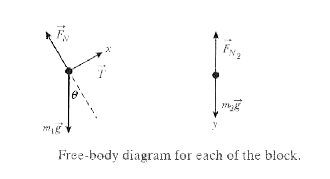
Figure 5-33 Free-body diagram for each of the block.
In this way, the accelerations of the two blocks can be represented by the same symbol a, without ambiguity Applying Newton.s second law to the x and y axes for block 1 and to the y axis of block 2, we obtain
T−m1gsinθ=m1a (5−41)
FN−m1gcosθ=0 (5−42)
m2g−T=m2a (5−43)
respectively. The first and third of these equations provide a simultaneous set for obtaining values of a and T. The second equation is not needed in this problem, since the normal force is neither asked for nor is it needed as part of some further computation (such as can occur in formulas for friction).
Calculation:: We add Eqs. (5-41) and (5-43) above:
m2g−m1gsinθ=m1a+m2a.
Consequently, we find
a=(m2−m1sinθ)gm1+m2
=[2.30 kg−(3.70 kg)sin30.0∘](9.80 m/s2)3.70 kg+2.30 kg
=0.735 m/s2
(b) What is the direction of the acceleration of the hanging block ?
Reasoning: The result for a is positive, indicating that the acceleration of block 1 is indeed up the incline and that the acceleration of block 2 is vertically down.
( c ) What is the tension in the cord?
Calculation: The tension in the cord is
T=m1a+m1gsinθ
=(3.70 kg)(0.735 m/s2)+(3.70 kg)(9.80 m/s2)sin30.0∘
=20.8 N.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - CHECKPOINT5videos
FORCE AND MOTION - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PROBLEMS52videos
FORCE AND MOTION - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (Integer Type )5videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)1videos
FORCE AND MOTION-II
Similar Questions
A block of mass M1=3kg on a smooth fixed inclined plane of angle 30∘ is connected by a cord over a small frictionless pulley to a second block mass 2kg hanging vertically. The tension in the cord and the acceleration of each block are ………............. and ...................... respectively.
 View Solution
View SolutionFigure 5-59 shows a box of mass m2=1.0 kg on a friction-less plane inclined at angle θ=30∘. It is connected by a cord of negligible mass to a mass m1=2.5 kg on a horizontal frictionless surface. The pulley is frictionless and massless. (a) If the magnitude of horizontal force →F is 2.3 N, what is the tension in the connecting cord? (b) What is the largest value the magnitude of →F may have without the cord becoming slack?
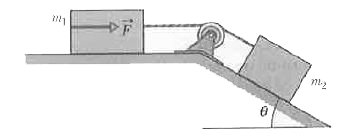 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass 3kg which is on a smooth inclined plane making an angie of 30∘ to the horizontal is connected by cord passing over light frictionless pulley to second block of mass 2kg hanging vertically. What is the acceleration of each block and what is the tension of the cord ?
A0.98m/s2,17.6NB1.98m/s2,19.6NC0.49m/s2,9.8ND1.47m/s2,4.9N - Question 2 - Select One
A block of mass 3kg which is on a smooth inclined plane making angie of 30∘ to the horizontal is connected by cord passing over light frictionless pulley to second block of mass 2kg hanging vertically. What is the acceleration of each block and waht is the tension of the cord ? .
A0.98m/s2,17.6NB1.98m/s2,19.6NC0.49m/s2,9.8ND1.47m/s2,4.9N - Question 3 - Select One
Two particles of masses m and M(M>m) are connected by a cord that passes over a massless, frictionless pulley. The tension T in the string and the acceleration a of the particles is
AT=2mM(M−m)g,aMm(M+m)gBT=2mM(M+m)g,a=(M−mM+m)gCT=(M−mM+m)g,a=(2mM(M+m))gDT=(Mm(M+m)g,a=(2mM(M+m))g
A horizontal force of 4 N is applied to a block of mass 2 kg resting on a frictionless table. What is the acceleration of the block in ms−2 ?
View SolutionA block of mass m1=2kg on a smooth inclined planeat angle 30∘ is connected to a second block of mass m2=3kg by a cord passing over a frictionless pulley as shown in figure. The acceleration of each block is - (Assume g=10m/sec2 )
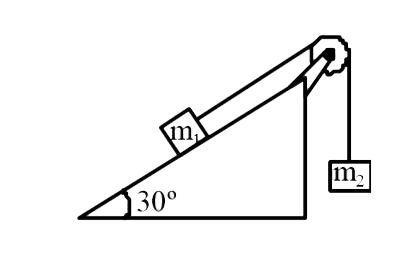 View Solution
View SolutionTwo blocks are connected by a cord passing over a small frictionless pulley and resting on frictionless planes as shown in the figure. The acceleration of the blocks is :
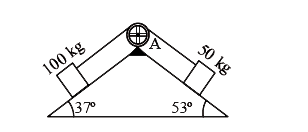 View Solution
View SolutionA block of mass 5 kg resting on a horizontal surface is connected by a cord, passing over a light frictionless pulley to a hanging block of mass 5 kg. The coefficient of kinetic friction between the block and the surface is 0.5. Tension in the cord is (g=9.8m/s2 )
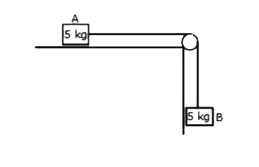 View Solution
View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View Solution

