A block of mass 5 kg resting on a horizontal surface is connected by a cord, passing over a light frictionless pulley to a hanging block of mass 5 kg. The coefficient of kinetic friction between the block and the surface is 0.5. Tension in the cord is (g=9.8m/s2 )
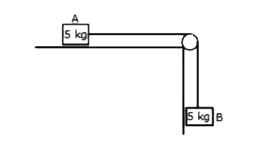
49 N
Zero
36.75 N
12.75N
The correct Answer is:C
Step by step video & image solution for A block of mass 5 kg resting on a horizontal surface is connected by a cord, passing over a light frictionless pulley to a hanging block of mass 5 kg. The coefficient of kinetic friction between the block and the surface is 0.5. Tension in the cord is ( g =9.8m//s^(2) ) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- NLM & FRICTIONBOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - EXERCISE-2
66 Videos
- NLM & FRICTIONBOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - EXERCISE-2(Level-II)
25 Videos
- NLM & FRICTIONBOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - SOLVED EXAMPLE
16 Videos
- NEWTON'S LAWS OF MOTION & FRICTION BOOK - MOTIONCHAPTER - NEWTON'S LAWS OF MOTION & FRICTION EXERCISE - Exercise - 3 Section-B
12 Videos
- ONE DIMENSION MOTIONBOOK - MOTIONCHAPTER - ONE DIMENSION MOTIONEXERCISE - Exercise - 3 |Section - B Previous Year Problems | JEE MAIN
12 Videos
Similar Questions
Two blocks A and B of respective masses 6 kg and 4 kg are connected with a string passing over a light friction less pulley as shown in the figure . The coefficient of friction between the block A and horizontal surface is 0.4 . Then the minimum mass of block C which should be placed over A to prevent it from moving is :
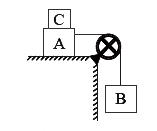
View SolutionA block of mass 8 kg is sliding on a surface inclined at an angle of 45∘ with the horizontal . Calculate the acceleration of the block . The coefficient of friction between the block and surface is 0⋅6 ( Take g = 10m/s2)
View Solution
Knowledge Check
A block of mass 5 kg resting on a horizontal surface is connected by a cord, passing over a light frictionless pulley to a hanging block of mass 5 kg. The coefficient of kinetic friction between the block and surface is 0.5. Tension in the cord is (take, g=9.8ms−2)
 A49 NBzeroC36.75 ND12.75 N
A49 NBzeroC36.75 ND12.75 NA block A of mass m1 rests on a horizontal table. A light string connected to it passes over a frictionless pully at the edge of the table and from its other end another block B of mass m2 is suspended. The coefficient of kinetic friction between the block and the table is H. When the block A is sliding on the table, the tension in the string is
Am1m2(1+μk)g(m1+m2)Bm1m2(1−μk)g(m1)+m2C(m2+μkm1)g(m1+m2)D(m2−μkm1)g(m1+m2)A block of mass m is stationary on a horizontal surface. It is connected with a string which has no tension. The coefficient of friction between the block and surface is m . Then , the frictional force between the block and surface is:
 AzeroBμmgCμmgμDNone of these
AzeroBμmgCμmgμDNone of these
A block of mass 8 kg is sliding on a surface inclined at an angle of 45∘ with the horizontal. Calculate the acceleration of the block. The coefficient of friction between the block and surface is 0.6. (Take g=10m/s2)
View SolutionA block of mass m = 2kg is accelerating by a force F = 20N applied on a smooth light pulley as shown in the figure. If the coefficient of kinetic friction between the block and the surface is μ=0.3, find its acceleration.
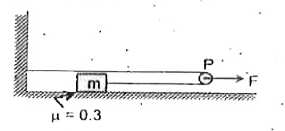
View SolutionA trolley of mass 20 kg is attached to a block of mass 4kg by massless string passing over a frictionless pulley as shown in the figure. If the coefficient of kinetic friction between trolley and the surface is 0.02, then the acceleration of the trolley and block system is (Takeg=10ms−2)

View SolutionTwo blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.

View SolutionA block of mass 3kg which is on a smooth inclined plane making angie of 30∘ to the horizontal is connected by cord passing over light frictionless pulley to second block of mass 2kg hanging vertically. What is the acceleration of each block and waht is the tension of the cord ? .
View Solution
