A block of metal of mass 2 kg on a horizontal table is attached to a mass of 0.46 kg by a light string passing over a frictionless pulley at the edge of the table. The block is subjected to a horizontal force by allowing the 0.45 kg mass to fall . The coefficient of sliding friction between the block and table is 0.2.
Calculate
the initial acceleration

Mass of first block , m1=0.45kg
Mass of second block , m2=2kg
coefficient of sliding friction between the block and table , μ=0.2
Initial acceleration , a (m1−μm2m1+m2)g
⇒a=(0.45−0.2×20.45+2)×9.8
⇒a=0.2ms−2
Topper's Solved these Questions
- LAWA OF MOTIONBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - LAWA OF MOTIONEXERCISE - ADDITIONAL PROBLEMS
22 Videos
- KINETIC THEORYBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - KINETIC THEORYEXERCISE - Additional Problems
5 Videos
- LAWS OF MOTIONBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - LAWS OF MOTIONEXERCISE - LONG ANSWER QUESTIONS
3 Videos
Similar Questions
A block A of mass m1 rests on a horizontal table. A light string connected to it passes over a frictionless pulley at the edge of table and from its other end another block B of mass m2 is suspended. The coefficient of knetic friction between the block and table is μk . When the block A is sliding on the table, the tension in the string is.
View SolutionA block of mass M placed on a frictionless horizontal table is pulled by another block of mass m hanging vertically by a massless string passing over a frictionless pulley. The tension in the string is :
View Solution
Knowledge Check
A block A of mass m1 rests on a horizontal table. A light string connected to it passes over a frictionless pully at the edge of the table and from its other end another block B of mass m2 is suspended. The coefficient of kinetic friction between the block and the table is H. When the block A is sliding on the table, the tension in the string is
Am1m2(1+μk)g(m1+m2)Bm1m2(1−μk)g(m1)+m2C(m2+μkm1)g(m1+m2)D(m2−μkm1)g(m1+m2)A block A of mass m1 rests on a horizontal table. A light string connected to it passes over a frictionless pulley at the edge of table and from its other end another block B of mass m2 is suspended. The coefficient of knetic friction between the block and table is μk . When the block A is sliding on the table, the tension in the string is.
A(m2+μkm1)gm1+m2B(m2−μkm1)gm1+m2Cm1m2(1+μk)g(m1+m2)Dm1m2(1−μk)g(m1+m2)A block of mass M placed on a frictionless horizontal table is pulled by another block of mass m hanging vertically by a massless string passing over a frictionless pulley. The tension in the string is :
AmM+mgBMM+mgCM+mmngDMnM+ng
A body of mass 20 kg is resting on a table. A light string is attached to it and passed over a smooth pulley at the edge of the table and a mass 3kg is attached at the free end. What is the acceleration of the system of the coefficient of kinetic friction between the mass and the table is 0.04 ? What is the tension in the string ?
View SolutionA horizontal force of 4 N is applied to a block of mass 2 kg resting on a frictionless table. What is the acceleration of the block in ms−2 ?
View SolutionTwo masses A and B of 15 kg and 10 kg are connected with a string passing over a frictionless pulley fixed at the corner of a table (as shown in figure). The coefficient of friction between the table and block is 0.4. The minimum mass of C, that may be placed on A to prevent it from moving is:
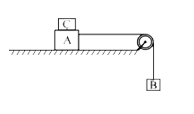
View SolutionA block of mass 4 kg is resting on a horizontal table and a force of 10 N is applied on it in the horizontal direction. The coefficient of kinetic friction between the block and the table is 0.1. The work done in √20 s
View SolutionTwo masses A and B of 15 kg and 10 kg are connected with a string passing over a frictionless pulley fixed at the corner of a table (as shown in figure). The coefficient of friction between the table and block is 0.4. The minimum mass of C, that may be placed on A to prevent it from moving is:

View Solution
