A block of mass M placed on a frictionless horizontal table is pulled by another block of mass m hanging vertically by a massless string passing over a frictionless pulley. The tension in the string is :
mM+mg
MM+mg
M+mmMg
MmM+mg
The correct Answer is:D
To find the tension in the string connecting a block of mass M on a frictionless table and a block of mass m hanging vertically, we can follow these steps:
Step 1: Analyze the Forces on Each Block
- For the block of mass M on the table:
- The only horizontal force acting on it is the tension T in the string.
- According to Newton's second law, we can write the equation:
T=M⋅a(1)
- For the hanging block of mass m:
- The forces acting on it are the gravitational force mg downward and the tension T upward.
- The net force acting on this block can be expressed as:
mg−T=m⋅a(2)
Step 2: Set Up the Equations
From equation (1), we have:
T=M⋅a
From equation (2), we can rearrange it to express T:
T=mg−m⋅a
Step 3: Solve for Acceleration
Now, we can set the two expressions for T equal to each other:
M⋅a=mg−m⋅a
Rearranging gives:
M⋅a+m⋅a=mg
a(M+m)=mg
a=mgM+m
Step 4: Substitute Back to Find Tension
Now that we have a, we can substitute it back into equation (1) to find the tension T:
T=M⋅a=M⋅(mgM+m)
T=M⋅m⋅gM+m
Final Result
Thus, the tension in the string is given by:
T=M⋅m⋅gM+m
- For the block of mass M on the table:
- The only horizontal force acting on it is the tension T in the string.
- According to Newton's second law, we can write the equation:
T=M⋅a(1)
- For the hanging block of mass m:
- The forces acting on it are the gravitational force mg downward and the tension T upward.
- The net force acting on this block can be expressed as:
mg−T=m⋅a(2)
From equation (1), we have:
T=M⋅a
T=mg−m⋅a
Now, we can set the two expressions for T equal to each other:
M⋅a=mg−m⋅a
M⋅a+m⋅a=mg
a(M+m)=mg
a=mgM+m
Now that we have a, we can substitute it back into equation (1) to find the tension T:
T=M⋅a=M⋅(mgM+m)
T=M⋅m⋅gM+m
Thus, the tension in the string is given by:
T=M⋅m⋅gM+m
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 249videos
DYNAMICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 2 ( NUMERICAL TYPE FOR JEE MAIN )16videos
DYNAMICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 0 (LONG ANSWER TYPE)4videos
DYNAMICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE68videos
DC CIRCUIT
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-G10videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
Similar Questions
Figure shows three blocks of mass m each hanging on a string passing over a pulley. Calculate the tension in the string connecting A to B and B to C?
 View Solution
View SolutionA block of mass m1=2 kg is kept on a smooth horizontal table. Another block of mass m2=1 kg is connected to m1 by a light inextensible string passing over a smooth pulley as shown in the figure. If the blocks are released, what will be the (a) acceleration of each block (b) tension in the string?
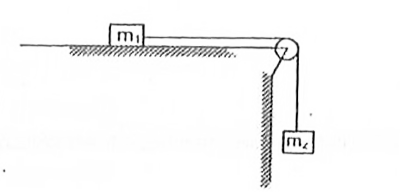 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m
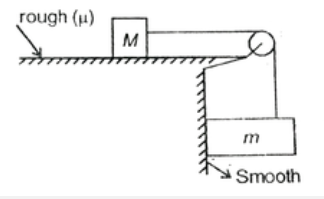
The minimum value of coefficient of friction μ such that system remains at rest , isView SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string passing over a smooth pulley. The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m
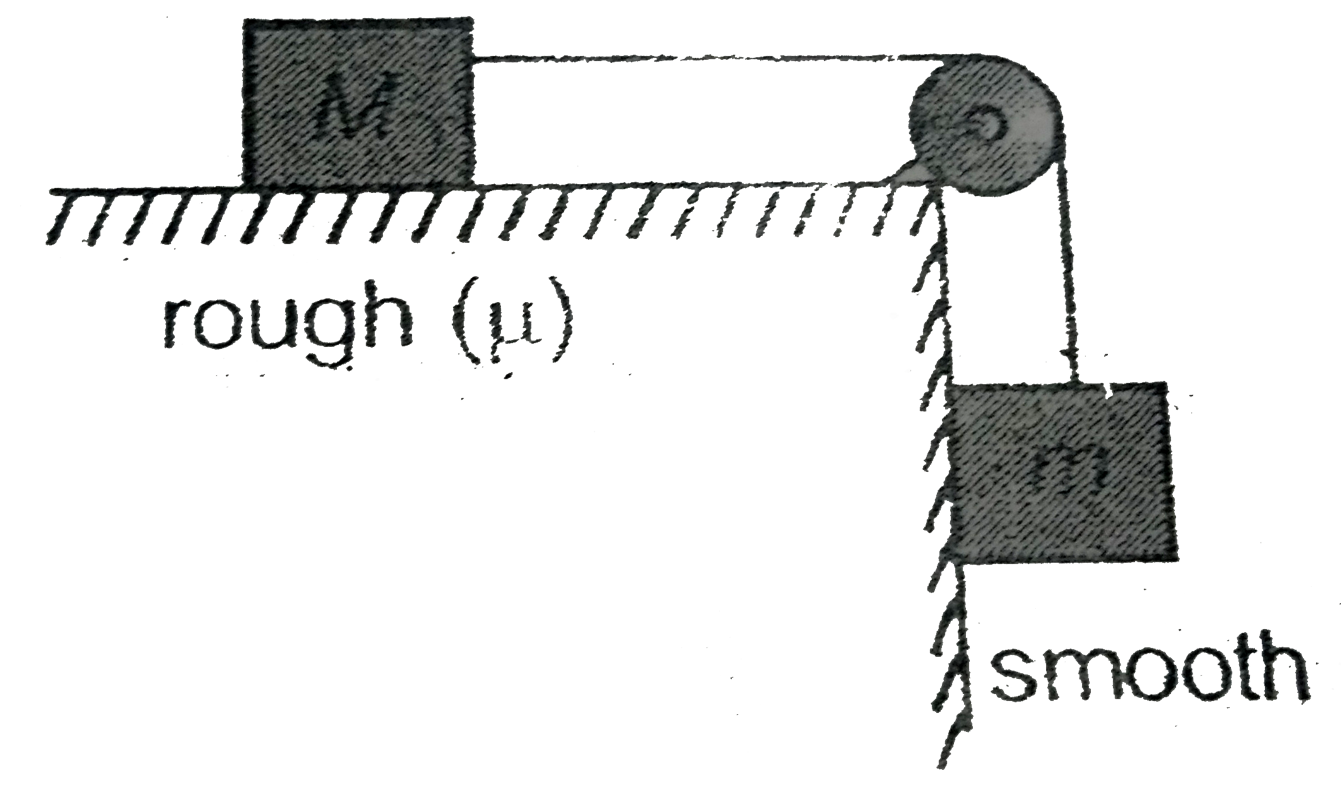
If the whole system ( horizontal surface + blocks ) accelerates towards right the value of maximum on the horizontal surface isView SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string passing over a smooth pulley. The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m

If the coefficient of friction of friction μ is less than the above value, then downward acceleration of block m isView SolutionTwo bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View SolutionA string is used to pull a block of mass m vertically up by a distance h at a constant acceleration g3. The work done by the tension in the string is
View SolutionA block A of mass 14 kg moves alongg an inclined plance that makes an angle of 30∘ with the horizontal . This block is connected to another block B of mass 14 kg by a taut massless string that runs around a massless frictionless pulley . The block B moves down with constant velocity . Calculate force of friction and coefficient of kinetic friction .
View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View Solution

