A block of volume V and density ρ is floating in a liquid of density 2ρ filled in a vessel. Now the vesset starts falling freely with acceleration g. Then the volume of block inside the liquid in the falling condition is
V
V/2
arbitray
zero
The correct Answer is:C
To solve the problem step-by-step, we will analyze the situation of the block floating in the liquid both when the vessel is at rest and when it is falling freely.
Step 1: Understand the Initial Condition
- The block has a volume V and density ρ.
- The liquid has a density 2ρ.
- When the block is floating in the liquid at rest, the weight of the block is balanced by the buoyant force acting on it.
Step 2: Calculate the Weight of the Block
- The weight of the block W can be calculated as:
W=mass×g=ρVg
Step 3: Calculate the Buoyant Force
- The buoyant force Fb acting on the block is given by Archimedes' principle:
Fb=density of liquid×g×volume displaced
- Let the volume of the block submerged in the liquid be Vd. Since the density of the liquid is 2ρ, we have:
Fb=2ρgVd
Step 4: Set Up the Equation for Equilibrium
- At equilibrium (when the vessel is not falling), the weight of the block equals the buoyant force:
ρVg=2ρgVd
- Dividing both sides by g and ρ (assuming g≠0 and ρ≠0):
V=2Vd
- Thus, the volume of the block submerged is:
Vd=V2
Step 5: Analyze the Condition When the Vessel is Falling Freely
- When the vessel falls freely with acceleration g, the effective gravitational force acting on the block is zero because both the block and the liquid are in free fall.
- In this condition, the buoyant force becomes zero because the pressure difference that creates buoyancy is eliminated.
Step 6: Conclusion on the Volume of the Block Inside the Liquid
- Since the buoyant force is zero, the block will not be forced down into the liquid. Therefore, the volume of the block that is submerged can be arbitrary.
- The block can float at any position within the liquid, meaning the volume submerged can be anywhere from 0 to V.
Final Answer
The volume of the block inside the liquid in the falling condition is arbitrary.
---
- The block has a volume V and density ρ.
- The liquid has a density 2ρ.
- When the block is floating in the liquid at rest, the weight of the block is balanced by the buoyant force acting on it.
- The weight of the block W can be calculated as:
W=mass×g=ρVg
- The buoyant force Fb acting on the block is given by Archimedes' principle:
Fb=density of liquid×g×volume displaced
- Let the volume of the block submerged in the liquid be Vd. Since the density of the liquid is 2ρ, we have:
Fb=2ρgVd
- At equilibrium (when the vessel is not falling), the weight of the block equals the buoyant force:
ρVg=2ρgVd
- Dividing both sides by g and ρ (assuming g≠0 and ρ≠0):
V=2Vd
- Thus, the volume of the block submerged is:
Vd=V2
- When the vessel falls freely with acceleration g, the effective gravitational force acting on the block is zero because both the block and the liquid are in free fall.
- In this condition, the buoyant force becomes zero because the pressure difference that creates buoyancy is eliminated.
- Since the buoyant force is zero, the block will not be forced down into the liquid. Therefore, the volume of the block that is submerged can be arbitrary.
- The block can float at any position within the liquid, meaning the volume submerged can be anywhere from 0 to V.
The volume of the block inside the liquid in the falling condition is arbitrary.
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced
57 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct
21 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
Similar Questions
Knowledge Check
The pressure inside a liquid of density ρ at a depth h is :
AhρgBhρgChρgDhρ
A block of density ρ floats in a liquid with its one third volume immersed. The density of the liquid is
View SolutionA ball of volume V and density ρ1 is moved downwards by a distance 'd' in liquid of density ρ2. Find total change in potential energy of the system.

View SolutionA drop of liquid of density ρ is floating half-immersed in a liquid of density d. If σ is the surface tension the diameter of the drop of the liquid is
View SolutionA solid of density D is floating in a liquid of density d. If υ is the volume of solid submerged in the liquid and V is the total volume of the solid, then υ/V equal to
View SolutionA cubical block is floating in a liquid with one fourth o its volume immersed in the liquid. If whole of the system accelerates upward with acceleration g/4, the fraction of volume immersed in the liquid will be :-
View SolutionA ball of mass m and density ρ2 is completely immersed in a liquid of density ρ, contained in an accelerating vessel as shown.Select the correct answer using the codes given below the columns.
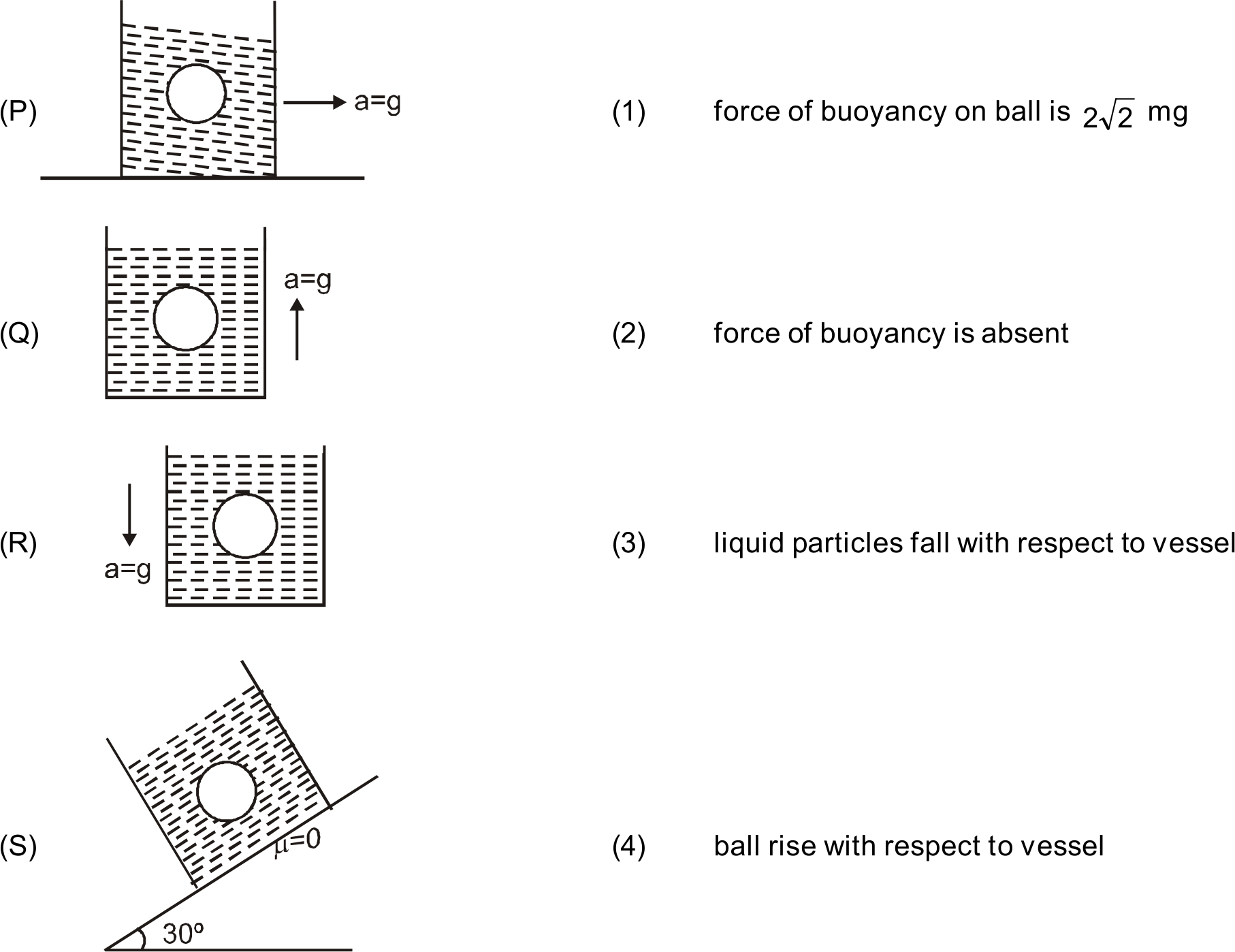
View SolutionA body of volume V and density ρ is kept completely immersed in a liquid of density ρL. If g is the acceleration due to gravity, write expressions for the following
(i) the weight of the body.
(ii) the upthrust on the body.
(iii) the apparent weight of the body in liquid,
(iv) the loss in weight of the body.
View Solution
