A ball of density is released from deep inside of a liquid of density . It will move up
with an increasing acceleration
with a decreasing acceleration
with a constant acceleration
with zero acceleration
The correct Answer is:B
To solve the problem of a ball of density ρ released from deep inside a liquid of density 2ρ, we can analyze the forces acting on the ball and determine its motion. Here’s a step-by-step solution:
Step 1: Identify the Forces Acting on the Ball
When the ball is submerged in the liquid, two main forces act on it:
1. Weight of the Ball (W): This is the gravitational force acting downwards.
W=m⋅g=V⋅ρ⋅g
where V is the volume of the ball, ρ is the density of the ball, and g is the acceleration due to gravity.
2. Buoyant Force (F_B): This is the upward force exerted by the liquid on the ball.
FB=V⋅(2ρ)⋅g
where 2ρ is the density of the liquid.
Step 2: Calculate the Net Force
The net force Fnet acting on the ball can be calculated as:
Fnet=FB−W
Substituting the expressions for FB and W:
Fnet=(V⋅(2ρ)⋅g)−(V⋅ρ⋅g)
Fnet=V⋅g⋅(2ρ−ρ)=V⋅g⋅ρ
Step 3: Determine the Direction of Motion
Since Fnet is positive (as V⋅g⋅ρ is positive), the net force is directed upwards. This means that the ball will accelerate upwards.
Step 4: Analyze the Acceleration
The acceleration a of the ball can be found using Newton's second law:
Fnet=m⋅a
Substituting m=V⋅ρ:
V⋅g⋅ρ=(V⋅ρ)⋅a
Dividing both sides by V⋅ρ (assuming V⋅ρ≠0):
g=a
This indicates that the ball will accelerate upwards with an acceleration equal to g.
Step 5: Conclusion
Since the ball is less dense than the liquid, it will rise to the surface of the liquid. The acceleration of the ball remains constant as it moves upward.
Final Answer
The ball will move up with a constant acceleration equal to g.
---
When the ball is submerged in the liquid, two main forces act on it:
1. Weight of the Ball (W): This is the gravitational force acting downwards.
W=m⋅g=V⋅ρ⋅g
where V is the volume of the ball, ρ is the density of the ball, and g is the acceleration due to gravity.
FB=V⋅(2ρ)⋅g
where 2ρ is the density of the liquid.
The net force Fnet acting on the ball can be calculated as:
Fnet=FB−W
Substituting the expressions for FB and W:
Fnet=(V⋅(2ρ)⋅g)−(V⋅ρ⋅g)
Fnet=V⋅g⋅(2ρ−ρ)=V⋅g⋅ρ
Since Fnet is positive (as V⋅g⋅ρ is positive), the net force is directed upwards. This means that the ball will accelerate upwards.
The acceleration a of the ball can be found using Newton's second law:
Fnet=m⋅a
Substituting m=V⋅ρ:
V⋅g⋅ρ=(V⋅ρ)⋅a
Dividing both sides by V⋅ρ (assuming V⋅ρ≠0):
g=a
This indicates that the ball will accelerate upwards with an acceleration equal to g.
Since the ball is less dense than the liquid, it will rise to the surface of the liquid. The acceleration of the ball remains constant as it moves upward.
The ball will move up with a constant acceleration equal to g.
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced
57 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct
21 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
Similar Questions
A small ball of density rho_(0) is released from the surface of a liquid whose density varies with depth h as ρ=ρ02(α+βh). Mass of the ball is m. Select the most appropriate one option.
View SolutionA ball of density ρ is dropped from a height on the surface of a non-viscous liquid of density 2ρ. Choose the correct options.

View Solution
Knowledge Check
The pressure inside a liquid of density ρ at a depth h is :
AhρgBhρgChρgDhρ
A ball of density ρ0 falls from rest from a point P onto the surface of a liquid of density ρ in the time T. It enters the liquid, stops, moves up, and returns to P in a total time 3 T. neglect viscosity, surface tension and splashing find the ratio of ρρ0
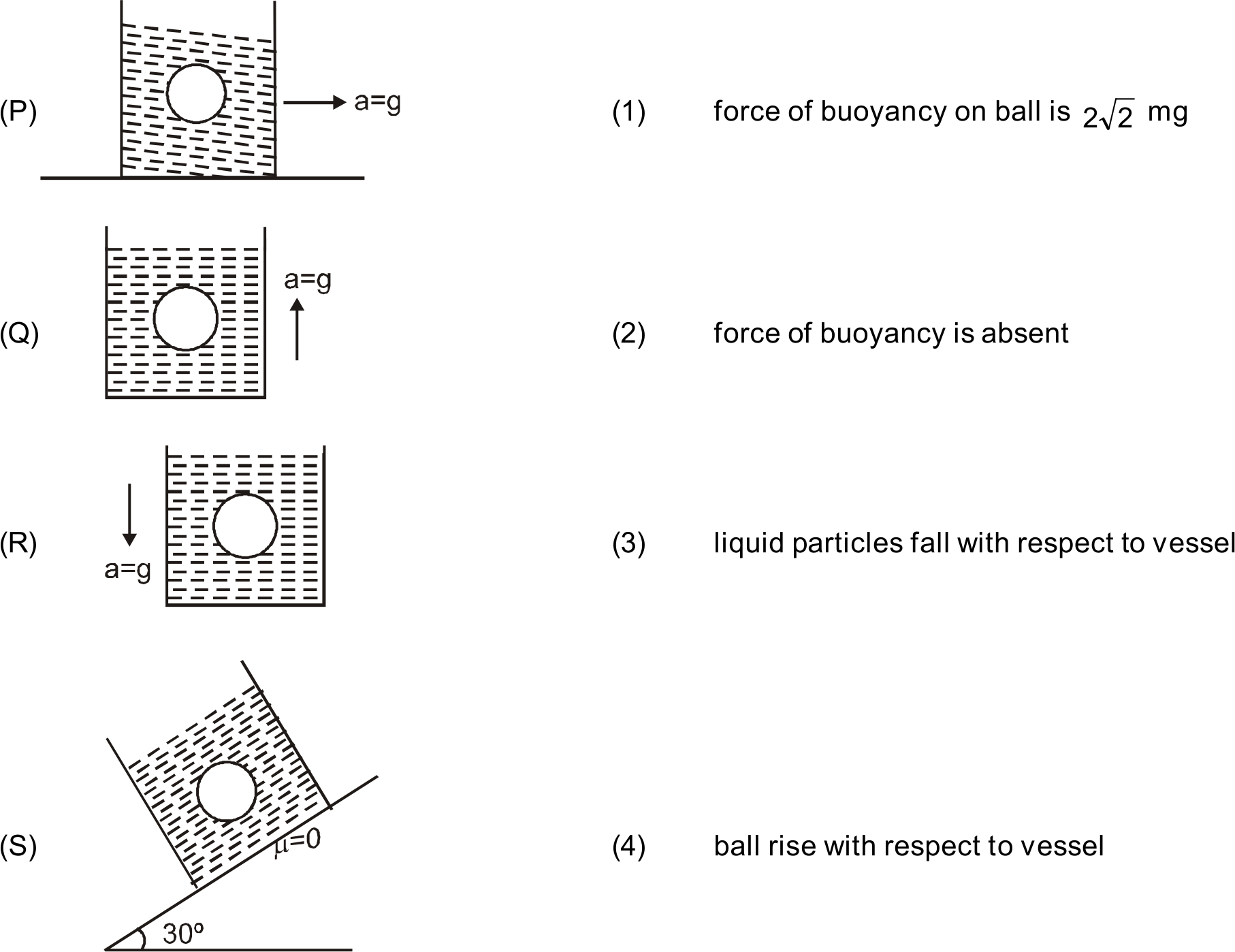
View SolutionA ball of mass m and density ρ2 is completely immersed in a liquid of density ρ, contained in an accelerating vessel as shown.Select the correct answer using the codes given below the columns.
View SolutionA ball of mass m and density ρ is immersed in a liquid of density 3ρ at a depth h and released. To what height will the ball jump up above the surface of liqud ? (neglect the reistance of water and air).
View SolutionA small ball of density ρ is immersed in a liquid of density σ(>ρ) to a depth h and released. The height above the surface of water up to which the ball will jump is
View SolutionA block of volume V and density ρ is floating in a liquid of density 2ρ filled in a vessel. Now the vesset starts falling freely with acceleration g. Then the volume of block inside the liquid in the falling condition is
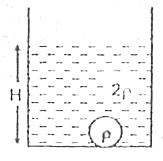
View SolutionA small ball of density ρ is placed from the bottom of a tank in which a non viscous liquid of density 2ρ is filled . Find the time taken by the ball to reach the surface of liquid and maximum height reached above the bottom of container . (Size of the ball and any type of drag force acting on the ball are negligible )
View SolutionA drop of liquid of density ρ is floating half-immersed in a liquid of density d. If σ is the surface tension the diameter of the drop of the liquid is
View Solution
