A block sliding down on an inclined plane forms an angle $θ$ with the horizontal. The friction coefficient depends on the distance $x$ covered as $μ = k x$ , where $k$ is a constant. Find the distance covered by the block till it stops and its maximum velocity over this distance. Also , sketch a graph between square of velocity and distance covered $x$ .

Video Solution

Text Solution

Verified by Experts

$μ = k x$
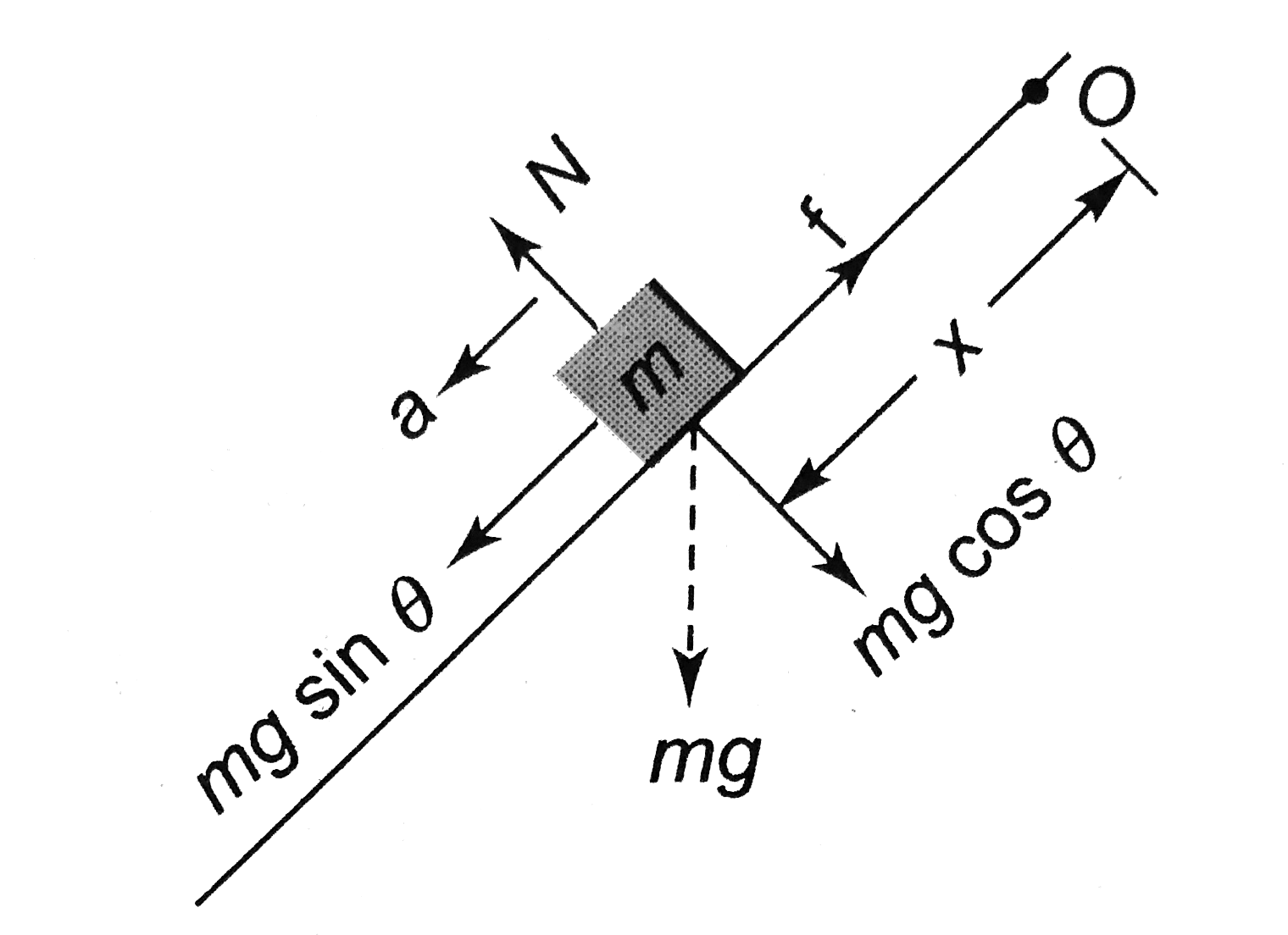
$N = m g cos θ, f = μ N = μ m g cos θ$
Along the plane : $m g sin θ - μ m g cos θ = m a$
$a = g sin θ - μ g cos θ$
$μ = k x$
$a = g sin θ - k g x cos θ$
$v \frac{d v}{d x} = g sin θ - k g x cos θ$
$\int_{0}^{v} v d v = \int_{0}^{x} (g sin θ - k g x cos θ) d x$
$v^{2} = 2 g sin θ x - k g x^{2} cos θ$
When the block stops , $v = 0$
$0 = 2 f sin θ x - k g x^{2} cos θ$
When the block stops , $v = 0$
$0 = 2 g sin θ x - k g x^{2} cos θ$
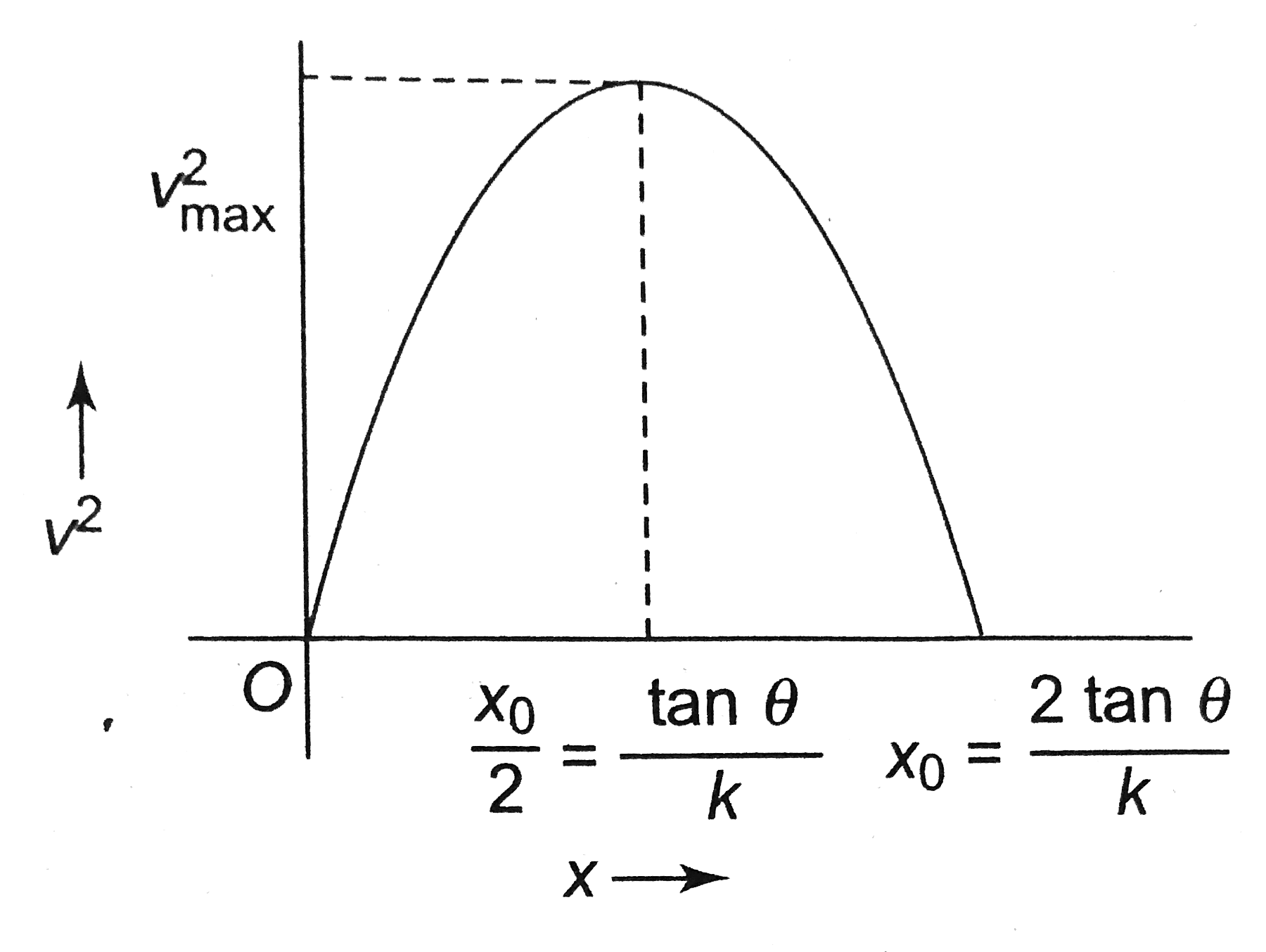
$x = x_{0} = \frac{2 tan θ}{k}$
Velocity will be maximum when $a = 0$
$a = g sin θ - k g x cos θ$
$0 = g sin θ - k g x cos θ \Rightarrow x = \frac{tan θ}{k} = \frac{x_{0}}{2}$
$v_{max}^{2} = 2 g sin θ \frac{tan θ}{k} - k g cos θ \frac{{tan}^{2} θ}{k^{2}}$
$v_{max} = \sqrt{\frac{g}{k} tan θ sin θ}$
$v^{2} v / s x$
$v^{2} = 2 g sin θ x - k g {cos x}^{2}$
Graph : $y = 2 g sin θ x - k g cos θ x^{2}$ ( parabola , coefficient of $x^{2} i s - v e$ , parabola open downward)
Note : (1). From $x = 0 \to x_{0} / 2, m g sin θ > f$ , acceleration its increasing.
2. At $x = x_{0} / 2, m g sin θ = f$ , net force = 0 , the block is in equilibrium , velocity is maximum.
3. $x = x_{0} / 2 \to x_{0}, m g sin θ < f$ , retardation , velocity is decreasing and ultimately teh blocks stops.

Updated on:21/07/2023