A block with base dimension 25cm×50cm and weighing 25 kgf slides down a 30∘ inclined surface with a uniform speed of 2m/sec on a 2mm thin oil film. The viscosity of oil in SI units is

0.25kgfsec/m2
0.1kgfsec/m2
0.08kgfsec/m2
0.5kgfsec/m2
The correct Answer is:B
Step by step video & image solution for A block with base dimension 25 cm xx 50 cm and weighing 25 kgf slides down a 30^(@) inclined surface with a uniform speed of 2m//sec on a 2mm thin oil film. The viscosity of oil in SI units is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced
57 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct
21 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
Similar Questions
A block of iron has dimensions 2 m x 0.5 m x 0.25 m. The density of iron is 7.8gcm−3 . Find the mass of block.
View SolutionA small block of mass 2kg is kept on a rough inclined surface of inclination θ=30∘ fixed in a lift. The lift goes up with a uniform speed of 1ms−1 and the block does not slide relative to the inclined surface. The work done by the force of friction on the block in a time interval of 2s is
View SolutionA cubical block of side 10√10 cm is connected to a smooth and uniform disc of mass 20g through an ideal string as shown. The block is placed on a thin liquid layer of thickness 0.2 mm. if center of the disc move downward with constant speed of 2cm/sec after the system is released. If coefficient of viscosity of liquid is x1000 Pa-sec. then find x (Take g=10m/s2)

View SolutionA cubical block (of side 2m) of mass 20kg slides on inclined plane lubricated with the oil of viscosity η=10−1 with constant velocity of 10ms−1. Find out the thickness of the layer of liquid (take g=10ms−2).

View SolutionA cubical block (of sie 2m) of mass 20 kg slides on inclined plane lubricated with the oil of viscosity η=10−1 poise with constant velocity of 10 m/s find out the thickness of layer of liquid (g=10m/s2)
_S01_037_Q01.png)
View Solution
A space 2.5cm wide between two large plane surfaces is filled with oil. Force required to drag a very thin plate of area 0.5m2 just midway the surfaces at a speed of 0.5msec is 1N. The coefficient of viscosity in kg−sm2 is:
View Solution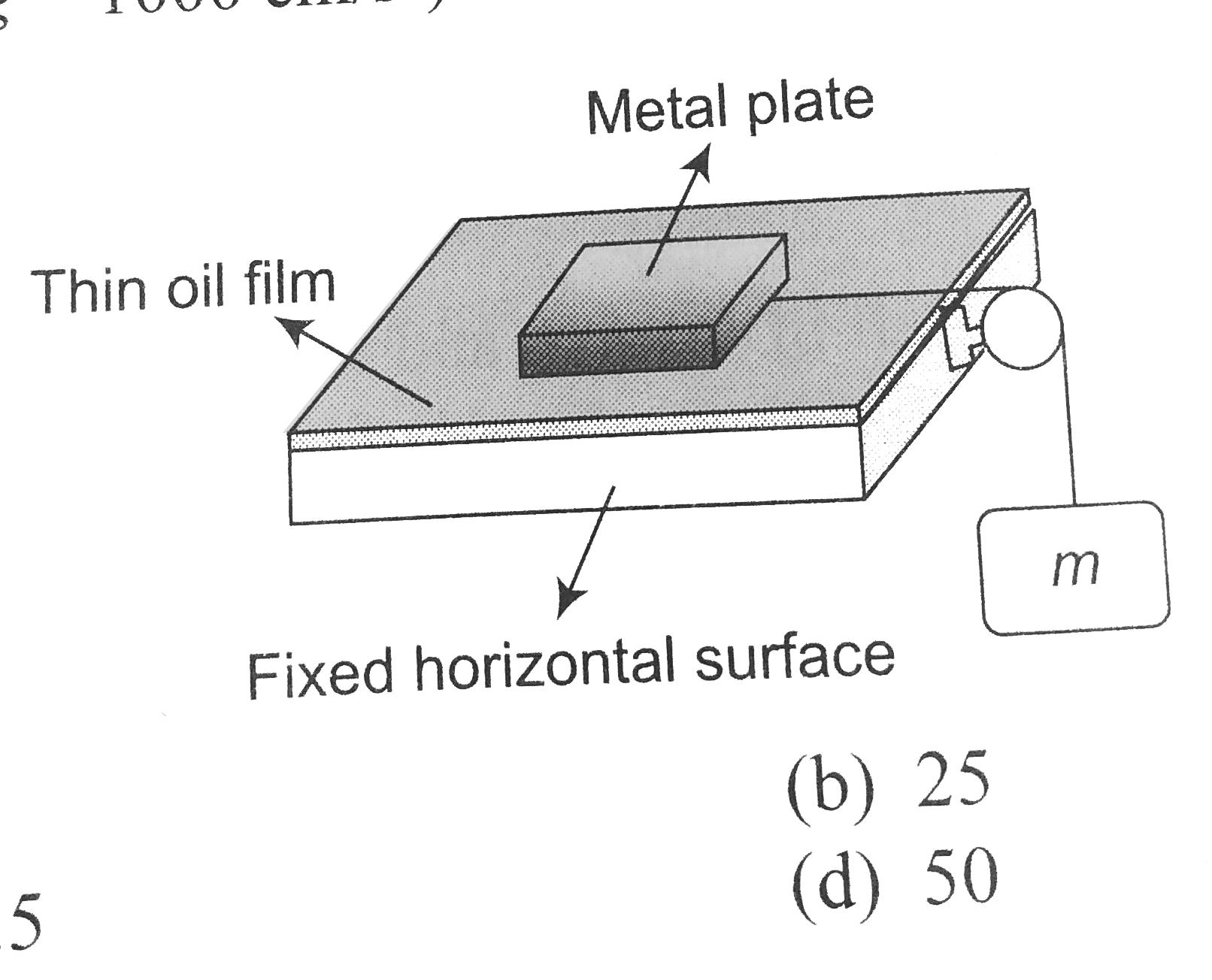
A rectangular metal plate has dimensions of 10cm×20cm. A thin film of oil separates the plate from a fixed horizontal surface. The separation between the rectangular plate and the horizontal surface is 0.2mm. An ideal string is attached to the plate and passes over an ideal pulley to a mass m. When m=125gm, the metal plate moves at constant speed of 5cms, across the horizontal surface. Then the coefficient of viscosity of oil in dyne−scm2 is (Use g=1000cms2)
View SolutionShanti Sweet Stall was placing an order for making carboard boxes for packing their sweets. Two sizes of boxes were required. The bigger of dimensions 25cm×20cm×5cm and the smaller of dimensions 15cm×12cm×5cm. For all the overlaps, 5% of the total surface area is required extra. If the cost of the carboard is Rs. 4 for 1000cm2, find the cost of carboard required for supplying 250 boxes of each kind.
View SolutionShanti Sweet Stall was placing an order for making carboard boxes for packing their sweets. Two sizes of boxes were required. The bigger of dimensions 25cm×20cm×5cm and the smaller of dimensions 15cm×12cm×5cm. For all the overlaps, 5% of the total surface area is required extra. If the cost of the carboard is Rs. 4 for 1000cm2, find the cost of carboard required for supplying 250 boxes of each kind.
View SolutionTwo blocks of masses m1 = 4 kg and m2 = 2kg connected by a massless rod slide down on an inclined plane of inclination 37o as shown in figure. If coefficient of friction of m1 and m2 with inclined plane are μ1 = 0.75 and μ2 = 0.25 respectively, then tension (T) in the rod is (g = 10 ms−2)
View Solution
