Two blocks of masses m1 = 4 kg and m2 = 2kg connected by a massless rod slide down on an inclined plane of inclination 37o as shown in figure. If coefficient of friction of m1 and m2 with inclined plane are μ1 = 0.75 and μ2 = 0.25 respectively, then tension (T) in the rod is (g = 10 ms−2)
165N
163N
0N
3N
The correct Answer is:c
To solve the problem, we need to find the tension (T) in the rod connecting the two blocks sliding down an inclined plane. Let's break it down step by step.
Step 1: Identify the forces acting on each block
For block m1 (4 kg):
- Weight: W1=m1⋅g=4⋅10=40N
- Component of weight parallel to the incline: W1∥=W1⋅sin(37∘)=40⋅sin(37∘)
- Component of weight perpendicular to the incline: W1⊥=W1⋅cos(37∘)=40⋅cos(37∘)
- Frictional force: Ffriction1=μ1⋅W1⊥=0.75⋅W1⊥
For block m2 (2 kg):
- Weight: W2=m2⋅g=2⋅10=20N
- Component of weight parallel to the incline: W2∥=W2⋅sin(37∘)=20⋅sin(37∘)
- Component of weight perpendicular to the incline: W2⊥=W2⋅cos(37∘)=20⋅cos(37∘)
- Frictional force: Ffriction2=μ2⋅W2⊥=0.25⋅W2⊥
Step 2: Calculate the net force acting on the system
The net force acting on the system (both blocks) can be expressed as:
Fnet=(W1∥+W2∥)−(Ffriction1+Ffriction2)
Substituting the expressions for the forces:
Fnet=(m1⋅g⋅sin(37∘)+m2⋅g⋅sin(37∘))−(μ1⋅m1⋅g⋅cos(37∘)+μ2⋅m2⋅g⋅cos(37∘))
Step 3: Calculate the acceleration of the system
Using Newton's second law, the net force can also be expressed as:
Fnet=(m1+m2)⋅a
Setting the two expressions for Fnet equal gives us:
(m1+m2)⋅a=(m1⋅g⋅sin(37∘)+m2⋅g⋅sin(37∘))−(μ1⋅m1⋅g⋅cos(37∘)+μ2⋅m2⋅g⋅cos(37∘))
Step 4: Solve for acceleration (a)
Substituting the values:
- g=10m/s2
- sin(37∘)≈0.6
- cos(37∘)≈0.8
Calculating:
a=(4⋅10⋅0.6+2⋅10⋅0.6)−(0.75⋅4⋅10⋅0.8+0.25⋅2⋅10⋅0.8)4+2
=(24+12)−(24+4)6=36−286=86≈1.33m/s2
Step 5: Calculate the tension (T) in the rod
For block m1:
Using m1:
m1⋅g⋅sin(37∘)−T−Ffriction1=m1⋅a
Substituting the known values:
4⋅10⋅0.6−T−(0.75⋅4⋅10⋅0.8)=4⋅1.33
Solving for T gives:
24−T−24=5.32⟹T=0
Final Answer
The tension T in the rod is 0N.
For block m1 (4 kg):
- Weight: W1=m1⋅g=4⋅10=40N
- Component of weight parallel to the incline: W1∥=W1⋅sin(37∘)=40⋅sin(37∘)
- Component of weight perpendicular to the incline: W1⊥=W1⋅cos(37∘)=40⋅cos(37∘)
- Frictional force: Ffriction1=μ1⋅W1⊥=0.75⋅W1⊥
- Weight: W2=m2⋅g=2⋅10=20N
- Component of weight parallel to the incline: W2∥=W2⋅sin(37∘)=20⋅sin(37∘)
- Component of weight perpendicular to the incline: W2⊥=W2⋅cos(37∘)=20⋅cos(37∘)
- Frictional force: Ffriction2=μ2⋅W2⊥=0.25⋅W2⊥
The net force acting on the system (both blocks) can be expressed as:
Fnet=(W1∥+W2∥)−(Ffriction1+Ffriction2)
Substituting the expressions for the forces:
Fnet=(m1⋅g⋅sin(37∘)+m2⋅g⋅sin(37∘))−(μ1⋅m1⋅g⋅cos(37∘)+μ2⋅m2⋅g⋅cos(37∘))
Using Newton's second law, the net force can also be expressed as:
Fnet=(m1+m2)⋅a
Setting the two expressions for Fnet equal gives us:
(m1+m2)⋅a=(m1⋅g⋅sin(37∘)+m2⋅g⋅sin(37∘))−(μ1⋅m1⋅g⋅cos(37∘)+μ2⋅m2⋅g⋅cos(37∘))
Substituting the values:
- g=10m/s2
- sin(37∘)≈0.6
- cos(37∘)≈0.8
a=(4⋅10⋅0.6+2⋅10⋅0.6)−(0.75⋅4⋅10⋅0.8+0.25⋅2⋅10⋅0.8)4+2
=(24+12)−(24+4)6=36−286=86≈1.33m/s2
For block m1:
Using m1:
m1⋅g⋅sin(37∘)−T−Ffriction1=m1⋅a
Substituting the known values:
4⋅10⋅0.6−T−(0.75⋅4⋅10⋅0.8)=4⋅1.33
Solving for T gives:
24−T−24=5.32⟹T=0
The tension T in the rod is 0N.
Topper's Solved these Questions
Similar Questions
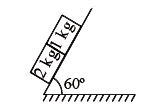
In the figure shown, if friction coefficient of block 1 kg and 2kg with inclined plane is μ1=0.5 and μ2=0.4 respectively, then
View Solution
In the figure shown if friction co-efficient of block 1 and 2 with inclined plane is μ1=0.5 and μ2=0.4 respectively, then find out the correct statement.
View SolutionTwo blocks m1=4 kg and m2=2 kg connected by a weightless rod on a plane having inclination of 37∘ the coefficient of friction of m1 and m2 with the inclined plane are μ=0.25 each. Then the common accleration of the two blocks and the tension in the rod are

View SolutionA block slides down on inclined plane (angle of inclination 60∘ ) with an accelration g/2 Find the coefficient friction

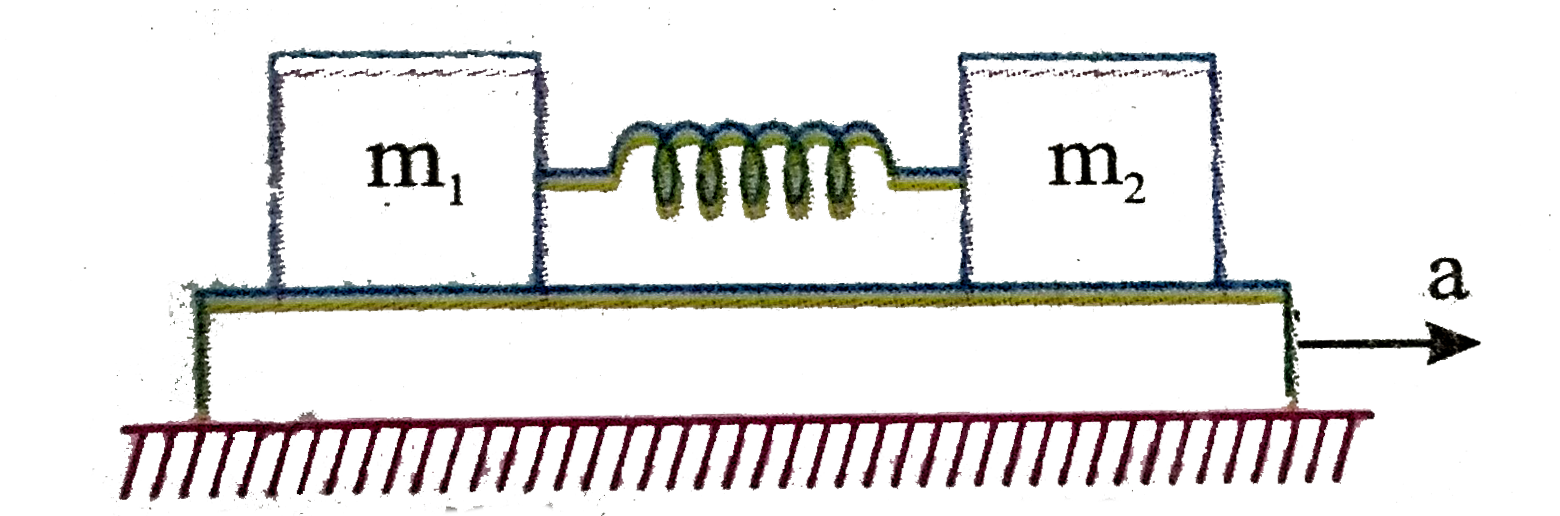
View SolutionTwo block of masses m1 and m2 are connected with a massless unstretched spring and placed over a plank moving with an acceleration 'a' as shown in figure. The coefficient of friction between the blocks and platform is μ
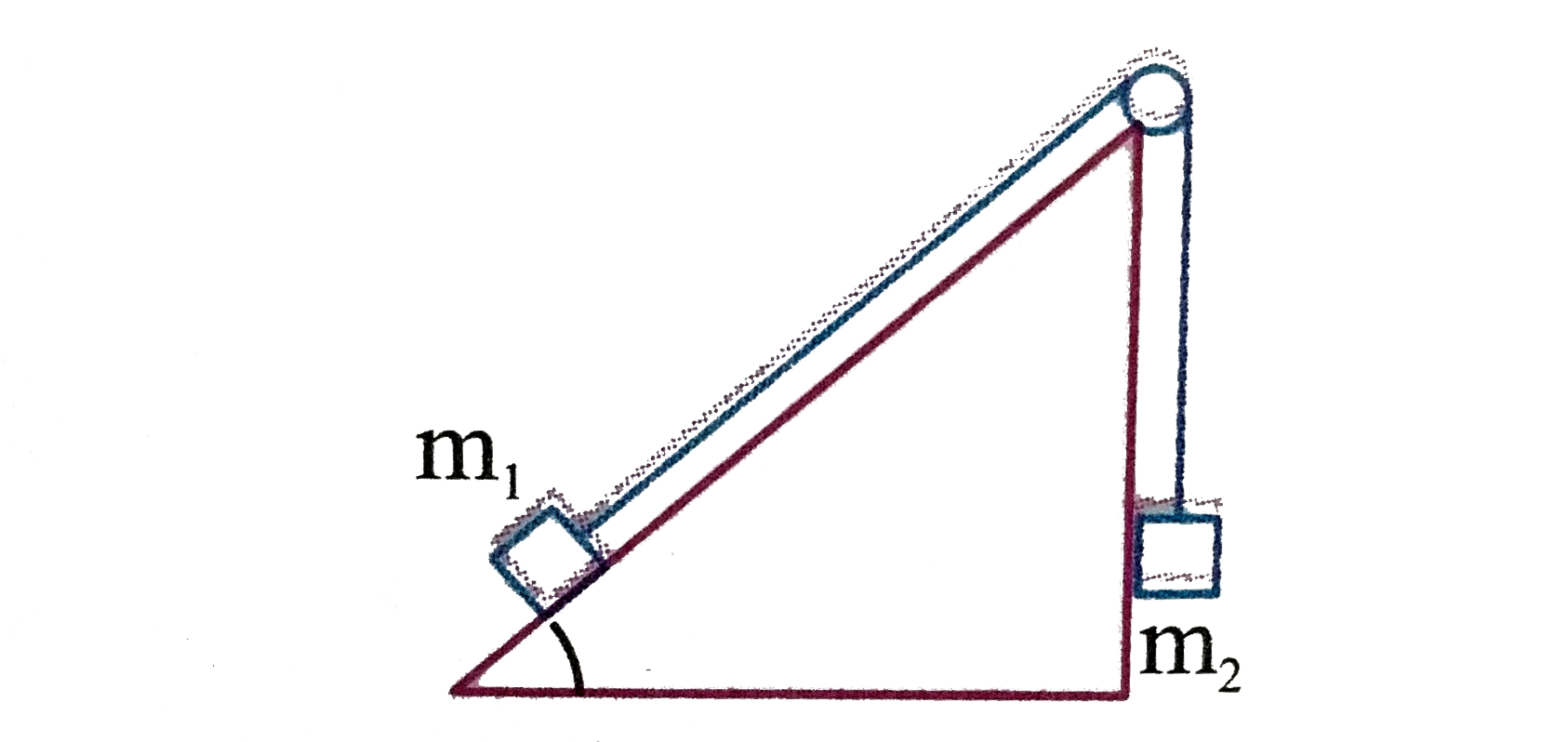
View SolutionTwo blocks of masses m1 and m2 are connected by a string of negligible mass which pass over a frictionless pulley fixed on the top of an inclined plane as shown in figure. The coefficient of friction between m1 and plane is μ.
View SolutionA block of mass m moves with constant speed down the inclined plane of inclination θ. Find the coefficient of kinetic friction.

View SolutionA block of mass m slides down a rough inclined plane with an acceleration g2

View SolutionA block of mass 2 kg slides down an incline plane of inclination 30°. The coefficient of friction between block and plane is 0.5. The contact force between block and plank is :
View Solution
Two blocks of masses m1 and m2 connected by a string are placed gently over a fixed inclined plane, such that the tension in the connecting string is initially zero. The coefficient of friction between m1 and inclined plane is μ1, between m2 and the inclined plane is μ2. The tension in the string shall continue to remain zero if
View Solution
