A boat moves relative to water with a velocity v which is n times less than the river flow velocity u. At what angle to the stream direction must the boat move to minimize drifting ?
In this case, the velocity of boat is less than the river flow velocity. Hence, boat cannot reach the point directly opposite to its starting point, i.e., drift can never be zero.
Suppose the boat starts at an angle θ from the normal diraction up stream as shown in (Fig. 5.90).
Component of the velocity of boat along the river,
vx=u−vsinθ
and velocity perpendicular to the river, vy=vcosθ
time taken to cross the river is t=dvy=dvcosθ
Drift x=(vx)t=(u−vsinθ)dvcosθ=udvsecθ−dtanθ
The drift x is minimum when dxdθ=0
or (udv)(secθ.tanθ)−dsec2θ=0
or uvsinθ=1⇒sinθ=vu
i.,e., for minimum drift, the boat must move at an angle θ=sin−1θ
=sin−1(vu)=sin−1(1)n from the normal direction.
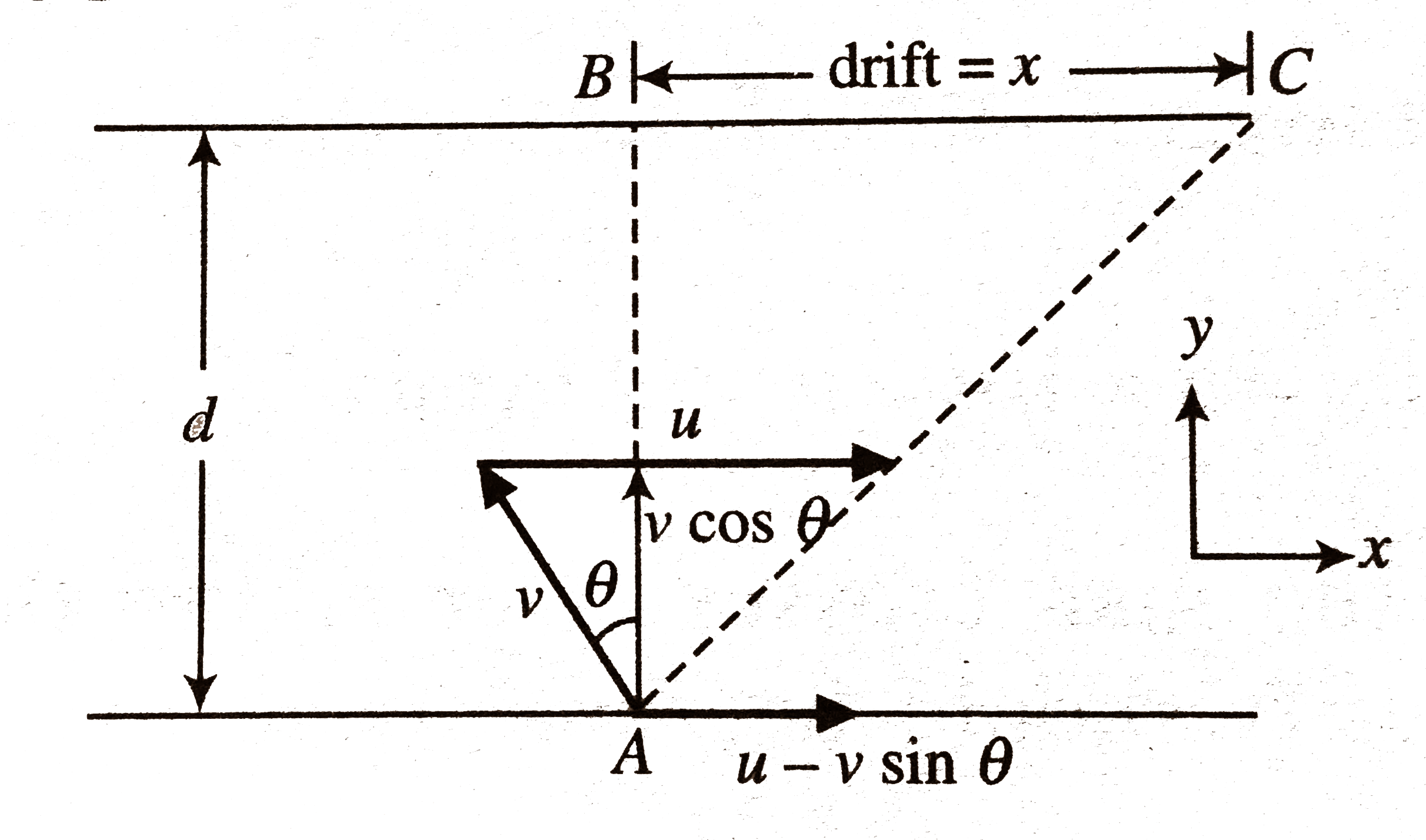 .
.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Solved Examples7videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.115videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
Similar Questions
A boat moves relative to water with a velocity which is n=2.0 times less than the river flow velocity. At what angle to the stream direction must the boat move to minimize drifting?
View SolutionA boat moves in still water with a velocity which is k times less than the river flow velocity. Find the angle to the stream direction at which the boat should be rowed to minimize drifting.
View Solution
Knowledge Check
- Question 1 - Select One
A boat moves relative to water with a velocity which is n=2.0 times less than the river flow velocity. At what angle to the stream direction must the boat move to minimize drifting?
Aπ/2Bsin−1(1/n)Cπ2+sin−1(1/n)Dπ2−sin−1(1/n) - Question 2 - Select One
A boat moves relative to water with a velocity v and river is flowing with 2v. At what angle the boat shall move with the stream to have minimum drift?
A30∘B60∘C90∘D120∘ - Question 3 - Select One
A boat crossing a river moves with a velocity v relative to still water. The river is flowing with a velocity v/2 with respect to the bank. The angle with respect to the flow direction with which the boat should move to minimize the drift is–
A30∘B60∘C150∘D120∘
The velocity of boat relative to water is 4msec . The velocity of water relative to ground is 8msec. In what direction boatman aims the boat to cross the river in minimum drift distance method.
View SolutionA boat stems in a river with velocity 2ˆi+ˆj with respecitve to the ground. The river water flows with a velocity −3ˆi−4ˆj with respect to the ground. What is the relative velocity of boat w.r.t river water ?
View SolutionShow that the direction of the shortest route is at right angles to the river when the velocity of the swimmer is greater than that of the river. Show also that when the velocity of the swimmer is less than that of the river, the direction is tan−1v/√u2−v2 where v= velocity of swimmer and u= velocity of river.
View SolutionA man can row a boat in still water with a velocity of 8kmph.Water is flowing in a river with a velocity of 4kmph. At what angle should he row the boat so as to reach the exact opposite point
View SolutionA boat is moving with a velocity 2i + 3j with respect to ground. The water in the river is moving with a velocity -2i - 3j with respect to ground. The relative velocity of the boat with respect to water is
View Solution

