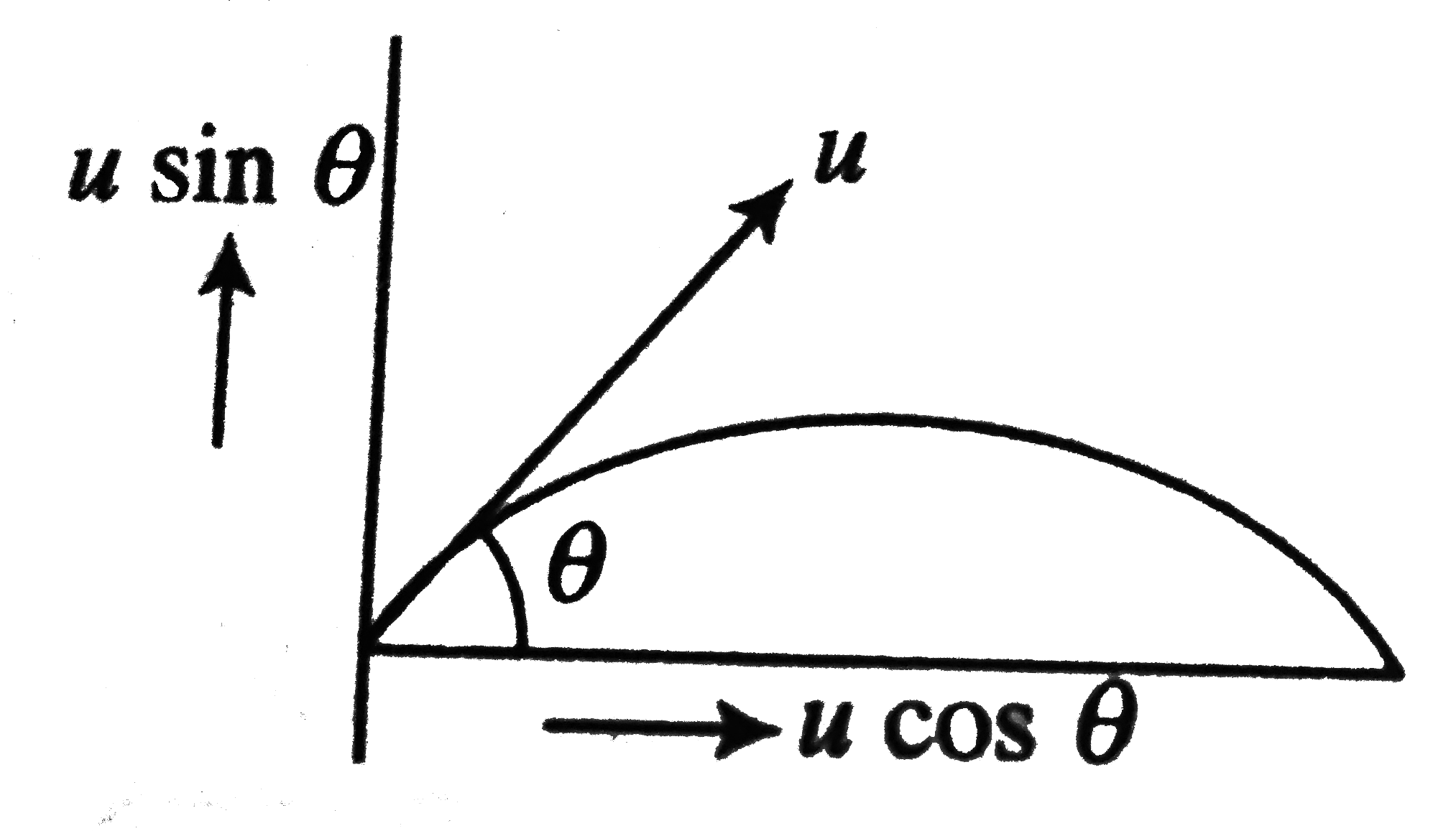
A particle is projected with velocity u at angle θ with horizontal. Find the time when velocity vector is perpendicular to initial velocity vector.
Video Solution
Text Solution
The correct Answer is:(4)
Initial velocity
u=ucosθˆi+usinθˆj
Velocity after time t is
v=ucosθˆi+(usinθ−gt)ˆj
Since uandv are perpendicular to each other, therefore,
→u.→v=0
(ucosθˆi+usinθˆj)×[ucosθˆi+(usinθ−>)ˆj]=0
u2cos2θ+u2sin2θ−usinθgt=0
t=ugsinθ=2010×12=4s.
 .
.
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A particle is projected with a velocity u making an angle θ with the horizontal. At any instant its velocity becomes v which is perpendicular to the initial velocity u. Then v is
AucosθButanθCusecθDucotθ - Question 2 - Select One
A particle is thrown with a speed u at an angle θ with horizontal. After how much time the velocity of particle will be perpendicular to the initial motion of direction
AugcosθBugsinθCusinθgDucosθg - Question 3 - Select One
A particle is projected with velocity v at an angle of θ with horizontal. The average angular velocity of the particle from the point of projection to impact equals:
AgcosθθvBgvsinθCgvθDgθvsinθ
A projectile is projected with velocity u making angle θ with horizontal direction, find : time of flight.
View SolutionA projectile is projected with velocity u making angle θ with horizontal direction, find : horizontal range.
View SolutionA particle is projected form ground with velocity u ar angle θ from horizontal. Match the following two columns.
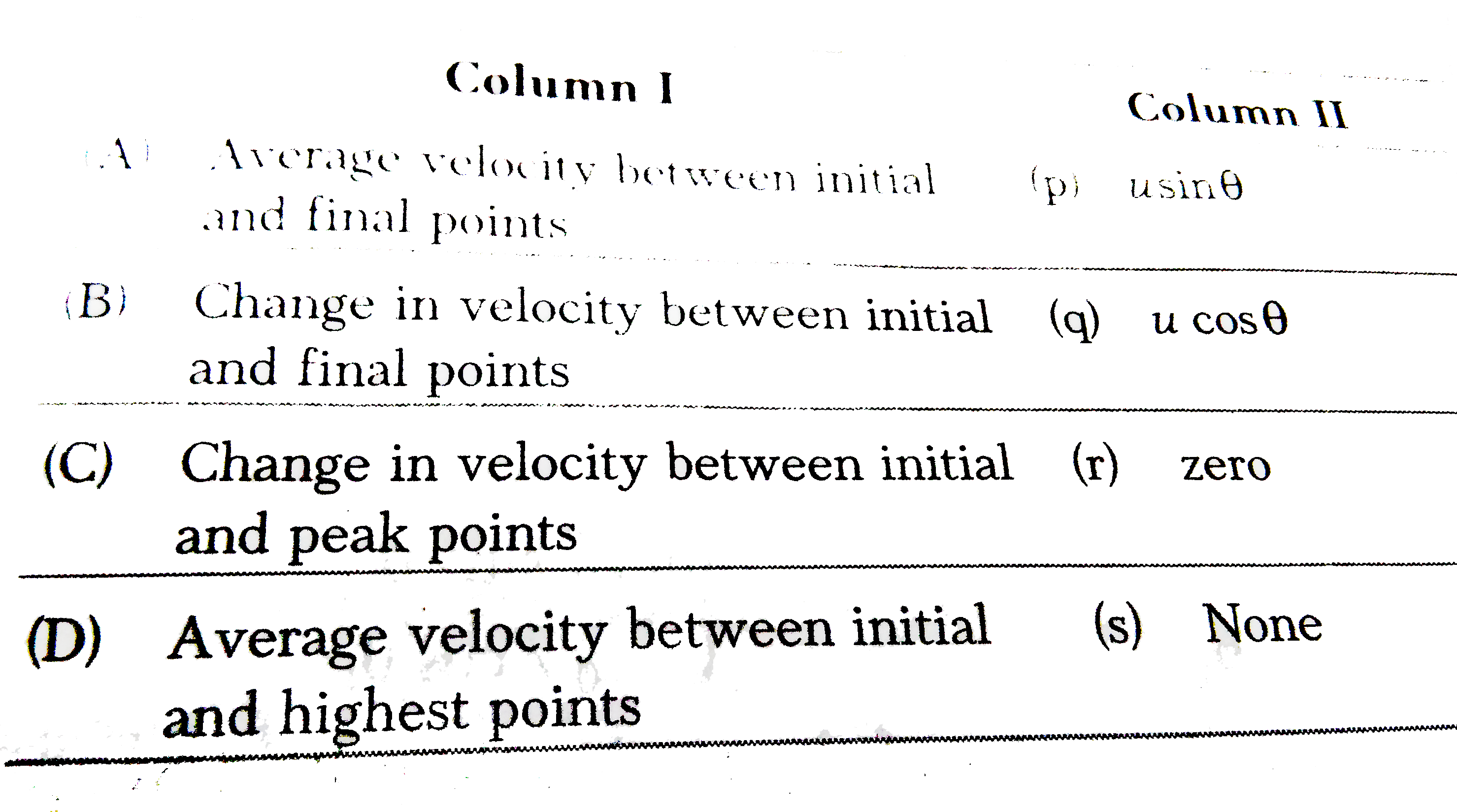 View Solution
View SolutionA particle is projected with velocity v at an angle θ aith horizontal. The average angle velocity of the particle from the point of projection to impact equals
View SolutionMatch the following

In groung to ground projection a particle is projected at 53∘ from horizontal. At t=25 sec after projection, its velocity vector becomes perpendicular to its initial velocity vector.
(Given →a=g⏐↓=10m/s2)View Solution


