A boat moves relative to water with a velocity with a velocity v is n times less than the river flow u. At what angle to the stream direction must the boat move to minimize drifting ?
in this problem . One thing should be carefully noted of boat is less than the river flow velocity . In such a case , boat cannot reach the point directly opposite to its starting point i.e., drift can never be zero , thus to minimize the drift boat start at an angle θ from normal direction up sterm as shown

Now again if we find the components of velocity of boat and perpendicular to the flow these are velocity along the river Vt=u−Vsinθ
and velocity perpendicular to the river ,Vy=vcosθ
time taken to cross the river is t=dvy=dcosθ
In this time drift x=(vA)t=(u−vsinθ)dvy=dvcosθ
in this time drift x=(vx)t=(u−Vsinθ)dvcosθ(or)x=udvsecθ−dtanθ
the drift x is minimum when dxdθ=0(or)(udv)(secθ,tanθ)−dsec2θ=0
(or)avsinθ=1(or)sinθ=vu=1n(asv=un)
so for minimum drift the boat must move at an angle θ=sin−1(vu) from normal direaction or an angle π2+sin−1(vu) from steam direction.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - LONG ANSWER TYPE QUESTIONS5videos
ELEMENTS OF VECTORS
- BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - SHORT ANSWER TYPE QUESTIONS10videos
ELEMENTS OF VECTORS
- BOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)5videos
ELECTROSTATICS
- BOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)10videos
GEOMETRICAL OPTICS
Similar Questions
A boat moves relative to water with a velocity v which is n times less than the river flow velocity u. At what angle to the stream direction must the boat move to minimize drifting ?
View SolutionA boat moves relative to water with a velocity v which is n times less than the river flow velocity u. At what angle to the stream direction must the boat move to minimize drifting ?
View SolutionA boat moves in still water with a velocity which is k times less than the river flow velocity. Find the angle to the stream direction at which the boat should be rowed to minimize drifting.
View SolutionA boat moves in still water with a velocity which is k times less than the river flow velocity. Find the angle to the stream direction at which the boat should be rowed to minimize drifting.
View SolutionA boat moves relative to water with a velocity which is 'n' times the river flow
a) If n<1 boat can not cross the river
b) If n = 1 boat can not cross the river without drifting
c) If n>1 boat can cross the river along shortest path
d) Boat can cross the river what ever is the value of n excluding zero valueView SolutionA swimmer capable of swimming with velocity v relative to water jumps in a flowing river having velocity u. The man swims a distance d down stream and returns back to the original position. Find out the time taken in complete motion.
View SolutionThe velocity of the water flowing from the inlet pipe is less than the velocity of water flowing out from the spin pipe B. Then
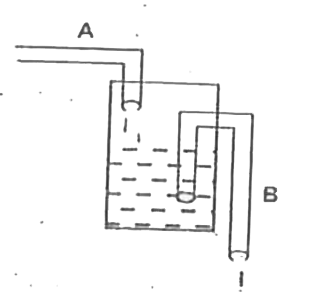 View Solution
View SolutionA boat crosses a river with a velocity of 8kmh. If the resulting velocity of boat is 10kmh then the velocity of river water is
View SolutionA river is flowing towards with a velocity of 5ms−1. The boat velocity is 10ms−1. The boat crosses the river by shortest path. Hence,
View SolutionA river is flowing towards with a velocity of 5ms−1. The boat velocity is 10ms−1. The boat crosses the river by shortest path. Hence,
View Solution
