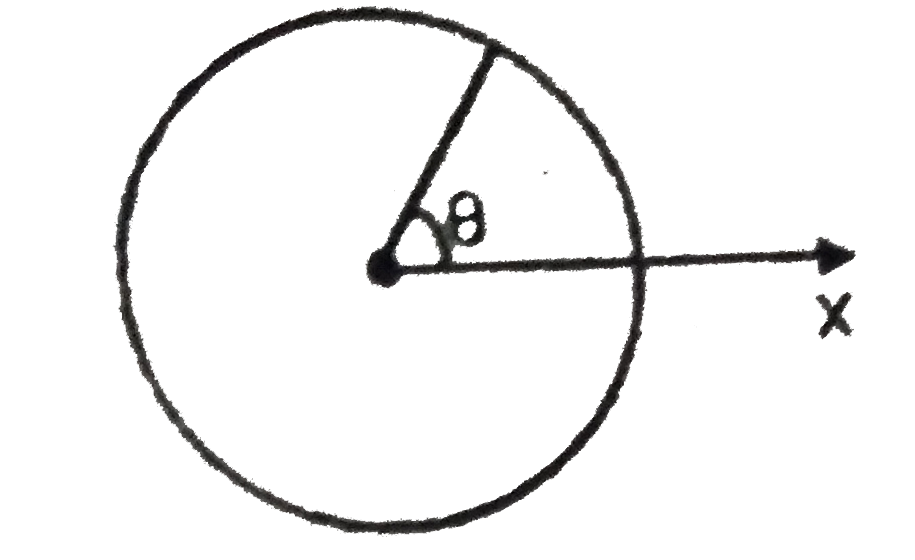
The linear charge density on a dielectric ring of radius R vanes with θ as λ=λ0cosθ/2, where λ0 is constant. Find the potential at the center O of the ring [in volt].
The correct Answer is:0
Step by step video & image solution for The linear charge density on a dielectric ring of radius R vanes with theta as lambda = lambda_0 cos theta//2, where lambda_0 is constant. Find the potential at the center O of the ring [in volt]. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) MATRIX MATCHING TYPE QUESTIONS)
1 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE
13 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
Similar Questions
The linear charge density on a ring of radius R is λ=λ0sin(θ) where λ0 is a constant and θ is angle of radius vector of any point on the ring with x-axis. The electric potential at centre of ring is
View SolutionA thin nonconducting ring of radius R has a linear charge density λ=λ0cosφ, where λ0 is a constant , ϕ is the azimuthal angle. Find the magnitude of the electric field strength
(a) at the centre of the ring ,
(b) on the axis of the ring as a function of the distance x from its centre. Investegation the obtained function at x>>R.
View Solutionthe linear charge density of a thin metallic rod varies with the distance x from the end as λ=λ0x2(0≤x≤l) The total charge on the rod is
View SolutionA ring of radius R carries a non - uniform charge of linear density λ=λ0cosθ sec in the figure) Magnitude of the net dipolement of the ring is :

View SolutionA half ring of radius r has a linear charge density λ.The potential at the centre of the half ring is
View SolutionLinear mass density of a rod AB(of≤n>h10m) varies with distance x from its end A as λ =λ0x3 (λ0 is positive constant) . Distance of centre of mass of the rod , from end B is
View SolutionLinear mass density of a rod AB ( of length 10 m) varied with distance x from its end A as λ=λ0x3 (λ0 is poitive constant). Distance of centre of mass the rod, form end B is
View SolutionThe given two fixed rings of radius R lie in XY plane as shown in the figure. Linear charge density of the rings A and B varies as per the relationλ=λ0sinθ and λ=λ0cosθ respectively where theta is measured from +x axis. Distance between the centre of the two rings is r>>R
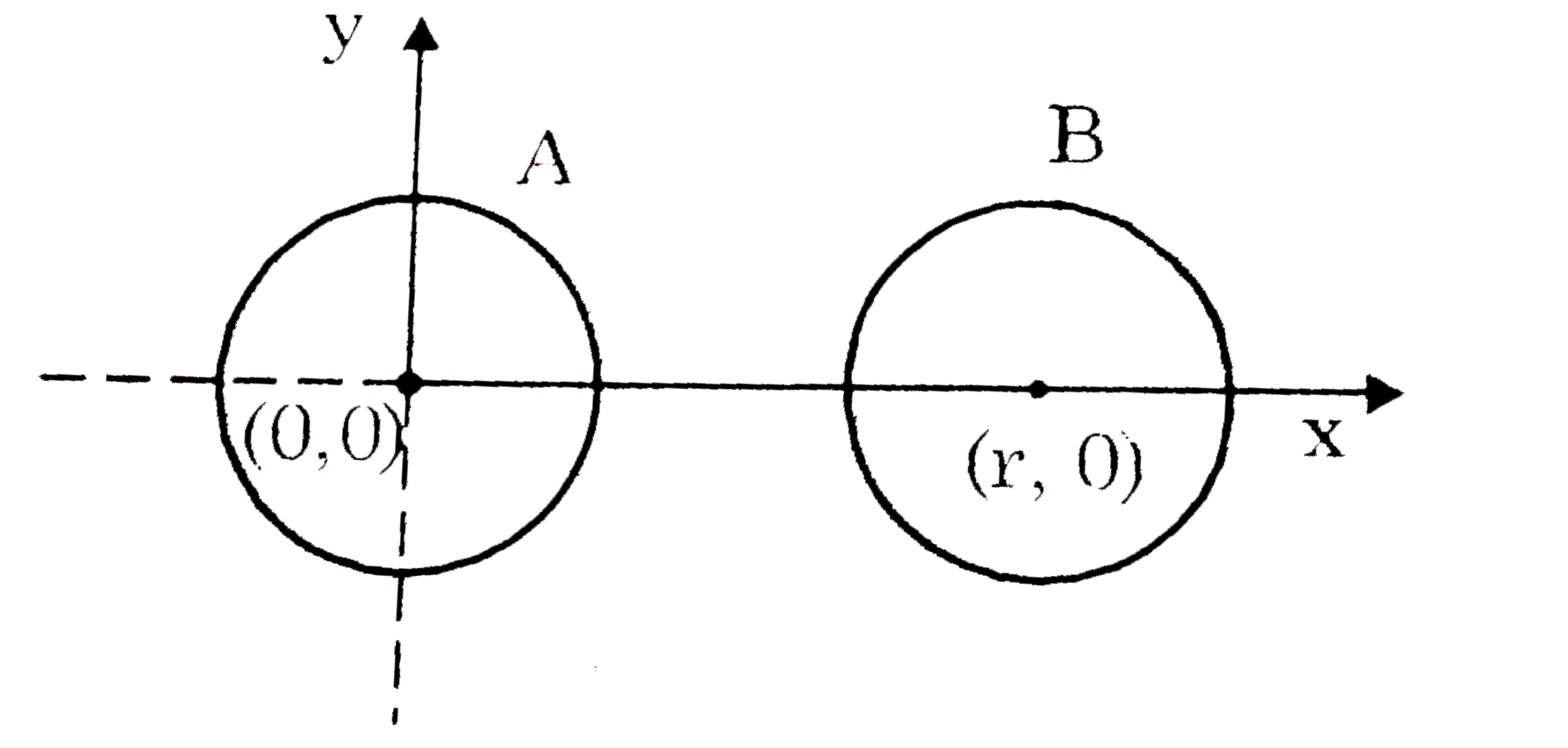
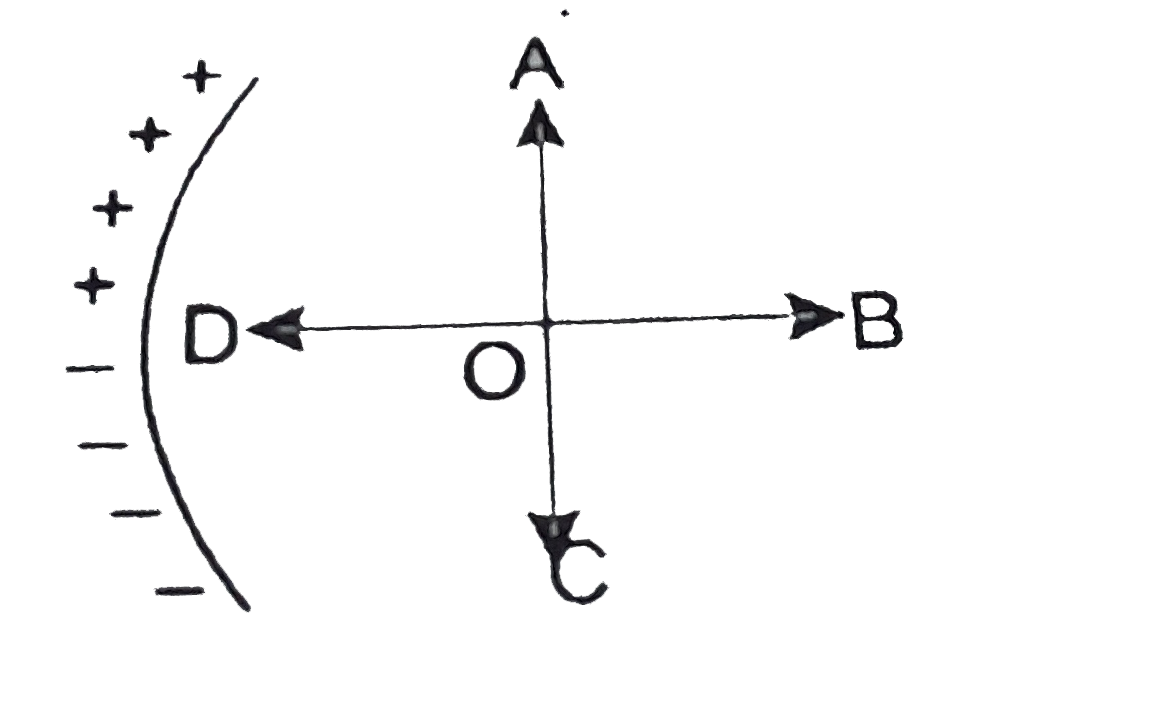
View SolutionThe linear charge density on upper half of semi-circular section of ring is λ and that at lower half is −λ. The direction of electric field at centre O of ring is :
View SolutionThe set of values of λ∈R such that tan2θ+secθ=λ holds for some θ is
View Solution
