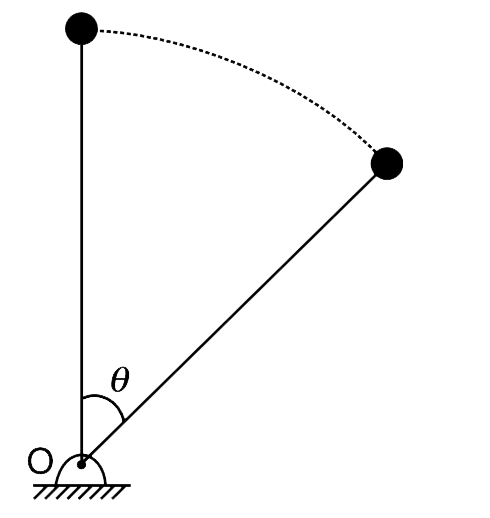
A bob of mass m attached to one end of a light rod hangs vertically. The rod is tuned throudh 90∘ so that it becomed horizontal and then relseased . Calculate the angle between the rod and vertical positior at which the tension in the rod is equal to weight of the bob.
As the rod moves from horizontal position OA to vertical position OB suppose T=mg at position P, where ∠BOP=θ figure
If υ velocity of bob at P then 12mυ2=mg(Lcosθ)
υ2=2gLcosθ …(i)
Net force acting on the bob along PO=T−mgcosθ
This must provide the necessary centripetal force
T−mgcosθ=mυ2L=mL(2gLcosθ) ... using (i)
=2mgcosθ
T=3mgcosθ
When T=mg,mg=3mgcosθ
cosθ=13=0.3333∴θ=cos−1(0.3333)=70∘30'

Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:PRADEEPChapter:WORK, ENERGY AND POWERExercise:value Based Question
Explore 5 Videos
- WORK, ENERGY AND POWERBook:PRADEEPChapter:WORK, ENERGY AND POWERExercise:Multiple choice question
Explore 29 Videos
- WORK, ENERGY AND POWERBook:PRADEEPChapter:WORK, ENERGY AND POWERExercise:Additional Exercises
Explore 3 Videos
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:Assertion- Reason Type Questions
Explore 19 Videos
Similar Questions
A rod of length L is hinged from one end. It is brought to horizontal position and released. The angular velocity of the rod when it is in vertical position. Is
View SolutionA light rigid rod has a bob of mass m attached to one of its end. The other end of the rod is pivoted so that the entire assembly can rotate freely in a vertical plane. Initially, the rod is held vertical as shown in the figure. From this position it is allowed to fall. (a) When the rod has rotated through θ=30∘ , what kind of force does it experience– compression or tension? (b) At what value of θ the compression (or tension) in the rod changes to tension (or compression)?
View Solution
Knowledge Check
In the figure shown, the cart of mass 6m is initially at rest. A particle of mass m is attached to the end of the light rod which can rotate freely about A. If the rod is released from rest in a horizontal position shown, determine the velocity vrel of the particle with respect to the cart when the rod is vertical. (Assume frictionless surface)
 A√73glB√76glC√143glD√83gl
A√73glB√76glC√143glD√83glA rod of length L is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod, when it is in vertical position, is
A√2gLB√3gLC√g2LD√gLA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]
A rod of mass m and length l is himged about one of its ends. The rod is released from horizontal position. When the rod becomes vertical, calculate (i) angular speed of the rod (ii) Hinge reaction.
View SolutionA uniform rod pivoted at its upper end hangs vertically. It is displaced through anangle of 60∘ and then released. Find the magnitude of the force acting on a particle of mass dm at the tip of the rod when the rod makes an angle of 37∘ with the vertical.
View SolutionAs shown in the figure, two blocks, each of mass m, suspended from the ends of a rigid light rod of length L. The rod is held horizontally on the fulcrum and then released.
(a) Find the initial angular acceleration of the rod.
(b) If the mass of rod is also m uniformly distributed. find the tension in the strings attached to blocks.

View SolutionA uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
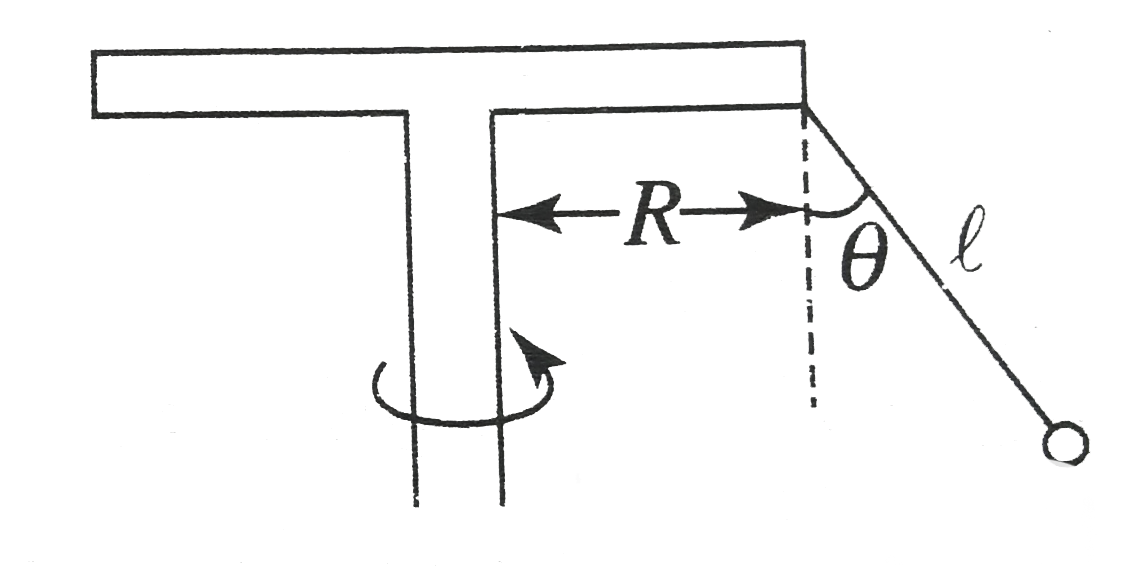
View SolutionA pendulum bob of mass m hangs from one end of a horizontal rod which is rotating about vertical axis with an unknown angular speed ω such that the light inextensible string of length l of the pedulum makes a constant angle θ with vertical. Find the
Q. tension in the string
View Solution