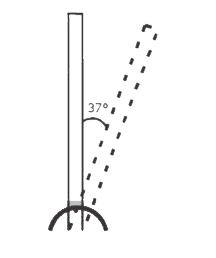
A uniform rod pivoted at its upper end hangs vertically. It is displaced through anangle of 60∘ and then released. Find the magnitude of the force acting on a particle of mass dm at the tip of the rod when the rod makes an angle of 37∘ with the vertical.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B, D

Let l=length of the rod and m=mass of the rod.
Applying energy principle
(12)Iω2≡mg12(cos370−cos600)
→12.(mω)23=mg12(45−12)t
→ω2=9g10l=0.9(gl)
Again mα=mg(1.2sin37∘)
=mg(1.2)×35
:>α=0.9(gl)
=anga––rae≤ration<br>So,→f∈douttheforceonthepartic≤atthetipoftherod<br>F_1=centrifugalforce<br>=(dm)omega^2l=0.9(dm)g<br>F_t=tan≥ntialforce<br>=(dm)alphal=0.9(dm)g<br>So total force ltbr> F=√F21+Ft2
=0.9√2(dm)g

Updated on:21/07/2023
|
Class 11PHYSICSRIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • A slender uniform rod of mass M and length l is pivoted at one ens so that it can rotate in a vertical plane, Fig. There is negligible friction at the pivot. The free end is held vertically above the pivot and then released. The angular acceleration of the rod when it makes an angle θ with the vertical is
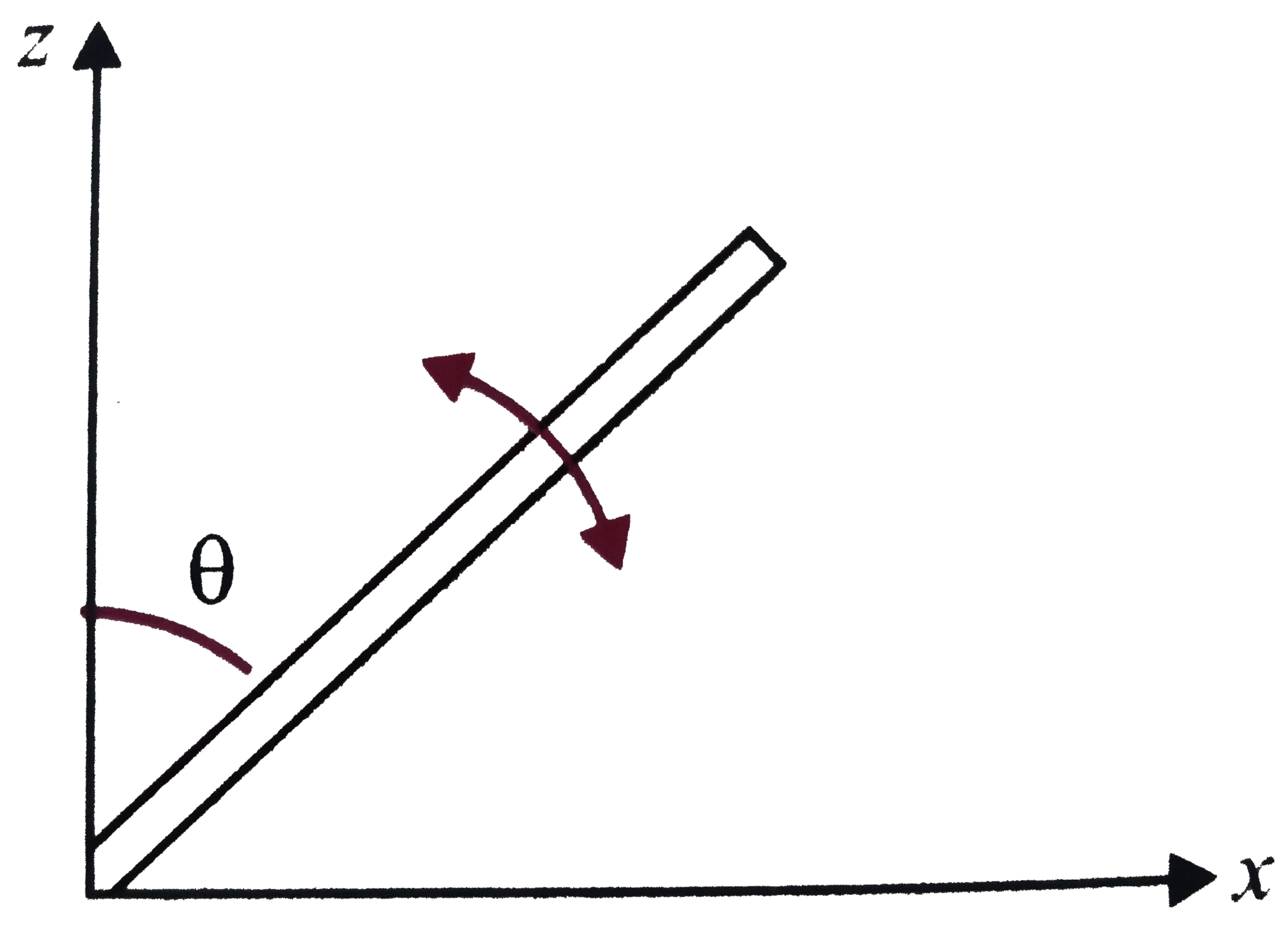    ocr_image

    A3g2lcosθ
    B2g3lcosθ
    C3g2lsinθ
    D2g3lsinθ

  • A uniform rod of length L pivoted at the bottom of a pond of depth L/2 stays in stable equilibrium as shown in the figure.
    ocr_image
    Find the force acting at the pivoted end of the rod in terms of mass m of the rod.

    A(√2−1)mg
    B(√2+1)mg
    C(√3+1)mg
    D(√2+3)mg

  • A uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is

    Asame at all points
    Bdifferent at differen points and maximum at centre of rod
    Cdifferent at different points and minimum at axis of rotation.
    Ddifferent at different points and maximum at axis of rotation