A body has maximum range R1 when projected up the plane. The same body when projected down the inclined plane, it has maximum range R2. Find the maximum horizontal range. Assume equal speed of projection in each case and the body is projected onto the inclined plane in the line of the greatest slope.
To solve the problem of finding the maximum horizontal range when a body is projected up and down an inclined plane, we can follow these steps:
1. Understanding the Problem:
We have a body projected on an inclined plane at an angle θ with the horizontal. We denote the maximum range when projected up the plane as R1 and when projected down the plane as R2. We need to find the maximum horizontal range R.
2. Formulas for Maximum Range:
- For projection up the inclined plane:
R1=v2g(1+sinθ)
- For projection down the inclined plane:
R2=v2g(1−sinθ)
3. Expressing the Horizontal Range:
The maximum horizontal range R can be expressed using the same initial speed v and the angle of projection. The formula for maximum horizontal range on a flat surface (when θ = 0) is:
R=v2g
4. Relating R1 and R2:
From the equations for R1 and R2, we can express sinθ in terms of R1 and R2:
- From R1:
sinθ=R1g/v2−11
- From R2:
sinθ=1−R2g/v21
5. Equating the Two Expressions:
Set the two expressions for sinθ equal to each other:
R1g/v2−11=1−R2g/v21
6. Solving for R:
Rearranging and simplifying the equation leads to:
1R1+1R2=2R
Therefore, we can express R as:
R=2R1R2R1+R2
Final Result:
The maximum horizontal range R is given by:
R=2R1R2R1+R2
We have a body projected on an inclined plane at an angle θ with the horizontal. We denote the maximum range when projected up the plane as R1 and when projected down the plane as R2. We need to find the maximum horizontal range R.
- For projection up the inclined plane:
R1=v2g(1+sinθ)
- For projection down the inclined plane:
R2=v2g(1−sinθ)
The maximum horizontal range R can be expressed using the same initial speed v and the angle of projection. The formula for maximum horizontal range on a flat surface (when θ = 0) is:
R=v2g
From the equations for R1 and R2, we can express sinθ in terms of R1 and R2:
- From R1:
sinθ=R1g/v2−11
- From R2:
sinθ=1−R2g/v21
Set the two expressions for sinθ equal to each other:
R1g/v2−11=1−R2g/v21
Rearranging and simplifying the equation leads to:
1R1+1R2=2R
Therefore, we can express R as:
R=2R1R2R1+R2
The maximum horizontal range R is given by:
R=2R1R2R1+R2
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Solved Examples
7 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.1
15 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
Knowledge Check
A body has maximum range R1 when projected up the inclined plane. The same body when projected down, the inclined plane. It has maximum range R2. Find its maximum horizontal range. Assume the equal speed of projection in each case and the body is projected onto the gretest slope.
 AR=2R1R2R1−R2BR=2R1R2R1+R2CR=R1R2R1−R2DR=4R1R2R1+R2
AR=2R1R2R1−R2BR=2R1R2R1+R2CR=R1R2R1−R2DR=4R1R2R1+R2If R is the range of a projectiel on a horizontal plane and h its maximum height, the maximum horizontal range with the same velocity of projection is:
A2hBR28hC2R+h28RD2h+R28hThe horizontal range and the maximum height of a projectile are equal. The angle of projection of the projectile is
Aθ=tan−1(14)Bθ=tan−1(4)Cθ=tan−1(2)Dθ=45∘
A projectile when fired at a certain inclination has maximum rang R. Find its maximum height attained by it in terms of R .
View SolutionFor a projectile projected at an angle _____the maximum height and horizontal range are equal.
View SolutionFor a given velocity of projection from a point on the inclined plane, the maximum range down the plane is three times the maximum range up the incline. Then find the angle of inclination of the inclined plane.
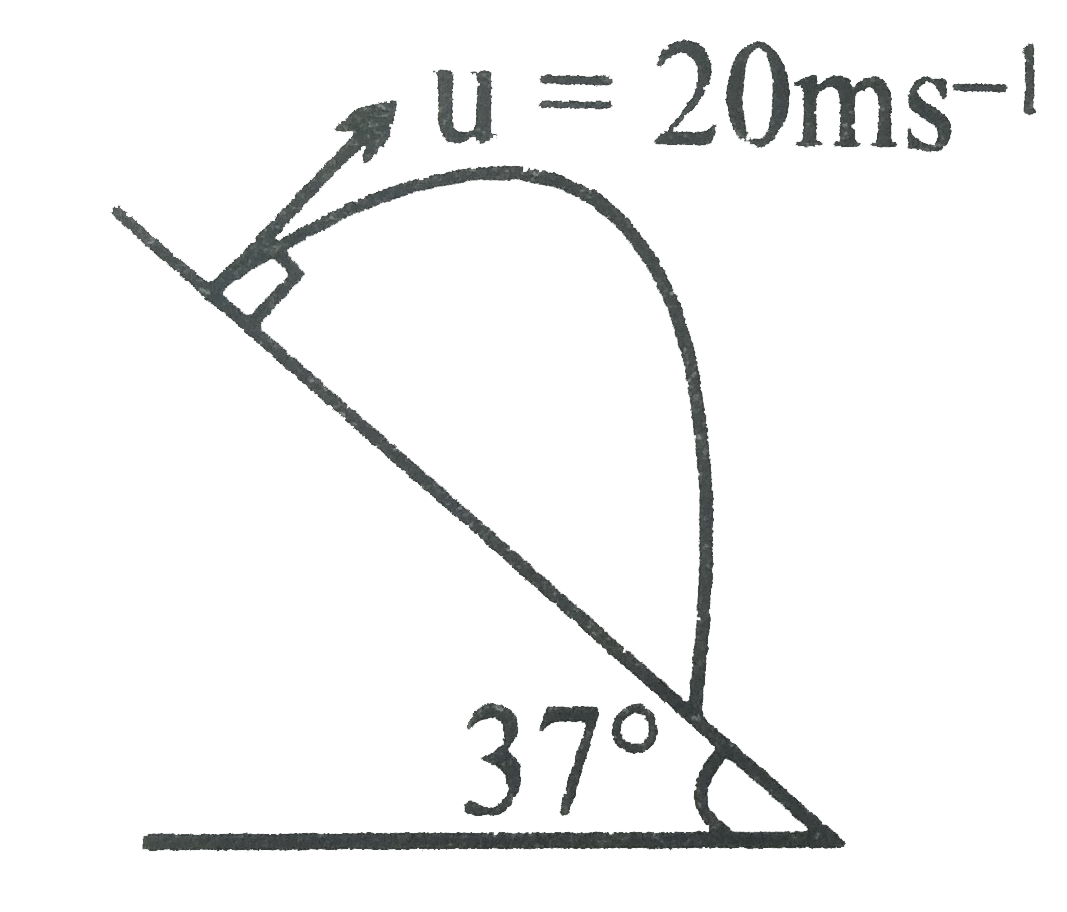
View SolutionFind range of projectile on the inclined plane which is projected perpendicular to the incline plane with velcoity 20m/s as shwon in figure.
View SolutionA body is projected with velocity u so that its horizontal range is twice the maximum height.The range is
View Solution
