A body is in contact with the vertical front part of the truck. The coefficient of friction between the body and the truck is μ. The minimum acceleration with which the truck should travel so that the body does not fall down is
μ/g
μg
g/μ
μ2g
The correct Answer is:C
To solve the problem, we need to analyze the forces acting on the body in contact with the vertical front part of the truck. The goal is to find the minimum acceleration of the truck such that the body does not fall down due to gravity.
1. Identify the Forces Acting on the Body:
- The weight of the body acts downward and is given by W=mg, where m is the mass of the body and g is the acceleration due to gravity.
- The normal force N acts perpendicular to the surface of contact (which is vertical in this case).
- The frictional force f acts upward, opposing the weight of the body. The maximum static frictional force can be expressed as f=μN, where μ is the coefficient of friction.
2. Set Up the Equations:
- For the body to remain in contact with the truck and not fall, the upward frictional force must balance the downward weight of the body. Thus, we have:
f=mg
- Substituting the expression for friction, we get:
μN=mg
3. Relate Normal Force to Truck's Acceleration:
- The normal force N is equal to the net force required to accelerate the body with the truck. If the truck accelerates with an acceleration a, then the net force acting on the body in the horizontal direction is given by:
N=ma
- Therefore, we can substitute N in the friction equation:
μ(ma)=mg
4. Solve for Truck's Acceleration:
- Rearranging the equation gives:
a=gμ
Final Answer:
The minimum acceleration with which the truck should travel so that the body does not fall down is:
a=gμ
- The weight of the body acts downward and is given by W=mg, where m is the mass of the body and g is the acceleration due to gravity.
- The normal force N acts perpendicular to the surface of contact (which is vertical in this case).
- The frictional force f acts upward, opposing the weight of the body. The maximum static frictional force can be expressed as f=μN, where μ is the coefficient of friction.
- For the body to remain in contact with the truck and not fall, the upward frictional force must balance the downward weight of the body. Thus, we have:
f=mg
- Substituting the expression for friction, we get:
μN=mg
- The normal force N is equal to the net force required to accelerate the body with the truck. If the truck accelerates with an acceleration a, then the net force acting on the body in the horizontal direction is given by:
N=ma
- Therefore, we can substitute N in the friction equation:
μ(ma)=mg
- Rearranging the equation gives:
a=gμ
The minimum acceleration with which the truck should travel so that the body does not fall down is:
a=gμ
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - II
136 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
10 Videos
Similar Questions
A cart of mass M has a block of mass m in contact with it as shown in the figure-2.133. The coefficient of friction between the block and the cart is μ. What is the minimum acceleration of the cart so that the block m does not fall ?

View SolutionA body is pushed against vertical wall as shown. If the coefficient of friction between the body and the wall is 0.5, the magnitude of acceleration of the block is 10 K. Where K is
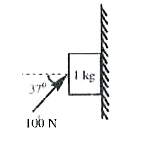
View Solution
Knowledge Check
A block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
A10NB5NC2.5ND20N
If angle of repose is ϕ, the coefficient of static friction between body and the plane is
View Solution
Consider the figure shown here of a moving cart C. if the coefficient of friction between the block A and the cart is μ, then calculate the minimum acceleration a of the cart C so that the block A does not fall.
View SolutionA block of mass m is in contact with the cart C as shown in The coefficient of static friction between the block and the cart is μ The acceleration a of the cart that will prevent the block from falling satisfies
 .
.
View SolutionA body moves along a circular path of radius 5m. The coefficient of friction between the surface of the path and the body is 0.5. The angular velocity in rad/s with which the body should move so that it does not leave the path is (g−10m/s−2)
View SolutionCoefficient of friction between A and B is μ . The minimum force F with which A will be pushed such that B will not slip down is -
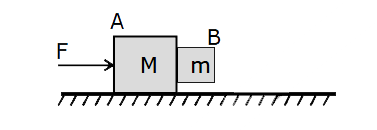
View SolutionA block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
View SolutionA block of mass m sides down an inclined right angled trough .If the coefficient of friction between block and the trough is μk acceleration of the block down the plane is

View Solution
