A body is projected vartically upwards from the bottom of a crater of moon of depth $\frac{R}{100}$ where R is the radius of moon with a velocity equal to the escape velocity on the surface of moon. Calculate maximum height attained by the body formt eh surface of the moon.

Video Solution

Text Solution

Verified by Experts

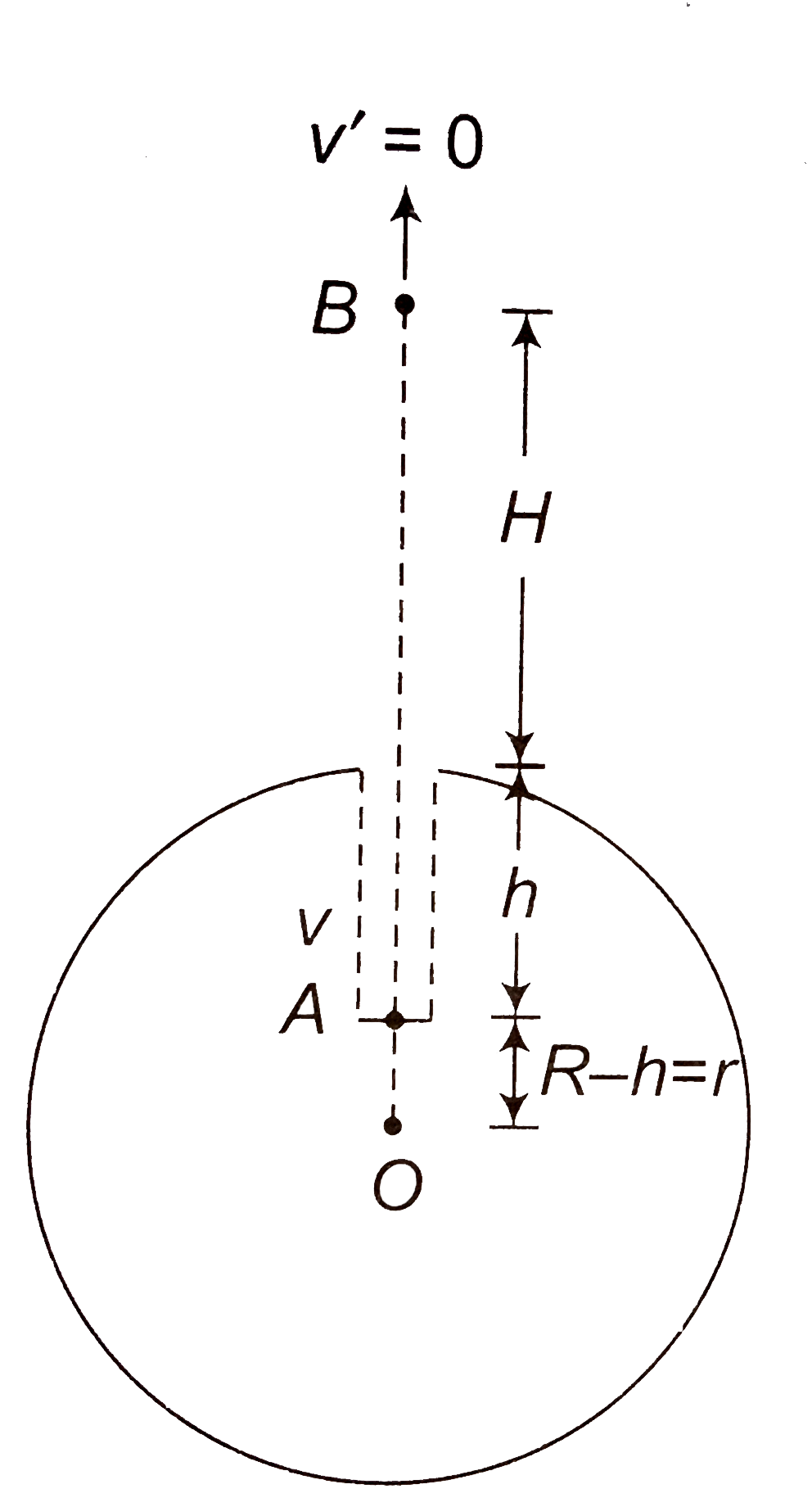
Gravitational potential inside solid sphere at distance $r$ from centre.
$V = - \frac{G M (3 R^{2} - r^{2})}{2 R^{3}}$
$r = R - \frac{R}{100} = \frac{99 R}{100}$
Projection velocity at $A, v = \sqrt{\frac{2 G M}{R}}$
Applying energy conservation between $A$ and $B$
$K_{A} + U_{A} = K_{B} + U_{B}$
$K_{A} + m V_{A} = K_{B} + V_{B}$
$V_{A} = - \frac{G M [3 R^{2} - {(\frac{99 R}{100})}^{2}]}{2 R^{3}} = \frac{- G M R^{2}}{2 R^{3}} [3 - {(0.99)}^{2}]$
$= - \frac{G M}{2 R} [3 - {(1 - 0.01)}^{2}] = - \frac{G M}{2 R} [3 - (1 - 0.02)]$
$= - \frac{1.01 G M}{R}$
$v_{B} = - \frac{G M}{(R + H)}$
$K_{A} = \frac{1}{2} m v^{2} = \frac{1}{2} . \frac{2 G M m}{R} = \frac{G M m}{R}$
$K_{B} = 0$
$\frac{G M m}{R} - \frac{1.01 G M}{R} = 0 - \frac{G M}{(R + H)}$
$- 0.01 = - \frac{1}{1 + \frac{H}{R}}$
$1 + \frac{H}{R} = 100 \Rightarrow H = 99 R$

Updated on:21/07/2023