The weight of an object in the coal mine, sea level and at the top of the mountain are W1,W2 and W3 respectively, then
W2>W1>W3
W1=W2=W3
W1<W2<W3
W1>W2>W3
The correct Answer is:A
To solve the problem regarding the weights of an object at different locations (coal mine, sea level, and top of a mountain), we will analyze how the gravitational force (weight) changes based on the distance from the center of the Earth.
1. Understanding Weight:
The weight of an object is given by the formula:
W=m⋅g
where m is the mass of the object and g is the acceleration due to gravity.
2. Weight at Sea Level (W2):
At sea level, the weight is simply:
W2=m⋅g
Here, g is the standard acceleration due to gravity at sea level.
3. Weight in the Coal Mine (W1):
When we go down into a coal mine, we are moving below the surface of the Earth. The variation of gravitational acceleration at a depth d is given by:
g′=g(1−dR)
where R is the radius of the Earth. Thus, the weight at this depth is:
W1=m⋅g′=m⋅g(1−dR)
4. Weight at the Top of the Mountain (W3):
When we go to a height h above sea level, the variation of gravitational acceleration is given by:
g′=g(1−2hR)
Therefore, the weight at this height is:
W3=m⋅g′=m⋅g(1−2hR)
5. Comparing Weights:
Now we need to compare W1, W2, and W3:
- At sea level, W2=m⋅g.
- In the coal mine, W1=m⋅g(1−dR) which is less than W2 since d/R is positive.
- At the top of the mountain, W3=m⋅g(1−2hR) which is also less than W2 and generally less than W1 if h is sufficiently large.
6. Conclusion:
From the analysis, we can conclude:
W2>W1>W3
Therefore, the relationship between the weights is:
W2>W1>W3
Final Answer:
The correct relationship is W2>W1>W3.
---
The weight of an object is given by the formula:
W=m⋅g
where m is the mass of the object and g is the acceleration due to gravity.
At sea level, the weight is simply:
W2=m⋅g
Here, g is the standard acceleration due to gravity at sea level.
When we go down into a coal mine, we are moving below the surface of the Earth. The variation of gravitational acceleration at a depth d is given by:
g′=g(1−dR)
where R is the radius of the Earth. Thus, the weight at this depth is:
W1=m⋅g′=m⋅g(1−dR)
When we go to a height h above sea level, the variation of gravitational acceleration is given by:
g′=g(1−2hR)
Therefore, the weight at this height is:
W3=m⋅g′=m⋅g(1−2hR)
Now we need to compare W1, W2, and W3:
- At sea level, W2=m⋅g.
- In the coal mine, W1=m⋅g(1−dR) which is less than W2 since d/R is positive.
- At the top of the mountain, W3=m⋅g(1−2hR) which is also less than W2 and generally less than W1 if h is sufficiently large.
From the analysis, we can conclude:
W2>W1>W3
Therefore, the relationship between the weights is:
W2>W1>W3
The correct relationship is W2>W1>W3.
Topper's Solved these Questions
Similar Questions
The work done in moving a particle in the gravitational field of earth from point A to point B along three different paths 1,2 and 3 are W1,W2 and W3 respectively , then
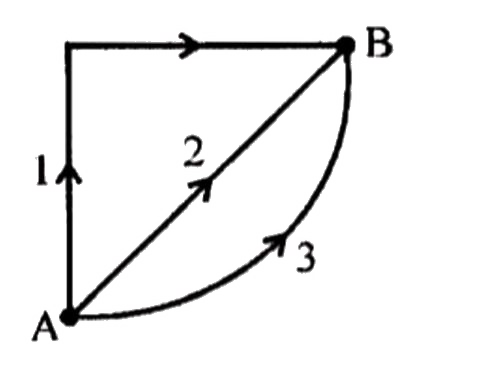
View Solution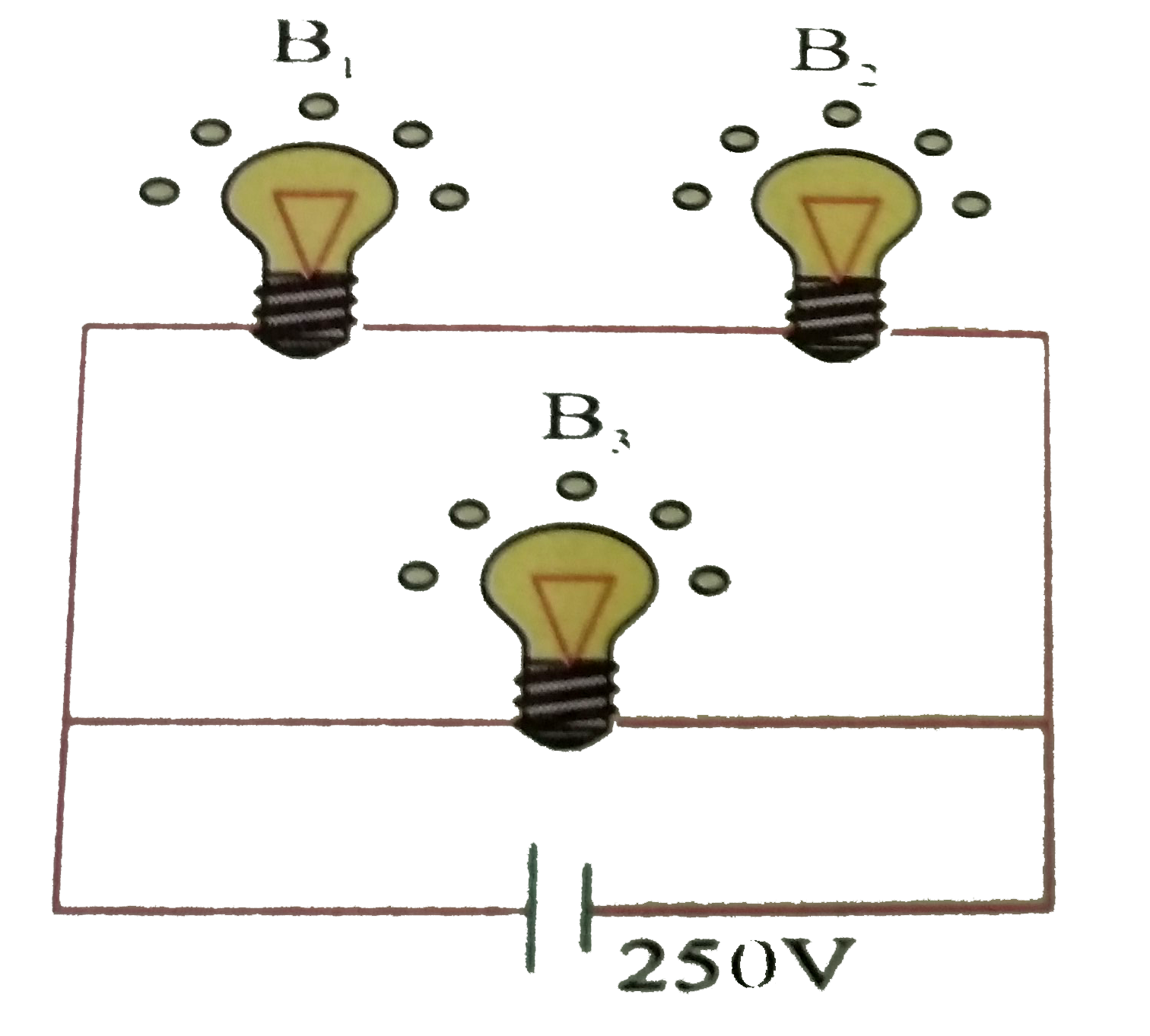
A 100 W bulb B1 and two 60 W bulbs B2 and B3, are connected to a 250V source, as shown in the figure now W1,W2 and W3 are the output powers of the bulbs B1,B2 and B3 respectively then
View Solution
Knowledge Check
W1,W2 and W3 are the different sizes of windows 1,2, and 3 respectively placed in a vertical plane. A particle is thrown up in the vertical plane. Let t1,t2 and t3 are the time taken to cross the window W1,W2 and W3 respectively and ΔV1,ΔV2 and ΔV3 are the change in speed after respective window cross.
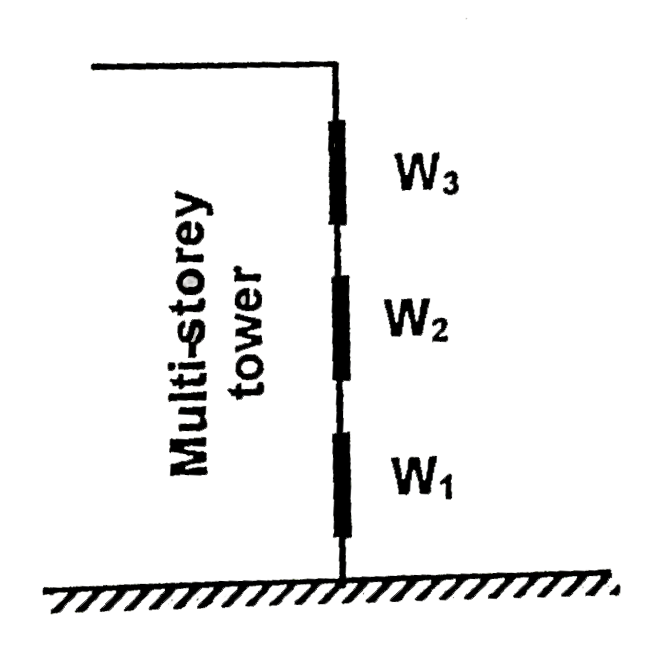 AAverage speed of the particle passing the windows may be equal if W1<W2<W3BAverage speed of the particle passing the windows may be equal if W1>W2>W3CIf W1=W2=WP3, the change in speed of the particle while crossing the windows will satisfy ΔV1<ΔV2<ΔV3DIf W1=W2=W3, the time taken by particle to cross the windows will satisfy t1<t2<t3
AAverage speed of the particle passing the windows may be equal if W1<W2<W3BAverage speed of the particle passing the windows may be equal if W1>W2>W3CIf W1=W2=WP3, the change in speed of the particle while crossing the windows will satisfy ΔV1<ΔV2<ΔV3DIf W1=W2=W3, the time taken by particle to cross the windows will satisfy t1<t2<t3A given mass of a gas expands from the state A to the state B by three paths 1,2 and 3 as shown in the figure, If W1,W2 and W3 respectively be the work done by the gas along the three paths then
 AW1>W2>W3BW1<W2<W3CW1=W2=W3DW1<W2=W3
AW1>W2>W3BW1<W2<W3CW1=W2=W3DW1<W2=W3A given mass of gas expands from state A to state B by three paths 1, 2 and 3 as shown in the figure
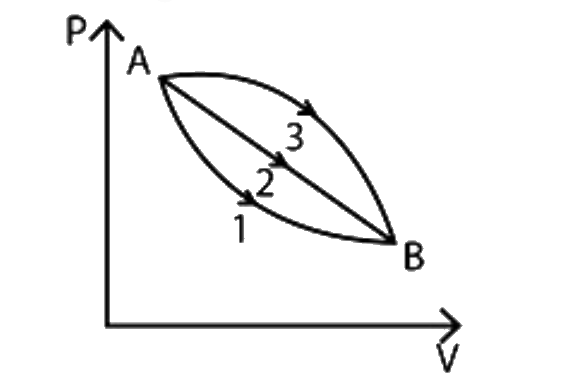
If w1,w2andw3 respectively are be the works done by the gas along three paths, thenAw1>w2>w3Bw1<w2<w3Cw1=w2=w3Dw2<w3<w1
Why it is cooler at the top of a mountain than at sea level?
View SolutionA given mass of gas expands from state A to state B by three paths 1, 2 and 3 as shown in the figure

If w1,w2andw3 respectively are be the works done by the gas along three paths, then
View SolutionIf W1andW2 are the weights of two reactants in any reaction, having their equivalent weights E1andE2 respectively, which of the following equations represents the law of equivalence correctly?
(a) W1E1=W2E2 (b) W1E2=W2E1 ( c ) W1W2=E1E2
View SolutionGiven T-p curve for three processes. Work done in process 1, 2 and 3 (if initial and final pressure are same for all processes) is W1,W2 and W3 respectively. Correct order is

View SolutionA n object is weighed at the North Pole by a beam balance and a spring balance, giving reading of WB and WS respectively. It is again weighed in the same manner at the equator, giving readings of WB' and WS' respectively. Assume that the acceleration due to gravity is the same everywhere and that the balances are sensitive.
View Solution