A body is projected vertically upward from the surface of the earth with escape velocity. Calculate the time in which it will be at a height (measured from the surface of the arth) 8 time the radius of the earth (R). Acceleration due to gravity on the surface of the earth is g.
The correct Answer is:t=523√R2g
To solve the problem, we need to calculate the time taken for a body projected vertically upward from the surface of the Earth with escape velocity to reach a height of 8 times the radius of the Earth (8R). The acceleration due to gravity at the surface of the Earth is denoted as g.
1. Understanding Escape Velocity:
The escape velocity (ve) from the surface of the Earth is given by the formula:
ve=√2GMR
where G is the gravitational constant, M is the mass of the Earth, and R is the radius of the Earth.
2. Energy Conservation:
When the body is projected with escape velocity, the total mechanical energy at the surface is zero:
12mv2e−GMmR=0
This implies that the kinetic energy equals the gravitational potential energy at the surface.
3. Velocity at Height x:
At a distance x from the center of the Earth, the velocity V of the body can be expressed as:
12mV2−GMmx=0
Rearranging gives:
V=√2GMx
4. Relating Velocity and Time:
The velocity can also be expressed as:
V=dxdt
Therefore, we have:
√2GMx=dxdt
Rearranging gives:
dt=dx√2GMx=√x2GMdx
5. Integrating to Find Time:
To find the time taken to reach a height of 8R (which corresponds to a distance of 9R from the center of the Earth), we need to integrate from R to 9R:
t=∫9RR√x2GMdx
The integral simplifies to:
t=√12GM∫9RR√xdx
6. Calculating the Integral:
The integral ∫√xdx=23x3/2. Evaluating from R to 9R:
∫9RR√xdx=(23x3/2)9RR=23((9R)3/2−R3/2)
Simplifying gives:
=23(27R3/2−R3/2)=23⋅26R3/2=523R3/2
7. Final Expression for Time:
Substituting back into the expression for t:
t=√12GM⋅523R3/2
We know that GMR2=g, so:
t=523√R2g
Final Answer:
The time taken for the body to reach a height of 8R from the surface of the Earth is:
t=523√R2g
The escape velocity (ve) from the surface of the Earth is given by the formula:
ve=√2GMR
where G is the gravitational constant, M is the mass of the Earth, and R is the radius of the Earth.
When the body is projected with escape velocity, the total mechanical energy at the surface is zero:
12mv2e−GMmR=0
This implies that the kinetic energy equals the gravitational potential energy at the surface.
At a distance x from the center of the Earth, the velocity V of the body can be expressed as:
12mV2−GMmx=0
Rearranging gives:
V=√2GMx
The velocity can also be expressed as:
V=dxdt
Therefore, we have:
√2GMx=dxdt
Rearranging gives:
dt=dx√2GMx=√x2GMdx
To find the time taken to reach a height of 8R (which corresponds to a distance of 9R from the center of the Earth), we need to integrate from R to 9R:
t=∫9RR√x2GMdx
The integral simplifies to:
t=√12GM∫9RR√xdx
The integral ∫√xdx=23x3/2. Evaluating from R to 9R:
∫9RR√xdx=(23x3/2)9RR=23((9R)3/2−R3/2)
Simplifying gives:
=23(27R3/2−R3/2)=23⋅26R3/2=523R3/2
Substituting back into the expression for t:
t=√12GM⋅523R3/2
We know that GMR2=g, so:
t=523√R2g
The time taken for the body to reach a height of 8R from the surface of the Earth is:
t=523√R2g
Topper's Solved these Questions
Similar Questions
A body is projected vertically upward from the surface of earth with a velocity sufficient to carry it to initially. Calculate the time taken by it to reach height h.
View SolutionCalculate the distance from the surface of the earth at which above the surface, acceleration due to gravity is the same as below the earth
View Solution
Knowledge Check
A body is projected vertically upward from the surface of the earth, then the velocity-time graph is:-
A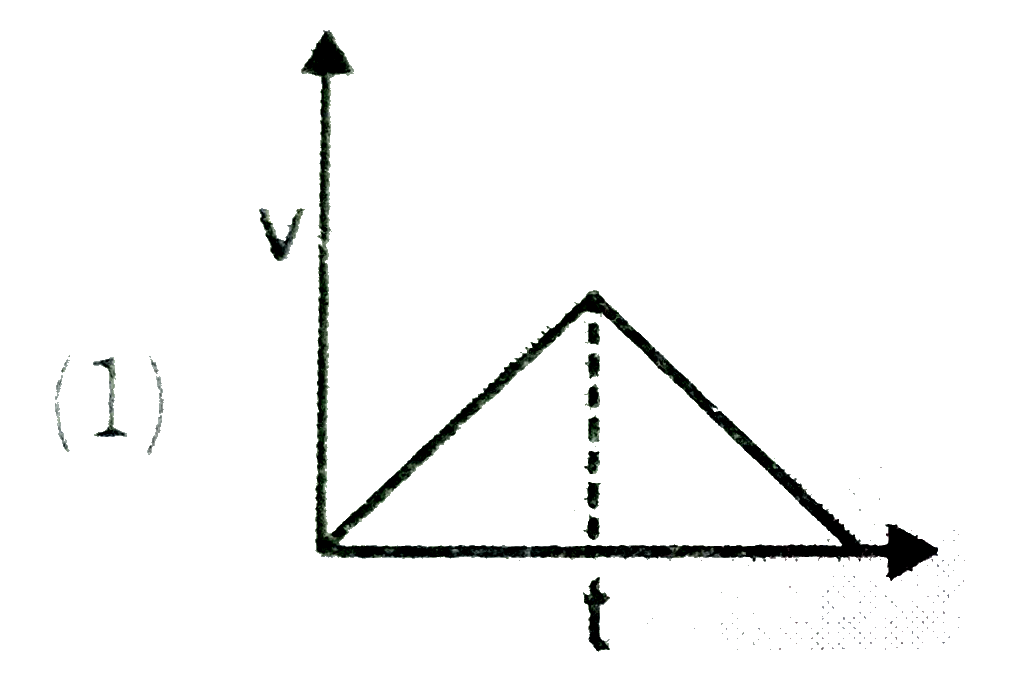 B
B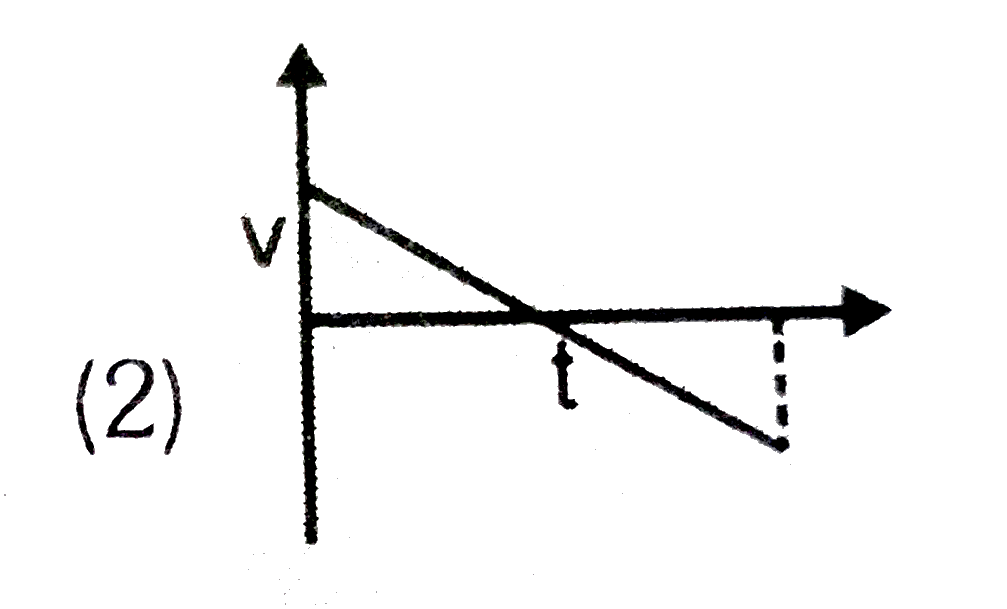 C
C D
D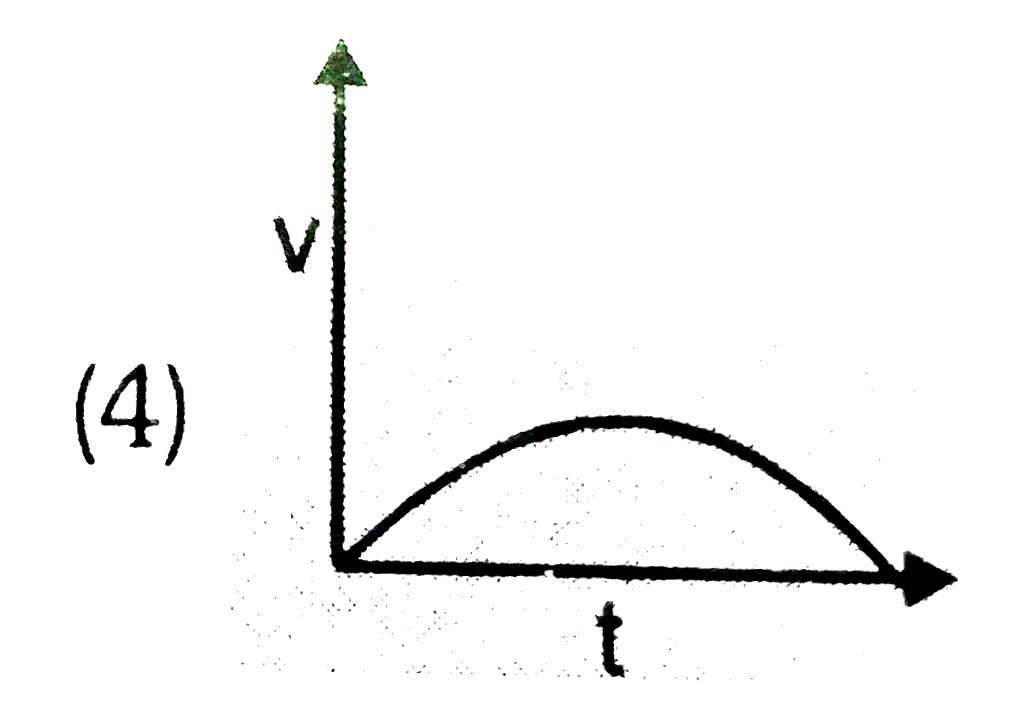
A body is projected vertically up from surface of the earth with a velocity half of escape velocity. The ratio of its maximum height of ascent and radius of earth is
A1:1B1:2C1:3D1:4If R is the radius of the earth and g the acceleration due to gravity on the earth’s surface, the mean density of the earth is
A4πG/3gRB3πR/4gGC3g/4πRGDπRg/12G
A particle of mass 'm' is raised to a height h=R from the surface of earth. Find increase in potential energy. R= radius of earth. g= acceleration due to gravity on the surface of earth.
View SolutionA body is projected vertically upwards from the surface of the earth with a velocity equal to half of escape velocity of the earth. If R is radius of the earth, maximum height attained by the body from the surface of the earth is
View SolutionThe escape velocity from the surface of the earth is (where RE is the radius of the earth )
View SolutionA body is thrown from the surface of the earth with velocity u m/s. The maximum height in metre above the surface of the earth up to which it will reach is (where, R = radish of earth, g=acceleration due to gravity)
View SolutionWhat will be the acceleration due to gravity at height h if h gt gt R . Where R is radius of earth and g is acceleration due to gravity on the surface of earth
View Solution
