A body is projected vertically upwards from the earth's surface. The body reaches a height equal to one half of radius of earth. Calculate the initial speed with which the body was projected initially.
Radius of earth = 6,400 km
Mass of earth =6×1024kg
The correct Answer is:6.45 km/s
To solve the problem of calculating the initial speed with which a body is projected vertically upwards from the Earth's surface, we can use the principle of conservation of energy. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Problem
A body is projected upwards and reaches a height equal to half the radius of the Earth. We need to find the initial speed (V) of the body.
Step 2: Define the Variables
- Let R be the radius of the Earth, which is given as 6400km=6400×103m.
- Let M be the mass of the Earth, given as 6×1024kg.
- Let g be the gravitational constant, approximately 6.67×10−11N m2/kg2.
Step 3: Apply Conservation of Energy
The total mechanical energy at the surface of the Earth (initial state) must equal the total mechanical energy at the maximum height (final state).
1. Initial Energy (at the surface):
- Kinetic Energy (KE) = 12mV2
- Potential Energy (PE) = −GMmR
Therefore, the total initial energy E1 is:
E1=12mV2−GMmR
2. Final Energy (at height h=R2):
- At maximum height, the kinetic energy is zero (the body momentarily stops).
- The potential energy at height h is:
PE=−GMmR+h=−GMmR+R2=−GMm3R2=−2GMm3R
Therefore, the total final energy E2 is:
E2=0−2GMm3R
Step 4: Set Up the Energy Conservation Equation
Since energy is conserved:
E1=E2
Substituting the expressions for E1 and E2:
12mV2−GMmR=−2GMm3R
Step 5: Simplify the Equation
1. Cancel m from both sides (assuming m≠0):
12V2−GMR=−2GM3R
2. Rearranging gives:
12V2=GMR−2GM3R
3. Combine the terms on the right:
12V2=3GM3R−2GM3R=GM3R
Step 6: Solve for V
Multiply both sides by 2:
V2=2GM3R
Taking the square root:
V=√2GM3R
Step 7: Substitute Known Values
Substituting G=6.67×10−11N m2/kg2, M=6×1024kg, and R=6400×103m:
V=
⎷2×(6.67×10−11)×(6×1024)3×(6400×103)
Calculating this gives:
V≈6456.6m/s≈6.45km/s
Final Answer
The initial speed with which the body was projected is approximately 6.45 km/s.
---
A body is projected upwards and reaches a height equal to half the radius of the Earth. We need to find the initial speed (V) of the body.
- Let R be the radius of the Earth, which is given as 6400km=6400×103m.
- Let M be the mass of the Earth, given as 6×1024kg.
- Let g be the gravitational constant, approximately 6.67×10−11N m2/kg2.
The total mechanical energy at the surface of the Earth (initial state) must equal the total mechanical energy at the maximum height (final state).
- Kinetic Energy (KE) = 12mV2
- Potential Energy (PE) = −GMmR
E1=12mV2−GMmR
- At maximum height, the kinetic energy is zero (the body momentarily stops).
- The potential energy at height h is:
PE=−GMmR+h=−GMmR+R2=−GMm3R2=−2GMm3R
E2=0−2GMm3R
Since energy is conserved:
E1=E2
Substituting the expressions for E1 and E2:
12mV2−GMmR=−2GMm3R
1. Cancel m from both sides (assuming m≠0):
12V2−GMR=−2GM3R
12V2=GMR−2GM3R
12V2=3GM3R−2GM3R=GM3R
Multiply both sides by 2:
V2=2GM3R
Taking the square root:
V=√2GM3R
Substituting G=6.67×10−11N m2/kg2, M=6×1024kg, and R=6400×103m:
V=
⎷2×(6.67×10−11)×(6×1024)3×(6400×103)
V≈6456.6m/s≈6.45km/s
The initial speed with which the body was projected is approximately 6.45 km/s.
Topper's Solved these Questions
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Conceptual Questions
19 Videos
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Tough & Tricky Problems
10 Videos
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Chapter Practice Test
15 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
Similar Questions
A body is projected vertically upwards from the surface of the Earth so as to reach a height equal to the radius of the Earth. Neglecting resistance due to it, calculate the initial speed which should be imparted to the body. Mass of Earth =5.98×1024kg, Radius of Earth =6400km, G=6.67×10−11Nm2kg−2.
View SolutionA body is projected vertically upward from the surface of earth with a velocity sufficient to carry it to initially. Calculate the time taken by it to reach height h.
View Solution
Knowledge Check
If a body is to be projected vertically upwards from earth's surface to reach a height of 10R where R is the radius of earth. The velocity required to be si is
A√2411grB√2211grC√2011grD√1811grA body is projected vertically upward from the surface of the earth, then the velocity-time graph is:-
A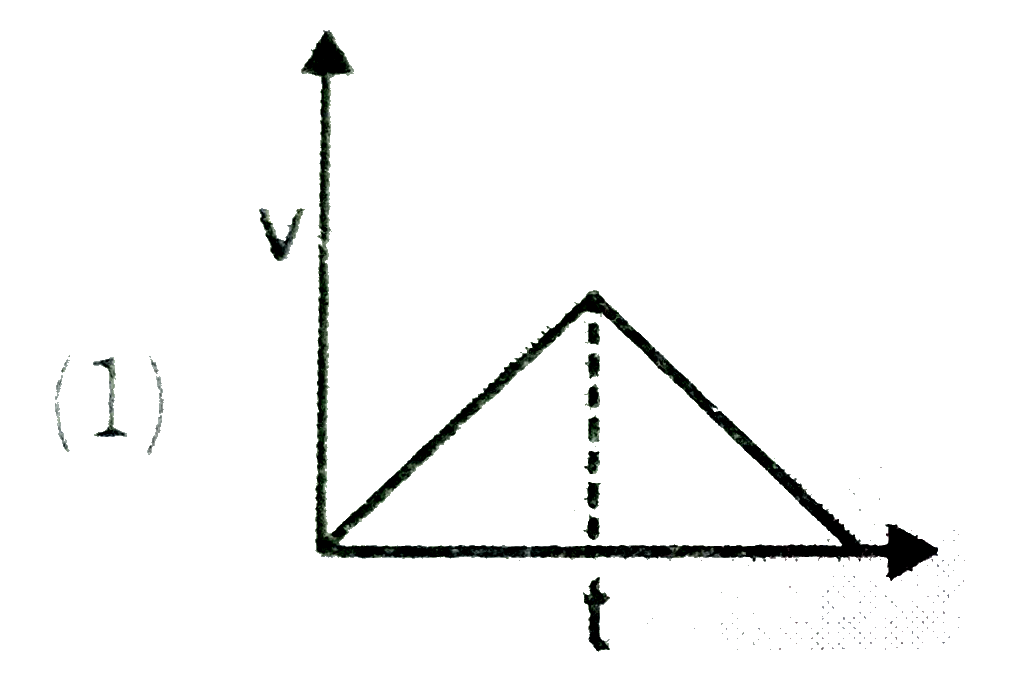 B
B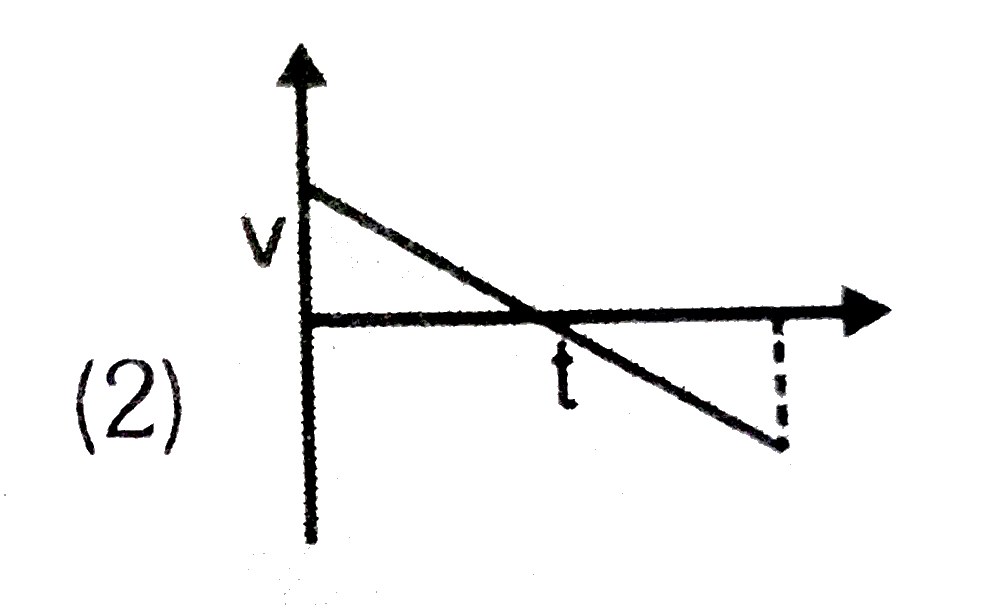 C
C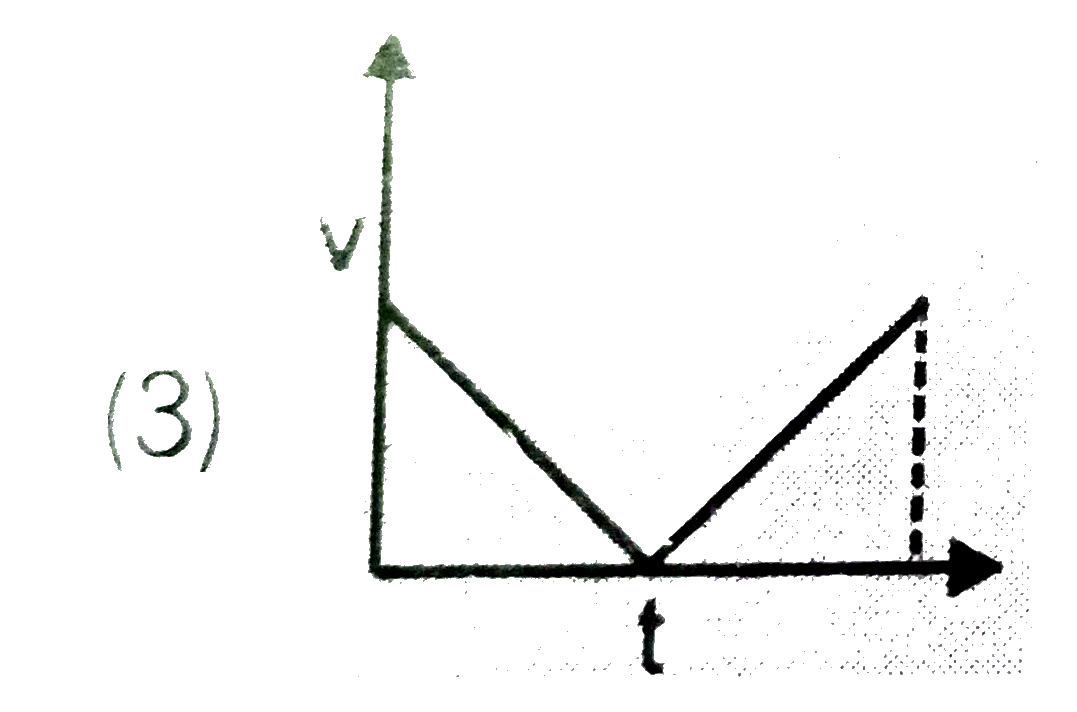 D
D
A body projected from the surface of the earth attains a height equal to the radius of the earth. The velocity with which the body was projected is
A√2GMRB√GMRC√3GMRD√5GM4R
A body attains a height equal to the radius of the earth. The velocity of the body with which it was projected is
View SolutionA body attains a height equal to the radius of the earth. the velocity of the body with which is was projected is
View SolutionA body is to be projected vertically upwards from earth's surface to reach a height of 9R, where R is the radius of earth. What is the velocity required to do so? Given g=10ms−2 and radius of earth=6.4×106m.
View SolutionA body projected vertically from the earth reaches a height equal to earth.s radius before returning to the earth. The power exerted by the gravitational force is greatest
View SolutionA body projected vertically from the earth reaches a height equal to earth’s radius before returning to the earth. The power exerted by the gravitational forces is greatest.
View Solution
