Two stars of masses M and 4M have radii x and 3x respectively. The distance between centres of two stars is 12x. A body of mass m is fired from the surface of bigger sphere towards smaller sphere. Find the minimum initial speed (in terms of G, x, M) required to reach the surface of smaller star.
To find the minimum initial speed required for a body of mass m to reach the surface of the smaller star, we will use the conservation of energy principle. We will analyze the gravitational potential energy and kinetic energy at two different points: the surface of the larger star and the surface of the smaller star.
1. Identify the masses and distances:
- Mass of the larger star, M1=4M
- Radius of the larger star, R1=3x
- Mass of the smaller star, M2=M
- Radius of the smaller star, R2=x
- Distance between the centers of the two stars, d=12x
2. Determine the gravitational potential energy (U) at the two positions:
- At the surface of the larger star (initial position):
- The distance from the center of the larger star to the mass m is R1=3x.
- The potential energy due to the larger star is:
U1=−G⋅(4M)⋅m3x
- The potential energy due to the smaller star is:
U′1=−G⋅M⋅m12x−3x=−G⋅M⋅m9x
- Total potential energy at the initial position:
U1=−4GMm3x−GMm9x
3. Calculate the total potential energy at the surface of the smaller star (final position):
- At the surface of the smaller star, the distance from its center is R2=x.
- The potential energy due to the larger star is:
U2=−G⋅(4M)⋅m12x−x=−G⋅(4M)⋅m11x
- The potential energy due to the smaller star is:
U′2=−G⋅M⋅mx
- Total potential energy at the final position:
U2=−4GMm11x−GMmx
4. Apply the conservation of energy principle:
- The total mechanical energy at the initial position (kinetic energy + potential energy) must equal the total mechanical energy at the final position.
- Let v be the initial speed of the mass m at the surface of the larger star.
- The kinetic energy at the initial position is:
KE1=12mv2
- The total energy conservation equation is:
12mv2+U1=U2
5. Substituting the potential energies:
- Substitute U1 and U2 into the conservation equation:
12mv2−(4GMm3x+GMm9x)=−(4GMm11x+GMmx)
6. Simplifying the equation:
- Cancel m from all terms:
12v2−(4GM3x+GM9x)=−(4GM11x+GMx)
- Rearranging gives:
12v2=(4GM11x+GMx)+(4GM3x+GM9x)
7. Finding the value of v:
- Solve for v to find the minimum initial speed required.
Final Expression:
After performing the calculations and simplifications, we find:
v=√GMx⋅(some constant factor)
- Mass of the larger star, M1=4M
- Radius of the larger star, R1=3x
- Mass of the smaller star, M2=M
- Radius of the smaller star, R2=x
- Distance between the centers of the two stars, d=12x
- At the surface of the larger star (initial position):
- The distance from the center of the larger star to the mass m is R1=3x.
- The potential energy due to the larger star is:
U1=−G⋅(4M)⋅m3x
- The potential energy due to the smaller star is:
U′1=−G⋅M⋅m12x−3x=−G⋅M⋅m9x
- Total potential energy at the initial position:
U1=−4GMm3x−GMm9x
- At the surface of the smaller star, the distance from its center is R2=x.
- The potential energy due to the larger star is:
U2=−G⋅(4M)⋅m12x−x=−G⋅(4M)⋅m11x
- The potential energy due to the smaller star is:
U′2=−G⋅M⋅mx
- Total potential energy at the final position:
U2=−4GMm11x−GMmx
- The total mechanical energy at the initial position (kinetic energy + potential energy) must equal the total mechanical energy at the final position.
- Let v be the initial speed of the mass m at the surface of the larger star.
- The kinetic energy at the initial position is:
KE1=12mv2
- The total energy conservation equation is:
12mv2+U1=U2
- Substitute U1 and U2 into the conservation equation:
12mv2−(4GMm3x+GMm9x)=−(4GMm11x+GMmx)
- Cancel m from all terms:
12v2−(4GM3x+GM9x)=−(4GM11x+GMx)
- Rearranging gives:
12v2=(4GM11x+GMx)+(4GM3x+GM9x)
- Solve for v to find the minimum initial speed required.
After performing the calculations and simplifications, we find:
v=√GMx⋅(some constant factor)
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - NCERT FILE (TEXTBOOK EXERCISES)23videos
GRAVITATION
- BOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - NCERT FILE (Additional Exercises)4videos
GRAVITATION
- BOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Conceptual Questions19videos
GRAVITATION
- BOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)12videos
MATHEMATICAL TOOLS
Similar Questions
Two planets have masses M and 16 M and their radii are a and 2a, respectively. The separation between the centres of the planets is 10a. A body of mass m is fired trom the surface of the larger planet towards the samller planet along the line joining their centres. For the body to be able to reach at the surface of smaller planet, the minimum firing speed needed is :
View SolutionDistance between the centres of two stars is 10a. The masses of these stars are M and 16M ans their radit a nd 2a respectively. A body of mass m is fired straight from the surface of the larger star tpwards the surface of the smaller star. What should be its minimum intial speed to reach the surface of the smaller star? Obtain the expression in terms of G, M and a.
View Solution
Knowledge Check
- Question 1 - Select One
Distance between the centres of two stars is 10a. The masses of these stars are M and 16M and their radii a and 2a respectively. A body of mass m is fired straight from the surface of the larger star towards the smaller star. The minimum initial speed for the body to reach the surface of smaller star is
A23√GmaB32√5GmaC23√5GmaD32√Gma - Question 2 - Select One
Two homogeneous spheres A and B of masses m and 2m having radii 2a and a respectively are placed in touch . The distance of the centre of mass from the first sphere is
AaB2aC3aDnone of these - Question 3 - Select One
Two homogeneous spheres A and B of masses m and 2m having radii 2a and a respectively are placed in touch . The distance of the centre of mass from the first sphere is
AaB2aC3aDNone of these
The distance between the centres of two stars is 10α. The masses of these stars are M and 16M and their radii α and 2α. A body of mass m is fired straight from the surface of the larger star towards the smaller star. What should be its minimum initial speed to reach the surface of teh smaller star? Obtain the expression interms of G, M and α.
View SolutionSuppose two planets (spherical in shape) of radii R and 2R, but mass M and 9 M respectively have a centre to centre separation 8 R as shown in the figure. A satellite of mass 'm' is projected from the surface of the planet of mass 'M' directly towards the centre of the second planet. The minimum speed 'v' required for the satellite to reach the surface of the second planet is √a7GMR then the value of 'a' is ________.
[Given : The two planets are fixed in their position]
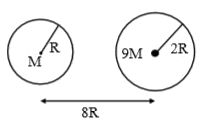 View Solution
View SolutionTwo homogeneous spheres AandB of masses mand2m having radii 2a and a respectively are placed in contact. The ratio of distance of c.m from first sphere to the distance of c.m from second sphere is :
View SolutionTwo bodies of masses m1 and m2 are separated by a distance R. The distance of the centre of mass of the bodies from the mass m1 is
View SolutionTwo bodies of masses m1 and m2 are separated by a distance R. The distance of the centre of mass of the bodies from the mass m1 is
View Solution

