A body is released from rest on the surface of water filled to a height of 2 m in a big cylinder. Assuming there is no viscous force, calculate of the time taken by the body to reach the bottom of cylinder. The relative density of body is 6.
To solve the problem of calculating the time taken by a body to reach the bottom of a cylinder filled with water, we can follow these steps:
Step 1: Understand the Forces Acting on the Body
When the body is released from the surface of the water, two main forces act on it:
1. The weight of the body (downward force), Fg=mg
2. The buoyant force (upward force), Fb
Step 2: Calculate the Buoyant Force
The buoyant force can be calculated using Archimedes' principle:
Fb=density of water×volume of the body submerged×g
Let the density of water be ρw and the volume of the body be V. Thus,
Fb=ρwVg
Step 3: Determine the Mass of the Body
The mass of the body can be expressed as:
m=density of body×volume of the body=ρbV
Given that the relative density of the body is 6, we have:
ρb=6ρw
Step 4: Write the Equation of Motion
The net force acting on the body when it is submerged is:
Fnet=Fg−Fb=mg−Fb
Substituting the expressions for mg and Fb:
Fnet=ρbVg−ρwVg=Vg(ρb−ρw)
Step 5: Calculate the Acceleration
Using Newton's second law, F=ma:
ma=Vg(ρb−ρw)
Substituting m:
ρbVa=Vg(ρb−ρw)
Cancelling V (assuming V≠0):
a=g(ρb−ρwρb)
Step 6: Substitute the Values
Substituting ρb=6ρw:
a=g(6ρw−ρw6ρw)=g(5ρw6ρw)=5g6
Step 7: Use the Equation of Motion to Find Time
We need to find the time taken to travel a distance S=2m from rest. Using the equation:
S=ut+12at2
Since the initial velocity u=0:
2=0+12(5g6)t2
This simplifies to:
2=5g12t2
Step 8: Solve for Time t
Rearranging gives:
t2=2×125g=245g
Taking the square root:
t=√245g
Assuming g≈9.81m/s2:
t=√245×9.81≈√2449.05≈√0.489≈0.7s
Final Answer
The time taken by the body to reach the bottom of the cylinder is approximately 0.7 seconds.
---
When the body is released from the surface of the water, two main forces act on it:
1. The weight of the body (downward force), Fg=mg
2. The buoyant force (upward force), Fb
The buoyant force can be calculated using Archimedes' principle:
Fb=density of water×volume of the body submerged×g
Let the density of water be ρw and the volume of the body be V. Thus,
Fb=ρwVg
The mass of the body can be expressed as:
m=density of body×volume of the body=ρbV
Given that the relative density of the body is 6, we have:
ρb=6ρw
The net force acting on the body when it is submerged is:
Fnet=Fg−Fb=mg−Fb
Substituting the expressions for mg and Fb:
Fnet=ρbVg−ρwVg=Vg(ρb−ρw)
Using Newton's second law, F=ma:
ma=Vg(ρb−ρw)
Substituting m:
ρbVa=Vg(ρb−ρw)
Cancelling V (assuming V≠0):
a=g(ρb−ρwρb)
Substituting ρb=6ρw:
a=g(6ρw−ρw6ρw)=g(5ρw6ρw)=5g6
We need to find the time taken to travel a distance S=2m from rest. Using the equation:
S=ut+12at2
Since the initial velocity u=0:
2=0+12(5g6)t2
This simplifies to:
2=5g12t2
Rearranging gives:
t2=2×125g=245g
Taking the square root:
t=√245g
Assuming g≈9.81m/s2:
t=√245×9.81≈√2449.05≈√0.489≈0.7s
The time taken by the body to reach the bottom of the cylinder is approximately 0.7 seconds.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Revision Exercise (Very Short Answer Questions)
54 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Revision Exercise (Additional Questions)
3 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT (Short Answer Type Questions)
5 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
Similar Questions
A body is relased from the top of a building of height 19.6 m. Find the velocity with which the body hits the ground .
View SolutionA body is projected vertically upward from the surface of earth with a velocity sufficient to carry it to initially. Calculate the time taken by it to reach height h.
View Solution
Knowledge Check
A smooth inclined plane is inclined at an angle θ with the horizontal. A body starts from rest and slides down the inclined surface. The time taken by the body to reach the bottom is
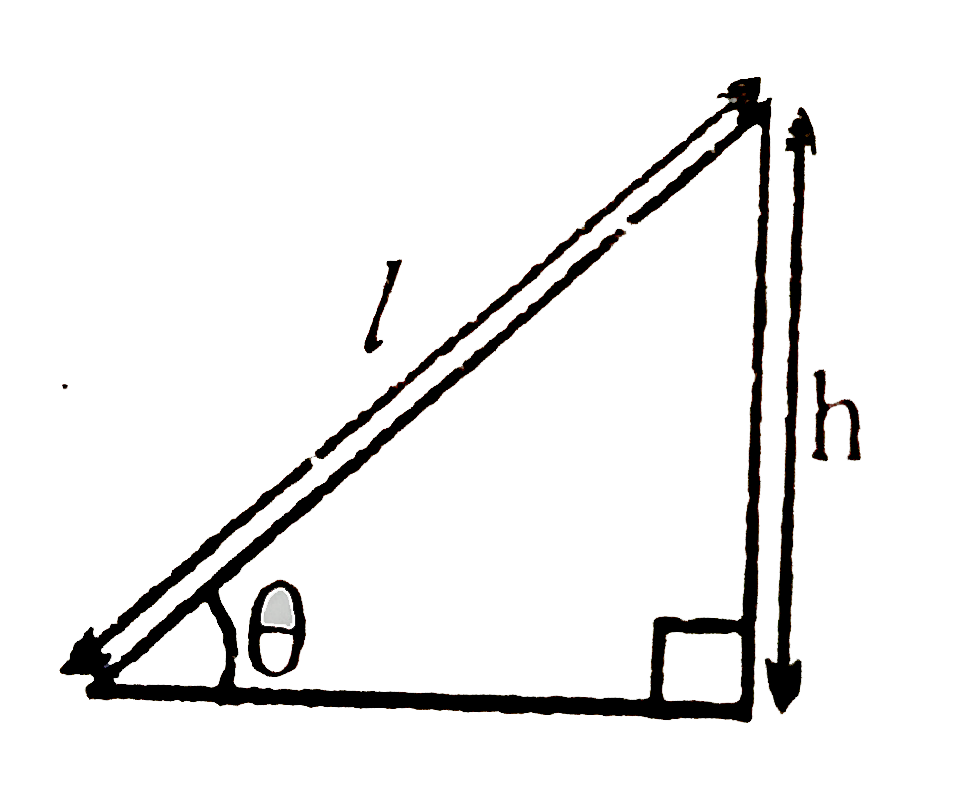 A√2hgB√2lgC√2lgsinθD1sinθ√h2g
A√2hgB√2lgC√2lgsinθD1sinθ√h2gA ball of relative density 0.8 falls into water from a height of 2 m. The depth to which the ball will sink is (neglect viscous forces)
A8 mB2 mC6 mD16 mA body is allowed to slide from the top along a smooth inclined plane of length 5m at an angle of inclination 30∘.If g=10ms−2, time taken by the body to reach the bottom of the plane is
A√32sB1.414sC1√2sD2s
A ball of relative density 0.8 falls into water from a height of 2 m. find the depth to which the ball will sink (neglect viscous forces)
View SolutionWhen a metallic sphere is released from the surface of water filled in a container of uniform area of cross section it is found to reach the bottom of the container in 2 s. If the density of the material of the sphere is 4.9gcm−3, calculate the pressure exerted by the liquid at the bottom of the container. Assume that only gravitational force and up-thrust act on the body.
View SolutionIf the body starts from rest from the top of the rough inclined plane of length 1, time taken to reach the bottom of the plane is
View SolutionBody A of mass M is dropped from a height of 1 m and body. B of mass 3M is dropped from a height of 9 m. The ratio of time taken by the bodies 1 and 2 to reach the ground is
View SolutionA stone of relative density K is released from rest on the surface of a lake. If viscous effects are lgnored, the stone sinks in water with an acceleration of
View Solution
